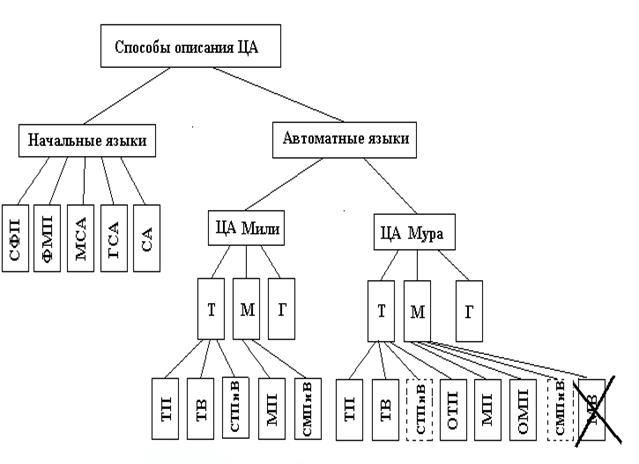
Начальные языки
Начальные языки трактуются как языки неявного задания ЦА или языки явного описания автомата на начальных этапах его рассмотрения. К таким языкам относятся: язык регулярных выражений алгебры событий, логическая схема алгоритма (ЛСА), графическая схема алгоритма (ГСА), матричная схема алгоритма (МСА), функциональная микропрограмма (ФМП), система формул перехода (СФП), входной, внутренний и выходной языки (алфавиты), законы функционирования.
СА, ГСА, МСА, ФМП и СФП подробно описаны в [11]. Тем не менее
они здесь в учебных целях кратко рассматриваются.
Рис.9. Классификация языков описания автоматов
2.1.1. Графическая схема алгоритма
Графическая схема алгоритма или граф-схема алгоритма (ГСА) является аналогом схемы алгоритма (СА), отличается от последней большей формализацией, несколько другим изображением блоков начала и конца.
Поскольку ГСА предложена для алгоритмов операций ЭВМ, то в ней нет средств для отражения ввода-вывода.
Вместо блоков в ГСА используются вершины: начальные Y0 , конечные Yк, операторные вершины Y1,Y2, … , условные вершины X1,X2, … .
На рис.10 показана СА классического алгоритма нахождения наиболь-
шего общего делителя (ННОД),
где: А и С - исходные числа,
НОД - наибольший общий делитель.
Видно, что заданные числа при А<С меняются местами (блоки 5¸7). По-
скольку после этого получается А >С, то число А заменяется на значение
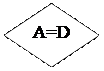
А - С. Подобные циклы повторяются до получения А= С (блоки 3¸8), число А и будет требуемым результатом (блок 9).
Имеются отличия применительно к условным вершинам. Прежде всего, условие (чаще всего отношение) записывается в закодированном виде.




 2
2
 | |||
 | |||

 3
3



 =
=

|
 ¹
¹

 4 >
4 >
 10
10
 |
 5 >
5 >

|
 11
11
 |
|
 7
7
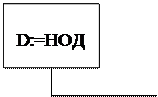 |
Рис. 10. СА ННОД чисел A и D
Если оно выполняется, то результату присваивается единичное значение, в противном случае - нулевое значение. С учетом этого выходы вершины отмечаются указанными значениями вместо “да” и “нет”.
Содержательная и закодированная граф-схемы алгоритмов представлены на рис.11 и 12 соответственно, коды микроопераций уi, микрокоманд Yi и условий XI - в табл.1.





y3

Y3
D: =НОД
Y0
 | |||||||
 | |||||||
 | |||||||
 | |||||||






|
|
|
 1 1 Y4
1 1 Y4
 |  | ||||||
 | |||||||
 | |||||||






|


|

 Y5
Y5


 1 1
1 1
 |
 0 0
0 0
|
| ||||
Y1 YK
y1
 | |||
 | |||
Y2
 | |||||
 | |||||
 |
Рис. 11. ГСА ННОД Рис.12. Закодированная ГСА ННОД
Таблица 1
| Коды | Микрооперация, условие | Коды | Микро- операция, условие | ||
| микро- операции, условия | микро- команды | микро- операции, условия | микро- команды | ||
| y1 y2 y3 | Y1 Y2 Y3 | НОД:=А А:=С С:=НОД | y4 X1 X2 | Y4 | A:=A-C A=C A>C |
Условия корректности ГСА похожи на условия корректности схемы алгоритма [14]:
1) у ГСА должна быть одна начальная и одна конечная вершины;
2) каждый выход соединен только с одним входом;
3) каждый вход соединен, по крайней мере, с одним выходом;
4) выходы условных вершин помечаются с помощью цифр “0” и “1”;
5) из начальной вершины должен быть путь к любой вершине;
6) из любой вершины должен быть путь в конечную вершину;
7) для любых наборов логических условий должен быть путь из началь-
ной вершины в конечную вершину.
2.1.2. Матричная схема алгоритма
Матричная схема алгоритма (МСА) представляет собой квадратную матрицу, строки которой соответствуют вершинам с выходами, столбцы - вершинам с входами. На пересечениях строк и столбцов записываются функции перехода. Такая функция представляет собой конъюнкцию кодов логических условий (логических переменных), переменная пишется без инверсии, если выход осуществляется по 1, в противном случае переменная пишется c инверсией. Функция перехода, равная 1, соответствует безусловному переходу.
Для указанного выше алгоритма МСА (МСА ННОД) представлена в табл.2
Таблица 2
| МСА ННОД | Y1 | Y2 | Y3 | Y4 | Y5 | YK |
| Y0, 4 | __ __ Х1Х2 | __ Х1Х2 | Х1 | |||
| Y1 | ||||||
| Y2 | ||||||
| Y3 | ||||||
| Y5 |
Для МСА можно сформировать условия корректности:
1) в МСА не должно быть строки Yk;
2) в МСА не должно быть столбца Y0;
3) должны быть столбец Yk и строка Y0;
4) не должно быть пустых строк и столбцов;
5) на строке не должно быть одинаковых функций перехода;
6) на строке не должно быть сочетаний 1 и функций перехода через логические переменные;
7) в столбце могут быть одинаковые функции перехода;
8) на строке может быть только одна 1;
9) дизъюнкция всех функций переходов на строке должна быть равна единице;
10) разные строки с одинаковыми функциями переходов разрешается оформ-
лять в одной строке с указанием всех индексов вершин старта.
По МСА можно упрощать алгоритмы и, следовательно, автоматы.
2.1.3. Функциональная микропрограмма
Функциональная микропрограмма (ФМП) операции представляет собой программу в терминах микроопераций и осведомительных сигналов.
Применительно к Ф - языку [9] ФМП имеет следующую структуру:
1) заголовок с ключевым словом “АЛГОРИТМ”;
2) совокупность описаний с ключевыми словами “ВХОДНЫЕ”, ”ВНУТРЕННИЕ”, ”ВЫХОДНЫЕ”;
3) НАЧАЛО;
4) тело;
5) окончание с ключевым словом “КОНЕЦ”.
ФМП алгоритма ННОД можно представить в следующем виде:
АЛГОРИТМ ННОД;
ВХОДНЫЕ А(1:32),С(1:32);
ВНУТРЕННИЕ: А(1:32),С(1:32),НОД(1:32);
ВЫХОДНЫЕ: НОД(1:32);
НАЧАЛО
М3: ПЕРЕЙТИ ЕСЛИ Х1 ТО М1;
ПЕРЕЙТИ ЕСЛИ Х2 ТО М2;
Y1;
Y2;
Y3;
М2: Y4;
ПЕРЕЙТИ М3;
М1: Y5;
КОНЕЦ.
По ФМП, как и по предыдущим способам описания, можно организовать алгоритмический процесс. Пусть А=8, С=6, тогда данный процесс следует отразить следующим образом:
начало;
1 цикл: 8=6, Х1=0, 8>6, X2=1, ®М2, Y4, А=2, В=6, ®М3;
2 цикл: 2=6, Х1=0, 2>6, Х2=0, Y1, НОД=2, А=6, В=2, А=4, ®М3;
3 цикл: 4=2, Х1=0, 4>2, X2=1, ®M2, Y4, A=2, B=2, ®M3;
4 цикл: 2=2, Х1=1, ®М1;
НОД=2;
конец.
Для исходных чисел 8 и 6 действительно наибольший общий делитель равен 2.
Для ФМП существуют и условия корректности:
1) должен быть заголовок;
2) данной меткой может быть помечен только один оператор (одна строка);
3) в операторах перехода могут использоваться одинаковые метки;
4) строка после оператора безусловного перехода должна иметь метку;
5) на строке может быть записана только одна микрокоманда или один оператор перехода.
2.1.4. Система формул переходов
Все переходы, соответствующие строке МСА, можно отразить в формуле переходов. Формул будет столько, сколько имеется строк в МСА. Получается система формул перехода (СФП).
Каждая формула переходов начинается с вершины, из которой рассматриваются переходы, в правой части формулы пишется дизъюнкция логических произведений вершин захода с соответствующими функциями перехода.
Между левой и правой частями формулы ставиться стрелка ® , которая отражает переходы от вершины левой части к одной из вершин правой части.
Переход совершается к той вершине, соответствующая функция перехода которой становится равной единице.
Для рассматриваемого алгоритма СФП включает в себя:
__ __ __
Y0,4 ® Х1Х2Y1+Х1Х2Y4+Х1Y5;
Y1 ® Y2;
Y2 ® Y3;
Y3 ® Y4;
Y5 ® YK.
Применительно к СФП можно сформулировать условия корректности:
1) не должно быть формулы перехода для Yк;
2) в правой части любой формулы не должно быть вершины Y0;
3) логическая сумма всех функций перехода любой формулы должна быть равна единице;
4) конъюнкция любой пары функций перехода формулы должна быть равна нулю;
5) в формуле не может быть одинаковых функций перехода;
6) у данной операторной вершины формул переходов может быть одинаковая функция перехода.
СФП позволяет производить формальные преобразования, упрощать алгоритм, следовательно, и автомат.
Дата добавления: 2015-07-18; просмотров: 1105;
