Автоматные языки
Автоматным языком считается такая совокупность, с помощью которой явно описывается автомат. К таким средствам относятся таблицы (Т), матрицы (М) и графы (Г).
Можно предложить следующую схему классификации этих языков, представленную на рис.9, где используются обозначения:
ТП - таблица переходов;
ТВ - таблица выходов;
СТП и В - совмещенная таблица переходов и выходов;
ОТП - отмеченная таблица переходов;
МП - матрица переходов;
МВ - матрица выходов;
СМП и В - совмещенная матрица переходов и выходов;
ОМП - отмеченная матрица переходов.
Из рис.9 следует, что для ЦА Мили и Мура могут использоваться и
одинаковые средства (ТП, ТВ, МП), и разные средства (СТП и В и ОТП; СМП и В и ОМП). Пунктирно обведенные средства использовать можно, но нецелесообразно. Зачеркнутое средство МВ является невозможным.
2.2.1. Таблицы переходов, выходов
Таблица переходов (ТП) - совокупность строк и столбцов, причем, строки соответствуют входным сигналам, а столбцы - предыдущим состояниям (ПС). Для ТП (табл. 3) на пересечениях фиксируются данные состояния, для таблицы выходов (ТВ) - выходные сигналы. Табл.4 является ТВ. Целесообразно данные средства рассмотреть для разных цифровых автоматов раздельно.
Пусть вначале будут ЦА Мили. Таблицы переходов, выходов и совмещенная таблица (СТП и В) представлены табл.3-5 соответственно.
Из табл. 3 и 4 следует, что множества входных сигналов Х, внутренних состояний S, выходных сигналов Y будут следующими:
Х= (x1 ,x2), S= (s1, s2, s3, s4), Y= (y1, y2, ,y3).
По табл.3 можно выполнить предусмотренные переходы:
если имеется предыдущее состояние s1 и действует входной сигнал x1, то получится новое (данное) состояние s2 (это можно отразить в виде s1, x1, s2), из состояния s1 под действием входного сигнала x2 автомат перейдет в состояние s3.
Из состояния s2 под действием входного сигнала x1 автомат перейдет в состояние s4, а под действием входного сигнала x2 - в состояние s1.
Из состояния s3 под действием входного сигнала x1 автомат перейдет в состояние s2, а под действием - x2 автомат перейдет в состояние s3.
Из состояния s4 под действием входного сигнала x1 автомат перейдет в состояние s1, а под действием - x2 перейдет в состояние s1.
Таблица 3
ТП ЦА Мили
 ПС
ВС ПС
ВС
| s1 | s2 | s3 | S4 |
| x1 | s2 | s4 | s2 | S4 |
| x2 | s3 | s1 | s3 | S1 |
Данным состояниям соответствуют логические выражения:
s1=s3 /\ x2; s2=(s1 \/ s3) /\ x1 \/ s2x2; s3=s1 /\ x2.
Особенностью ТП является то, что все пересечения ее заполнены. Если автомат имеет частичное описание, то какие-то пересечения могут быть пустыми. У пустого автомата все пересечения пусты. В ТП допускаются одинаковые элементы в строках и столбцах.
Таблица выходов аналогична таблице переходов, по ней определяются выходные сигналы:
y1=s1x1+(s3 \/ s2)x2; y2=s1x2; y3=(s2 \/ s3)x1.
Таблица 4
ТВ ЦА Мили
 |
| ПС ВС | s1 | s2 | s3 | s4 |
| x1 | у4 | y2 | y4 | y2 |
| x2 | y3 | y1 | y3 | y1 |
По данным ТП и ТВ можно составить совмещенную таблицу переходов и выходов, в которой на пересечениях в виде дроби фиксируются состояния и выходные сигналы (si / yj). СТП и В представляет собой табл.5.
Для ЦА Мура можно применять ТП (табл.6), ТВ (табл.7). Выходной сигнал автомата Мура соответствует данному состоянию (si / yi).
Таблица 5
СТП и В ЦА Мили
 ПС
ВС ПС
ВС
|  s1 s1
| s2 | s3 | s4 |
    x1 x1
| s2 у4 | s4 y2 | s2 y4 | s4 y2 |
   x2 x2
| s3 y3 | s1 y1 | s3 y3 | s1 y1 |
Таблица 6
ТП ЦА Мура
 |
| ПС ВС | s1 | s2 | s3 | s4 |
| x1 | s3 | s2 | s1 | s1 |
| x2 | s2 | s4 | s3 | s2 |
По данным ТП и ТВ автомата Мура также можно составить совмещенную таблицу переходов и выходов (табл.8), в которой на пересечениях в виде дроби фиксируются состояния и выходные сигналы (si / yi). Следовательно, в СТП и В этого автомата будут дублироваться индексы данных состояний для выходных сигналов.
Таблица 7
ТВ ЦА Мура
 ПС
ВС ПС
ВС
| s1 | s2 | s3 | s4 |
| x1 | у3 | y2 | y1 | y1 |
| x2 | y2 | y4 | y3 | y2 |
Экономнее эти дублирования отразить в верхней части столбцов (табл.9). Такая таблица называется отмеченной таблицей переходов (ОТП). Следовательно, СТП и В для ЦА Мура нецелесообразна. На рис. 9 она обведена пунктирно.
По таблицам ЦА Мура так же можно составить логические выражения для данных состояний, выходных сигналов и диаграммы его работы (рис.13).
Таблица 8
СТП и В ЦА Мура
 ПС
ВС ПС
ВС
| s1 | s2 | s3 | s4 |
     x1 x1
| s3 у3 | s2 y2 | s1 y1 | s1 y1 |
   x2 x2
| s2 y2 | s4 y4 | s3 y3 | s2 y2 |
Логические выражения имеют вид:
s1=(s4 \/ s5)x2; s2=(s2 \/ s3)x2 \/ s1x1; s3=(s4 \/ s5)x1; s4=s1x2; s5=(s2 \/ s3)x1;
y1=s1; y2=s2; y3=s3; y4=s4; y5=s5.
Пусть автомат Мили стартует с состояния s2, а автомат Мура – с состоя-
ния s4, последовательность входных сигналов для автомата Мили состоит из сигналов с номерами 2,1,1,1, а для автомата Мура - с номерами 2,1,1,2.
Таблица 9
ОТП
  ПС
ВС ПС
ВС
| s1 y1 | s2 y2 | s3 y3 | s4 y4 |
| x1 | s3 | s2 | s1 | s1 |
| x2 | s2 | s4 | s3 | s2 |
Диаграммы работы ЦА Мили отражены на рис. 13, диаграммы работы ЦА Мура – на рис.14 соответственно.
Как видно, автомат Мили с учётом начального состояния s2 последовательно находился в состояниях s2, s1, s2, s4, s4 с выдачей сигналов y1, y4, y2, y2, а автомат Мура с учётом начального состояния s4 последовательно находился в состояниях s4, s2, s2, s2, s4 с выдачей сигналов y4, y2, y2, y2, y4.
Видно, что выходные сигналы автомата Мили носят импульсный характер, а автомата Мура - потенциальный.
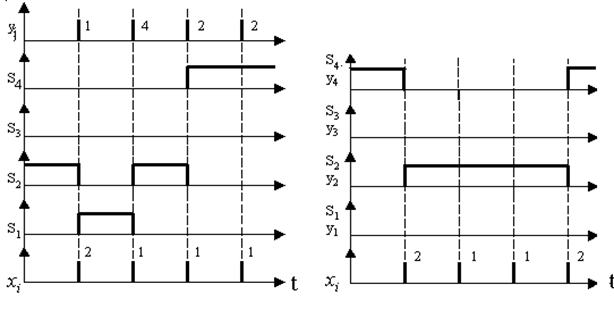
Рис.13. Диаграммы работы ЦА Мили Рис.14. Диаграммы работы ЦА Мура
2.2.2. Матрицы переходов, выходов
Матрицы в отличие от таблиц характеризуются однородностью обозна -чений строк и столбцов. Строки матриц соответствуют предыдущим состоя-
ниям (ПС), а столбцы - данным состояниям (ДС).
Матрицы переходов (МП) для обоих автоматов аналогичны, применительно к рассматриваемым примерам они должны иметь по 4 строки и по 4 столбца. На пересечениях МП размещаются входные сигналы.
Табл.10 является МП ЦА Мили , а табл.11 - МП ЦА Мура. Видно, что имеются пустые пересечения. В строке не могут использоваться одинаковые элементы. Этого ограничения нет для столбцов.
Очевидно, что чистой МВ для автоматов не получится, так как без входных сигналов xiматрица теряет смысл. Поэтому МВ на рис.9 зачеркнута.
Если в матрицах переходов автоматов Мили и Мура на пересечениях разместить и выходные сигналы (xi / yj и xi / yt), то получатся совмещенные матрицы переходов и выходов (СМП и В).
Такая матрица для ЦА Мили показана в табл.12. В ней по отношению к выходным сигналам никаких ограничений нет.
СМП и В для ЦА Мура представлена табл.13. Естественно, что в ней имеется ограничение на выходные сигналы: индексы у выходных сигналов в столбце являются одинаковыми, они совпадают с индексом данного состояния, соответствующему рассматриваемому столбцу.
Так фиксировать выходные сигналы не только нецелесообразно, но даже и некрасиво. С учетом этого СМП и В для ЦА Мура на рис.9 обведена пунктирно.
Поэтому для ЦА Мура целесообразна отмеченная матрица переходов (ОМП). Переходы в такой матрице фиксируются на пересечениях, а выходные сигналы - под обозначениями данных состояний в верхней части матрицы (табл.14).
Условия корректности отмеченной матрицы переходов по отношению к входным сигналам совпадают с условиями корректности СМП и В ЦА Мили.
Таблица 10
МП ЦА Мили
 ДС
ПС ДС
ПС
| s1 | s2 | s3 | s4 |
| s1 | x1 | x2 | ||
| s2 | x2 | x1 | ||
| s3 | x1 | x2 | ||
| s4 | x2 | x1 |
Таблица 11
МП ЦА Мура
 ДС
ПС ДС
ПС
| s1 | s2 | s3 | s4 |
| S1 | x2 | x1 | ||
| s2 | x1 | x2 | ||
| s3 | x1 | x2 | ||
| s4 | x1 | x2 |
2.2.3. Графы автоматов
Граф ЦА (ГА) - ориентированный граф, у которого в качестве вершин используются состояния, а в качестве дуг - переходы. В начале дуги фиксируется входной сигнал. Что касается выходного сигнала, то он для ЦА Мили ставится на конце дуги (рис.15), а для ЦА Мура внутри вершины (рис.16).
Таблица 12
СТП и В ЦА Мили
 ДС
ПС ДС
ПС
| s1 | s2 | s3 | s4 |
  s1 s1
| x1 y4 | x2 y3 | ||
   s2 s2
| x2 y1 | x1 y2 | ||
 s3 s3
| x1 y4 | x2 y3 | ||
  s4 s4
| x2 y1 | x1 y2 |
Таблица 13
СТП и В ЦА Мура
 ДС
ПС ДС
ПС
| s1 | s2 | s3 | s4 |
  s1 s1
| x2 y2 | x1 y3 | ||
    s2 s2
| x1 y2 | x2 y4 | ||
| s3 | x1 y1 | x2 y2 | ||
  s4 s4
| x1 y1 | x2 y2 |
Таблица 14
ОМП
  ДС
ПС ДС
ПС
| s1 y1 | s2 y2 | s3 y3 | s4 y4 |
| s1 | х2 | х1 | ||
| s2 | х1 | х2 | ||
| s3 | х1 | х2 | ||
| s4 | х1 | х2 |
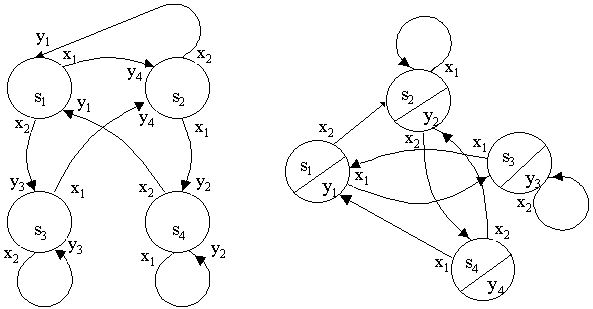 |
Рис.15. ГА Мили Рис.16. ГА Мура
Условия корректности для ГА Мили можно сформулировать следующим образом:
1) при выходе из данного состояния должны использоваться разные входные сигналы;
2) при заходе в данные состояния допускаются одинаковые входные сигналы;
3) при заходе в данное состояние разрешаются одинаковые выходные сигналы.
Условия корректности для ГА Мура являются не сколько другими:
1) при выходе из данного состояния должны использоваться разные входные сигналы;
2) при заходе в данные состояния могут использоваться одинаковые входные сигналы;
3) при заходе в данное состояние должны быть одинаковые выходные сигналы.
Можно заметить, что если в ЦА Мили при заходе в каждое состояние имеются одинаковые выходные сигналы, то такой ЦА можно легко преобразовать в автомат Мура. Что касается преобразования автомата Мура в автомат Мили, то для этого достаточно перенести выходные сигналы из вершин на концы дуг.
Дата добавления: 2015-07-18; просмотров: 1637;
