Оценка для математического ожидания и дисперсии

Если над некоторой случайной величиной X проведены испытания и получен ряд значений x₁, х₂, ...,x_n, то в качестве несмещенной и состоятельной оценки математического ожидания принимается среднее арифметическое из этих значений

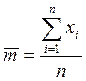
где 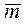— статистическое математическое ожидание. Эффективность или неэффективность оценки зависит от вида закона распределения случайной величины X. В теории вероятностей доказывается, что минимальная дисперсия Д будет иметь место при нормальном законе распределения случайной, величины X. При других законах распределения этого может и не быть.

В качестве состоятельной и несмещенной оценки для дисперсии принимается статистическая дисперсия, определяемая через второй начальный момент.

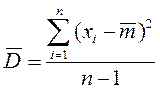
или

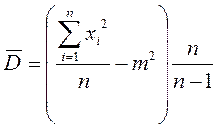
Оценка 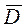для дисперсии не является эффективной. Она является асимптотически эффективной, т. е. при n → ∞ 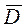→ D_min.