Окружной КПД осевой турбинной ступени

Под окружным КПД ступени понимается отношение работы на окружности к располагаемой работе

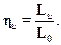
Для ступени с частичным использованием выходной энергии

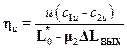, (15.1)

или

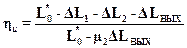. (15.2)

15.1. Окружной КПД активной турбинной ступени (р=0)

Предположим, что ступень работает без использования выходной энергии. В этом случае

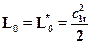. (15.3)

Работа на окружности ступени согласно выражению (14.2)

(15.4)

Знак "плюс" в последних двух равенствах поставлен по той причине, что проекция скорости w_2u направлена в сторону, противоположную направлению вращении рабочих лопаток.

Из треугольников скоростей . При ρ=0 отношение w₂/w₁=ψ, следовательно

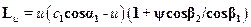
Таким образом, окружной КПД

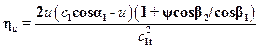. (15.5)

Так как C_1t=C₁/φ и, обозначая отношение скоростей u/C₁= 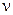₁, получим

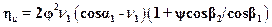. (15.6)

Отношение окружной скорости к скорости выхода потока из сопл ν₁ называется скоростной характеристикой турбинной ступени.

В активной турбинной ступен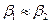и и 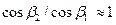. При этом функция 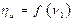имеет параболический характер. При v₁=0 и v₁=cosα₁ КПД ступени 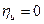. Отсюда следует, что при некотором значении v₁=v_1opt функция 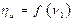имеет максимум.

Для определения оптимального значения характеристики, при которой 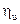достигает наибольшей величины, исследуем функцию 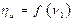на максимум

,

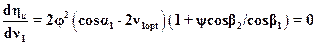из этого выражения следует

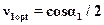(15.7)

При α₁=0 согласно формуле (15.7) v_1opt=0.5. В действительности α₁=8 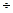25⁰, поэтому наибольшее значение 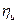активной ступени имеет место при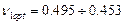

Наибольшее значение окружного КПД найдем, подставив выражение (15.7) в (15.6)

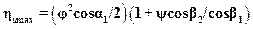. (15.8)

Графическая зависимость 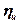от v₁ для турбинной ступени показана на рис.15.1.

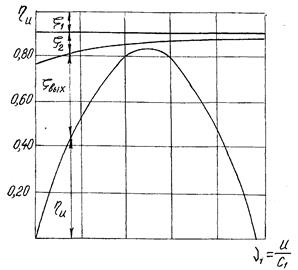
Рис.15.1 Зависимость окружного КПД активной ступени от скоростной характеристики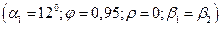

Указанные кривые построены при условии, что каждому значению 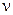₁ соответствует свой профиль рабочих лопаток с углом , обеспечивающий безударный вход на рабочую решетку, В связи с этим, приведенная на рис.15.1 зависимость 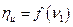будет отличаться от аналогичной зависимости, которую можно получить при испытании турбины.

Выразим окружной КПД через располагаемую работу ступени и потери на окружности колеса. Учитывая формулу (14.10), получим

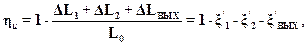(15.8)

где 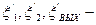относительные потери энергии соответственно в сопловом и рабочем аппаратах и с выходной скоростью.

15.2. Окружной КПД реактивной турбинной ступени (р=0.5)

В направляющей и рабочей решетках ступени благодаря равенству теплоперепадов L₀₁=L₀₂ применяют лопатки одного и того же профиля. Ступени с одинаковыми профилями лопаток в решетках называются конгруэнтными. В силу идентичности профилей в конгруэнтных ступенях имеет место равенство углов 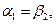и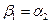

Если принять, что скорости потока при входе в направляющую и рабочую решетки одинаковы (C₀=W₁), что примерно имеет место в промежуточных ступенях реактивной турбины, то при одинаковых теплоперепадах в решетках будут равны и скорости выхода потока (С₁=W₂). Из треугольников скоростей следует, что W₁=C₂. Окружную работу турбинной ступени представим в следующем виде:

.

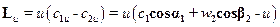Так как C₁=W₂; α₁=β₂

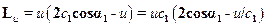. (15.9)

Располагаемая работа реактивной ступени работающей без использования выходной энергии

.

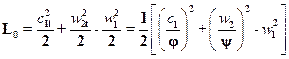Учитывая идентичность профилей направляющих и рабочих лопаток можно принять 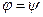, тогда

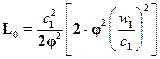. (15.10)

Из треугольника скоростей ,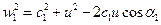

.

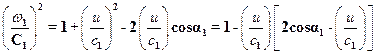Следовательно

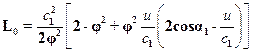
Таким образом, окружной КПД ступени можно выразить формулой

.

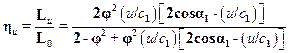Обозначая (u/С₁)=v₁, получим

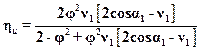. (15.11)

Из формулы (15.11) следует, что окружной КПД реактивной ступени зависит от тех же величин, что и КПД активной ступени.

Взяв производную от функции 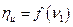и решив уравнение 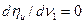, найдем, что максимум 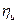ступени с ρ=0.5 будет при отношении скоростей

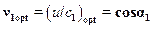. (15.12)

Таким образом, оптимальная характеристика реактивной ступени в два раза больше, чем активная. Если α₁=8…25°,то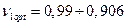

Подставляя в формулу (15.11) вместо v₁ оптимальную характеристику 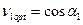, получим формулу для определения наибольшего КПД реактивной ступени

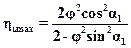. (15.13)

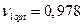Для частного случая, когда α₁=12°, , имеем и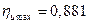

Для ступени с произвольной степенью реактивности оптимальное значение характеристикиv_1opt можно найти по приближенной формуле, полученной из условия осевого выхода потока и равенства осевых скоростей при входе в рабочую решетку и выходе из нее

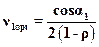. (15.14)