Силовое воздействие потока на рабочие лопатки

Действительная работа турбинной ступени из-за наличия потерь меньше теоретической.

Для того, чтобы найти действительную работу, совершаемую рабочей средой, определим, силу, с которой поток действует на рабочие лопатки при их обтекании. Рассмотрим осевую ступень с полным впуском.

Для определения силового воздействия потока на рабочие лопатки ступени применим закон количества движения, согласно которому векторная производная по времени от главного вектора количества движения системы равна главному вектору внешних сил, приложенных к системе

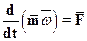, (13.1)

где 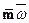- вектор количества движения;

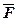- главный вектор внешних сил.

Выделим в потоке область abсd (рис.13.1), ограниченную двумя линиями аd и dс, совпадающими с линиями тока и находящимися на расстоянии шага t_p друг от друга, и линиями ab и dc, параллельными фронту решетки. Выделенная область охватывает один из профилей рабочей решетки. Предположим, что фронтальные ab и dc удалены

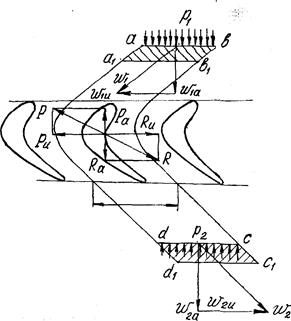
Рис.13.1 Силовое воздействие потока на рабочие лопатки осевой турбинной ступени.

от решетки настолько, что поля скоростей и давлений в сечениях ab и dc являются равномерными. Определим, как изменится количество движения массы рабочей среды, находящейся в пределах выделенной области abсd за время dt.

За рассматриваемый промежуток времени поток переместится в направлении оси межлопаточного канала и займет положение, ограниченное областью a₁b₁с₁d₁. Так как количество движения массы рабочей среды, находящейся в промежуточной области a₁b₁с₁d₁ за рассматриваемый период не меняется, то изменение количества движения всей выделенной массы будет равно разности количества движения массы 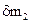, находящейся в области dcc₁d₁ и массы 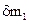, ограниченной областью abb₁a₁. Если режим движения рабочей среды установившийся и принимая расход через боковые границы выделенной области равным нулю, то 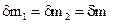. Таким образом, изменение количества движения массы рабочей среды, находящейся в пределах области abcd за время dt

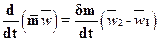, (13.2)

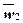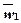где и - вектор скоростей масс соответственно 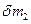и .

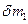Учитывая бесконечно малый промежуток времени dt, указанные векторы скорости равны векторам скорости в сечениях cd и ab.

Изменение количества движения произошло под действием внешних сил, приложенных к выделенной массе рабочей среды. Применительно к рассматриваемому потоку внешними силами будут реакция R со стороны поверхности обтекаемого профиля и силы давлений на торцевых поверхностях потока в сечениях ab и cd. Так как давление в сходственных точках линий тока ad и bс одинаковые, то результирующие силы давлений на боковых поверхностях, совпадающих с линиями тока будут равны и направлены в разные стороны. На изменение количества движения эти силы влияния оказывать не будут.

Сила реакции профиляR равна и противоположна по направлению силе Р, с которой поток действует на рабочую лопатку (R= -P). Раскладывая векторы сил Rи Р на окружные и осевые составляющие имеем:

Ru =-Рu, Rа =-Ра.

Для определения окружной составляющей силы Ри действия потока на рабочую лопатку напишем уравнение количества движения в проекции на окружное направление

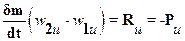, (13.3)

где w_1u и w_2u - проекции относительных скоростей соответственно при входе и выходе на окружное направление.

Если G - расход рабочей среды, a z_p - число рабочих лопаток, то

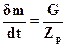, (13.4)

где 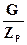- масса рабочей среды, протекающей через рабочий канал в единицу времени.

Учитывая (13.4) уравнение (13.3) можно переписать в виде

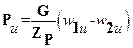. (13.5)

Сила Pu приложена к единичной лопатке. Суммарная сила, действующая на окружности и приложенная ко всем рабочим лопаткам, будет в z_p раз больше

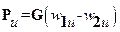. (13.6)

Стоящая в скобках разность скоростей является алгебраической, поэтому при определении силы Рu необходимо учитывать направление скоростей W_1u иW_2u. Зa положительное принимается направление скоростей, совпадающее с направлением движения рабочих лопаток. В турбинных ступенях скорость W_2u обычно является отрицательной, поэтому отрезки скоростей W_1u и W_2u следует суммировать (рис.13.2)

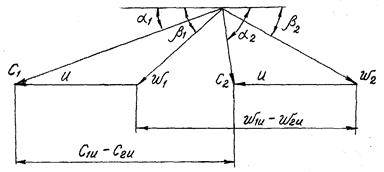
Рис.13.2 Треугольники скоростей осевой турбинной ступени

Из треугольников скоростей следует, что в осевой турбинной ступени при u₁=u₂=u разность проекций относительных скоростей на окружное направление равно разности проекций на то же направление абсолютных скоростей

,

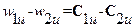поэтому будет справедливо

. (13.7)

Для определения осевой составляющей силыРа действия потока на лопатку уравнение количества движения напишем в проекции на осевое направление. Учитывая, что в осевом направлении на поток, кроме силы реакции Ra, действует разность давлений на торцевых поверхностях в сечениях аb и dc. имеем

,

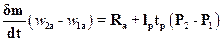где W_2a и W_1a- проекции относительных скоростей соответственно за решеткой и перед ней на осевое направление;

1р и tp - соответственно высота лопатки и шаг рабочей решетки.

Заменяя δm/dt, как было сделано выше, и учитывая, что Ra = -Ра, подучим для единичной лопатки

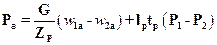. (13.8)

Суммарная сила действия потока на рабочие лопатки

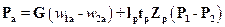. (13.9)

Учитывая равенство скоростей w_1a=C_1a и w_2a=C_2a, получим

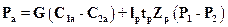. (13.10)

Осевая сила Ра воспринимается упорным подшипником турбины. Полученные для сил Рu и Ра формулы носят название формул Эйлера.