Форматы данных. Формы представления чисел в ЭВМ
Машинные команды оперируют данными, которые принято называть операндами. К наиболее общим (базовым) типам операндов можно отнести: адреса, числа, символы и логические данные. Помимо них ВМ обеспечивает обработку и более сложных информационных единиц: графических изображений, аудио-, видео- и анимационной информации. Такая информация является производной от базовых типов данных и хранится в виде файлов на внешних запоминающих устройствах. Для каждого типа данных в ВМ предусмотрены определенные форматы.
Среди цифровых данных можно выделить две группы:
- целые типы, используемые для представления целых чисел;
- вещественные типы для представления рациональных чисел.
В рамках первой группы имеется несколько форматов представления численной информации, зависящих от ее характера. Для представления вещественных чисел используется форма с плавающей запятой.
Числа в форме с фиксированной запятой
Представление числа X в форме с фиксированной запятой (ФЗ), которую иногда называют также естественной формой, включает в себя знак числа и его модуль в q-ичном коде. Здесь q – основание системы счисления или база. Для современных ВМ характерна двоичная система (q=2). Знак положительного числа кодируется двоичной цифрой 0, а знак отрицательного числа – цифрой 1.
Числам с ФЗ соответствует запись вида 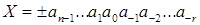 . Отрицательные числа обычно представляются в дополнительном коде. Разряд кода числа, в котором размещается знак, называется знаковым разрядом кода. Разряды, где располагаются значащие цифры числа, называются цифровыми разрядами кода. Знаковый разряд размещается левее старшего цифрового разряда. Положение запятой одинаково для всех чисел и в процессе решения задач не меняется. Хотя запятая и фиксируется, в коде числа она никак не выделяется, а только подразумевается. В общем случае разрядная сетка ВМ для размещения чисел в форме с ФЗ имеет вид, представленный на рис. 1.1, где n разрядов используются для записи целой части числа и r разрядов – для дробной части.
. Отрицательные числа обычно представляются в дополнительном коде. Разряд кода числа, в котором размещается знак, называется знаковым разрядом кода. Разряды, где располагаются значащие цифры числа, называются цифровыми разрядами кода. Знаковый разряд размещается левее старшего цифрового разряда. Положение запятой одинаково для всех чисел и в процессе решения задач не меняется. Хотя запятая и фиксируется, в коде числа она никак не выделяется, а только подразумевается. В общем случае разрядная сетка ВМ для размещения чисел в форме с ФЗ имеет вид, представленный на рис. 1.1, где n разрядов используются для записи целой части числа и r разрядов – для дробной части.
| Целая часть числа | Дробная часть числа | |||||||||
| qn-1 | q1 | q0 | q-1 | q-2 | q-r | |||||
| Знак | an-1 | ... | a1 | a0 | a-1 | a-2 | ... | a-r |
Рис. 1.1. Формат представления чисел с фиксированной запятой
При фиксации запятой перед старшим цифровым разрядом могут быть представлены только правильные дроби. Для ненулевых чисел возможны два варианта представления (нулевому значению соответствуют нули во всех разрядах): знаковое и беззнаковое. Фиксация запятой перед старшим разрядом встречалась в ряде машин второго поколения, но в настоящее время практически отжила свое.
При фиксации запятой после младшего разряда представимы лишь целые числа. Это наиболее распространенный способ, поэтому в дальнейшем понятие ФЗ будет связываться исключительно с целыми числами.
| Формат без знакового разряда | Формат со знаковым разрядом | |||||||||
| 2n-1 | 2n-2 | 21 | 20 | 2n-2 | 21 | 20 | ||||
| Знак | ||||||||||
| n-2 | n-1 | n-2 | n-1 |
Рис. 1.2. Представление целых чисел в формате Ф3
Представление чисел в формате ФЗ упрощает аппаратурную реализацию ВМ и сокращает время выполнения машинных операций, однако при решении задач необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты не выходили за допустимый диапазон формата, иначе возможно переполнение разрядной сетки и результат вычислений будет неверным.
Десятичные числа
В ряде задач, главным образом, учетно-статистического характера, приходится иметь дело с хранением, обработкой и пересылкой десятичной информации. Особенность таких задач состоит в том, что обрабатываемые числа могут состоять из различного и весьма большого количества десятичных цифр. Традиционные методы обработки с переводом исходных данных в двоичную систему счисления и обратным преобразованием результата зачастую сопряжены с существенными накладными расходами. По этой причине в ВМ применяются иные специальные формы представления десятичных данных. В их основу положен принцип кодирования каждой десятичной цифры эквивалентным двоичным числом из четырех битов (тетрадой), то есть так называемым двоично-десятичным кодом.
| Байт | Байт | Байт | Байт | |||||
| Зона | Цифра | Зона | Цифра | … | Зона | Цифра | Знак | Цифра |
а)
| Байт | Байт | Байт | Байт | |||||
| Цифра | Цифра | Цифра | Цифра | … | Цифра | Цифра | Цифра | Знак |
б)
Рис. 1.3. Форматы десятичных чисел: а – зонный; б – уплотненный
Используются два формата представления десятичных чисел (все числа рассматриваются как целые): зонный (распакованный) и уплотненный (упакованный). В обоих форматах каждая десятичная цифра представляется двоичной тетрадой, то есть заменяется двоично-десятичным кодом. Из оставшихся задействованных шести четырехразрядных двоичных комбинаций (24 = 16) две служат для кодирования знаков «+» и «–».
Зонный формат применяется в операциях ввода/вывода. В нем под каждую цифру выделяется один байт, где младшие четыре разряда отводятся под код цифры, а в старшую тетраду (поле зоны) записывается специальный код «зона», не совпадающий с кодами цифр и знаков.
При выполнении операций сложения и вычитания над десятичными числами обычно используется упакованный формат и в нем же получается результат (умножение и деление возможно только в зонном формате). В упакованном формате каждый байт содержит коды двух десятичных цифр. Правая тетрада последнего байта предназначается для записи знака числа. Десятичное число должно занимать целое количество байтов. Если это условие не выполняется, то четыре старших двоичных разряда левого байта заполняется нулями. Так, представление числа –7396 в коде ДКОИ и упакованном формате имеет вид, приведенный на рис. 1.4.
| Байт | Байт | Байт | |||
| Минус | |||||
Рис.1.4. Представление числа –7396 в упакованном формате
Размещение знака в младшем байте, как в зонном, так и в упакованном представлениях, позволяет задавать десятичные числа произвольной длины и передавать их в виде цепочки байтов. В этом случае знак указывает, что байт, в котором он содержится, является последним байтом данного числа, а следующий байт последовательности – это старший байт очередного числа.
Числа с плавающей запятой
От недостатков ФЗ в значительной степени свободна форма представления чисел с плавающей запятой (ПЗ), известная также под названиями нормальной или полулогарифмической формы. В данном варианте каждое число разбивается на две группы цифр. Первая группа цифр называется мантиссой, вторая – порядком. Число представляется в виде произведения 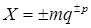 ,
,
где m – мантисса числа X,
р – порядок числа,
q – основание системы счисления.
Для представления числа в форме с ПЗ требуется задать знаки мантиссы и порядка, их модули в q-ичном коде, а также основание системы счисления. Нормальная форма неоднозначна, так как взаимное изменение m и p приводит к «плаванию» запятой, чем и обусловлено название этой формы.
| Модуль порядка | Модуль мантиссы | |||||||||||
| Знак m | Знак p | pr-1 | … | p1 | p0 | , | m-1 | m-2 | … | m-n | ||
Рис. 1.5. Форма представления чисел с плавающей запятой
Помимо разрядности порядка и мантиссы диапазон представления чисел зависит и от основания используемой системы счисления, которое может быть отличным от 2. Например, в универсальных ВМ (мэйнфреймах) фирмы IВМ используется база 16. Это позволяет при одинаковом количестве битов, отведенных под порядок, представлять числа в большем диапазоне. Так, если поле порядка равно 7 битам, максимальное значение qp, на которое умножается мантисса, равно 2128 (при q=2) или 16128 (при q=16), а диапазоны представления чисел соответственно составят 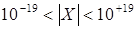 и
и 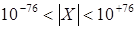 .
.
В большинстве вычислительных машин для упрощения операций над порядками последние приводят к целым положительным числам, применяя так называемый смещенный порядок. Для этого к истинному порядку добавляется целое положительное число – смещение. Например, в системе со смещением 128 порядок –3 представляется как 125 (–3 + 128). Обычно смещение выбирается равным половине представимого диапазона порядков. Отметим, что смещенный порядок занимает все биты поля порядка, в том числе и тот, который ранее использовался для записи знака порядка.
РСМ – машинный порядок, значение которого всегда положительно.
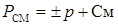 ,
,
где См – смещение, 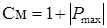 .
.
Рmax – максимальное значение порядка в пределах отведенного для него числа разрядов.
Если для изображения порядка отводится 6 разрядов и 1 разряд для изображения знака порядка, то

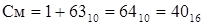
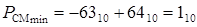

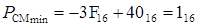
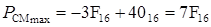
Таким образом PСМ может изменяться в пределах:
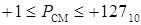 ;
;
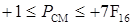 .
.
Для изображения смещенного порядка отводится 7 двоичных разрядов. Если значение смещенного порядка окажется равным нулю, то вырабатывается программное прерывание «Потеря порядка».
Следует отметить, что при изображении кода числа в памяти ЭВМ первые две старшие тетрады представляют совместно знак числа и смещенный порядок.
Мантисса в числах с ПЗ обычно представляется в нормализованной форме. Это означает, что на мантиссу налагаются такие условия, чтобы она по модулю была меньше единицы (|q| < 1), а первая цифра после точки отличалась от нуля. Полученная таким образом мантисса называется нормализованной.
Если первые i цифр мантиссы равны нулю, для нормализации ее нужно сдвинуть относительно запятой на i разрядов влево с одновременным уменьшением порядка на i единиц. В результате такой операции число не изменяется.
Рассмотренные принципы представления чисел с ПЗ поясним на примере. На рис. 1.6. представлен типичный 32-битовый формат числа с ПЗ. Старший (левый) бит содержит знак числа. Значение смещенного порядка хранится в разрядах с 1-го по 8-й. Третье поле слова содержит нормализованную мантиссу.
| Знак мантиссы | Смещенный порядок | Мантисса |
Рис. 1.6. Типичный 32–битовый формат числа с плавающей запятой
При выполнении в ЭВМ арифметических операций автоматически выполняются следующие действия над порядками:
а) При сложении и вычитании чисел предварительно выравниваются порядки. Для этого мантисса меньшего числа сдвигается вправо на число шестнадцатеричных разрядов, равное разности порядков чисел. При этом порядок меньшего числа увеличивается до порядка большего числа. Затем производится сложение (вычитание) мантисс. Полученное число нормализуется.
б) При умножении чисел их мантиссы перемножаются, а порядки складываются.
в) При делении мантисса делимого делится на мантиссу делителя, а из порядка делимого вычитается порядок делителя.
Знак результата при выполнении умножения (деления) определяется знаком произведения (частного) мантисс чисел, участвующих в операции.
Описанные процедуры завершаются приведением результата к нормализованной форме.
Арифметико-логическое устройство, работающее над числами с плавающей запятой должно иметь аппаратные средства для выполнения операций над мантиссами и порядками и вспомогательных операций (выравнивание порядков, нормализация и т.д.).
Дата добавления: 2015-07-18; просмотров: 3579;
