Процессы. 1.2. Случайные величины и процессы
1.2. Случайные величины и процессы
Существует класс случайных событий, имеющих числовые значения. Например, в опыте с игральной костью возможные результаты броска характеризуются числами 1,2,3,4,5,6. Принято говорить, что в подобных опытах наблюдаются случайные величины, а не случайные события. Роль случайных событий играют возможные значения случайной величины. Случайными величинами называются величины, которые в результате испытания могут принимать с определенными вероятностями те или иные заранее неизвестные возможные значения. В зависимости от того, какова мощность множества возможных значений случайной величины, различают дискретные и непрерывные случайные величины.
Дискретнойназывают случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно. При описании непрерывной случайной величины принципиально невозможно записать и пронумеровать все ее возможные значения, принадлежащие даже достаточно небольшому интервалу. Эти значения образуют бесконечное множество, которое называется континуум.
Теория случайных величин изучает вероятностные явления в статике, рассматривая их как некоторые зафиксированные результаты испытаний. Для описания процессов, которые отображают развивающиеся во времени, т.е. динамическиеслучайные явления, используются методы теории случайных процессов, которые также могут быть дискретными и непрерывными.
1.2.1. Дискретные случайные величины и процессы
Задание дискретной случайной величины.Для задания дискретной случайной величины недостаточно перечислить ее возможные значений, необходимо еще указать вероятности этих значений.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями дискретной случайной величины и их вероятностями. Его можно задать таблично или аналитически.
Например, таблица, характеризующая случайную величину X, генерируемую игральной костью
| xi | ||||||
| p(xi) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
где xi - возможные значения случайной величина X, а p(xi) - вероятность появления данных значений. При этом p1 + p2 + . . . + pn =1.
В дальнейшем случайные величины в отличие от их возможных значений будем обозначать большими латинскими буквами X, Y, ... .
Для иллюстрации аналитического задания распределения дискретной случайной величины X воспользуемся условиями, для которых получена формула Бернулли, рассматривая в качестве X число появления события А в этих испытаниях. Для нахождения закона распределения требуется определить возможные значения X и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, . . . , либо n раз. Таким образом, возможные значения X таковы: x0 = 0, x1 = 1, x2 = 2, . . ., xn = n.
Вероятности этих возможных значений могут быть вычислены по формуле Бернулли 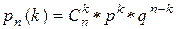 , где k=0,1,2, . . . , n. Эта формула и является аналитическим выражением искомого закона распределения. Это распределение, определяемое формулой Бернулли, называется биномиальным. Название объясняется тем, что правую часть этой формулы можно рассматривать как общий член разложения бинома Ньютона:
, где k=0,1,2, . . . , n. Эта формула и является аналитическим выражением искомого закона распределения. Это распределение, определяемое формулой Бернулли, называется биномиальным. Название объясняется тем, что правую часть этой формулы можно рассматривать как общий член разложения бинома Ньютона:
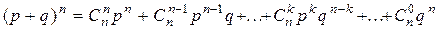 .
.
Первый член разложения определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях, второй - n-1 раз, последний член - событие не появится ни разу в n испытаниях.
Пользуясь аналогичными рассуждениями, можно получить аналитическое выражение для распределения Пуассона 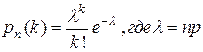 .
.
Числовые характеристики дискретных случайных величин. Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен, и приходиться ограничиваться менее подробным описанием в виде числовых характеристик случайных величин.
К числу важнейших числовых характеристик случайных величин относят математическое ожидание.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности, т.е.
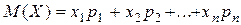 .
.
Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная постоянная величина.
Вероятностный смысл математического ожидания состоит в том, что оно приближенно (тем точнее, чем больше число испытаний) равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания:
а) математическое ожидание постоянной величины равно самой постоянной 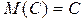 ;
;
б) постоянный множитель можно выносить за знак математического ожидания 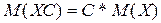 ;
;
в) математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий
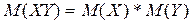 ;
;
г) математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий 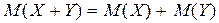 . Это свойство справедливо как для независимых, так и для зависимых случайных величин;
. Это свойство справедливо как для независимых, так и для зависимых случайных величин;
д) математическое ожидание числа появления события А в n независимых испытаниях равно произведению числа испытаний n на вероятность p появления события в каждом испытании, т.е. математическое ожидание биномиального распределения 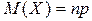 .
.
На практике часто требуется оценить рассеяние возможных значений случайной величин вокруг ее среднего значения. Отклонением называется разность между случайной величиной и ее математическим ожиданием, т.е. 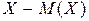 , но, поскольку математическое ожидание отклонения равно нулю т.е.
, но, поскольку математическое ожидание отклонения равно нулю т.е. 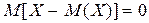 , то целесообразно заменить отклонения их квадратами. В результате получается следующая числовая характеристика случайной величины, называемая дисперсией и определяемая по формуле:
, то целесообразно заменить отклонения их квадратами. В результате получается следующая числовая характеристика случайной величины, называемая дисперсией и определяемая по формуле:
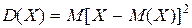 .
.
Таким образом, дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Пусть дискретная случайная величина задана законом распределения
| X | x1 | . . . | xn |
| p | p1 | . . . | pn |
Тогда квадраты отклонения будут иметь следующий закон распределения
| [X-M(X)]2 | [x1-M(X)]2 | . . . | [xn-M(X)]2 |
| p | p1 | . . . | pn |
И тогда по определению дисперсия равна
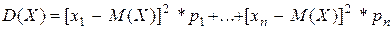 .
.
Однако более удобно пользоваться следующей формулой
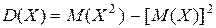 .
.
Свойства дисперсии:
а) дисперсия постоянной величины равна нулю 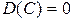 ;
;
б) постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат 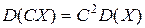 ;
;
в) дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин 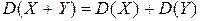 ;
;
г) дисперсия разности двух независимых случайных величин равна сумме их дисперсий 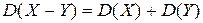 ;
;
д) дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний n на вероятность p появления и вероятность q непоявления события в одном испытании, т.е. дисперсия биномиального распределения 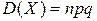 ;
;
е) дисперсия распределения Пуассона  ;
;
ж) квадратный корень из дисперсии случайной величины X называется среднеквадратическим отклонением случайной величины X 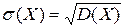 .
.
Свойства среднеквадратического отклонения случайной величины:
а) среднеквадратическое отклонение постоянной величины 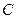 равно нулю
равно нулю 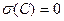 ;
;
б) при умножении случайной величины 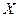 на постоянную
на постоянную 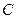 ее среднеквадратическое отклонение умножается на ту же постоянную
ее среднеквадратическое отклонение умножается на ту же постоянную 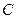 ;
;
в) среднеквадратическое отклонение суммы конечного числа попарно независимых случайных величин равно корню квадратному из суммы квадратов среднеквадратических отклонений этих величин 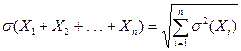
Многомерные дискретные случайные величины
До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие случайные величины называются одномерными.
Если возможные значения случайных величин определяются двумя, тремя, . . . n числами, то их называют двумерными, трехмерными, . . . n-мерными случайными величинами.
Законом распределения дискретной двумерной случайной величины (X,Y) называют перечень возможных значений этой величины, т.е. пар чисел (xi, yj) и их вероятностей p(xi, yj). Закон распределения может быть задан в виде таблицы.
| Y|X | x1 | . . . | xi | . . . | xn |
| y1 | p(x1,y1) | . . . | p(xi,y1) | . . . | p(xn,y1) |
| . . . | . . . | . . . | . . . | . . . | . . . |
| yj | p(x1,yj) | . . . | p(xi,yj) | . . . | p(xn,yj) |
| . . . | . . . | . . . | . . . | . . . | . . . |
| ym | p(x1,ym) | . . . | p(xi,ym) | . . . | p(xn,ym) |
Так как события (X=xi ,Y=yi) при i=1,2, . . ., n и j=1,2, . . . , m образуют полную группу событий, то сумма вероятностей во всех клетках таблицы равна 1. Вероятность того, что X примет значение xi равна сумме вероятностей в i-м столбце. Аналогично вероятность того, что Y примет значение yj равна сумме вероятностей в j-й строке.
Для того чтобы охарактеризовать зависимость между составляющими двумерной случайной величины вводится понятие условного распределения. Условным распределением, например, составляющей X при Y=yj называется совокупность условных вероятностей 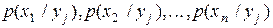 , вычисленных в предположении, что событие Y=yj уже наступило.
, вычисленных в предположении, что событие Y=yj уже наступило.
Важнейшей характеристикой условного распределения является условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины X при Y=y, где y - определенное возможное значение Y, называют произведение возможных значений X на их условные вероятности
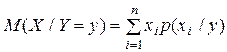 .
.
Для описания системы двух случайных величин, кроме математического ожидания и дисперсий составляющих, используются и другие характеристики, к которым, прежде всего, относятся корреляционный момент и коэффициент корреляции.
Корреляционным моментом mxy случайных величин X и Y называют математическое ожидание произведения отклонений этих величин
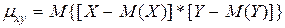 .
.
Для вычисления корреляционного момента можно пользоваться формулой:  .
.
Корреляционный момент двух независимых случайных величин X и Y равен 0.
Коэффициентом корреляции 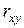 случайных величин X и Y называется отношение корреляционного момента к произведению среднеквадратических отклонений этих величин
случайных величин X и Y называется отношение корреляционного момента к произведению среднеквадратических отклонений этих величин 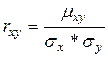 .
.
Две случайные величины X и Y называются некоррелированными, если их корреляционный момент равен 0. Две коррелированные величины так же и зависимы. Обратное не всегда имеет место, т.е. если две случайные величины X и Y зависимы, то они могут быть коррелированными и некоррелированными. Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя сделать заключение о независимости этих величин.
Дискретные случайные процессы
Как было сказано ранее, сообщение является последовательностью дискретных элементов - символов или непрерывной функцией.
Адекватной математической моделью первого случая является дискретный случайный процесс с дискретным временем. Процессы такого типа часто называют дискретными случайными последовательностями или цепями Маркова.
Цепь Маркова характеризуется тем, что переход от состояния к состоянию возможен лишь в дискретные моменты времени t0, t1, t2 ... . При этом абсолютные значения моментов времени роли не играют. Поэтому часто временной параметр отождествляют с множеством индексов {0,1,2, ...} и тогда цепь Маркова имеет вид: X0, X1, X2 , ..., Xi , ... . Здесь Xi - случайная величина, принимающая значения из множества L = {1,2,3 ...}, i = 0,1,2, .... - моменты времени.
Дата добавления: 2015-07-14; просмотров: 1682;
