Описание и организация выбора
Задача выбора возникает, когда из некоторого конечного или бесконечного множества надо отобрать подмножество в каком-то смысле хороших элементов.
Пусть Х – исходное множество альтернатив. Подмножество отбираемых элементов называется выбором, и обозначается С(Х) (от английского choice –выбор). Алгоритм, реализующий этот отбор, называется механизмом выбора.
Рассмотрим примеры наиболее распространенных механизмов выбора.
1) Скалярный оптимизирующий механизм – выбор вариантов, при которых некоторая скалярная функция f(х) достигает максимума
Сопт(Х) = { хÎХ | х = arg max f(x) }
2) Условно-оптимальный механизм – выбор по схеме математического программирования, т.е. выбор таких хÎХ, при которых достигается условный максимум скалярной функции f0(x) при выполнении системы ограничений
Смп(Х) = { хÎХ | х = arg max f0(x) | f i(х) £ 0, i = 1,.., m] }.
Перечисленные механизмы базируются, как нетрудно догадаться, на критериальном языке описания выбора. Следующие два механизма основаны на использовании языка бинарных отношений.
3) Механизм доминирования по бинарному отношению R – выбор тех хÎХ, которые с любым элементом из Х находится в отношении R (элемент х лучше любого y в смысле отношения предпочтении R)
СR(Х) ={ хÎХ | " yÎХ : (x, y)ÎR }
4) Механизм блокировки по бинарному отношению R – выбор тех элементов xÎX, для которых в Х нет элемента лучше в смысле отношения предпочтения R
СR(Х) = { хÎХ | " yÎХ : (y, х)ÏR }.
Приведем несколько теорем о свойствах выбора.
Теорема 4.1. Пусть имеем два отношения R1 и R2, такие, что R2 = (R1)d. Тогда а) СR1(Х) = СR2(Х) и б) СR1(Х) = СR2(Х).
Доказательство. Пусть х Î СR2(Х). По определению СR2(Х) = { хÎХ | " yÎХ : (y, х)ÏR2 }. Пусть (y, х)ÏR2 =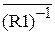 
. Это означает, что (у, х) Î(R1)–1 , или (х, у) ÎR1. Так как последнее соотношение выполняется для любого у ÎХ, то значит х Î СR1(Х). Следовательно, СR2(Х) Í СR1(Х).
Обратное включение и свойство б) доказывается аналогично, т.к. для любого отношения R выполняется равенство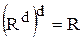 
.
На основании данной теоремы получаем, что свойства механизмов доминирования и блокировки во многом совпадают.
Приведем без доказательства также следующие теоремы о выборе.
Теорема 4.2. Бинарное отношение R порождает непустой выбор (т.е. содержащий хотя бы один элемент), основанный на механизме доминирования или блокировки тогда и только тогда, когда R ациклично.
Теорема 4.3. Бинарное отношение R порождает однозначный выбор (т.е. содержащий ровно один элемент), основанный на механизме доминирования или блокировки тогда и только тогда, когда R ациклично и слабо полно.
Задание. Указать такое бинарное отношение, при котором механизм доминирования совпадает со скалярно-оптимизирующим механизмом выбора.
Дата добавления: 2015-08-26; просмотров: 791;