Теплоємність електронного газу. Звернемось до розподілу Фермі-Дірака при температурі, більшій за абсолютний нуль

Звернемось до розподілу Фермі-Дірака при температурі, більшій за абсолютний нуль. Графік залежності імовірності заповнення електронами квантових станів від енергії показано на рисунку (рис. 2.32)

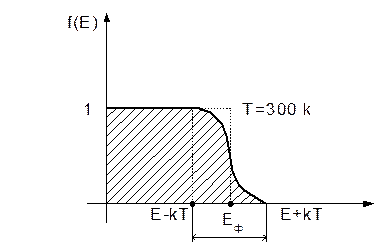
Рис. 2.32

З рисунка видно, що при нагріванні змінюють свою енергію лише ті електрони, які розміщені на енергетичних рівнях поблизу енергії Фермі. Кількість таких електронів досить невелика.

Частку електронів, які беруть участь у тепловому русі, можна оцінити співвідношенням 2кТ/Е_ф. Теплоємність одного моля електронного газу можна оцінити за допомогою класичного співвідношення

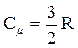, (2.6.20)

де R – універсальна газова стала.

Але приймаючи до уваги, що лише досить невелика частка електро-нів бере участь у тепловому русі, молярна теплоємність електронного газу буде дорівнювати

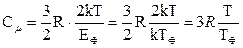, (2.6.21)

З урахуванням того, що для більшості металів 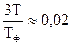, одержимо остаточне значення молярної теплоємності електронного газу в металі

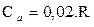. (2.6.22)

При звичайних температурах електронний газ в металі вносить досить незначний вклад в молярну теплоємність кристалу, яку можна визначити за законом Дюлонга і Пті (С_mк=3R).

Порівняємо ці теплоємності

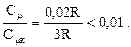(2.6.23)

Електронна теплоємність почне помітно впливати на загальну теплоємність металу при температурах, близьких до абсолютного нуля, точніше при температурах менших за q/50. Тут теплоємність кристалічної ґратки пропорційна Т³ буде меншою за електронну теплоємність, пропорційну Т.