Дифракційна решітка. Кутова дисперсія і роздільна здатність дифракційної решітки
Дифракційною решіткою називається оптичний прилад, який складається з великої кількості однакових щілин, розділених між собою однакової ширини непрозорими проміжками. Відстань d між серединами двох сусідніх щілин, називається сталою дифракційної решітки.
Якщо розмістити паралельно решітці збиральну лінзу, то в її фокальній площині на екрані можна буде спостерігати результати дифракції світла від решітки (рис.4).
Оптична різниця ходу променів від двох сусідніх щілин дорівнює
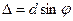 (21)
(21)
Оптична різниця фаз в цьому випадку буде дорівнювати
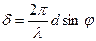 (22)
(22)
В точку P на екрані приходять промені від усіх щілин. Всі ці промені зсунуті за фазою на однакову величину 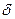 .
.
Для знаходження результуючої амплітуди всіх хвиль, які прийшли в точку Р слід скористатися формулою результуючої амплітуди при інтерференції багатьох хвиль
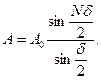 (23)
(23)
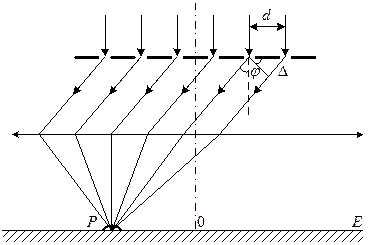
Рис. 4
З урахуванням (22) результуюча амплітуда 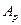 буде дорівнювати
буде дорівнювати
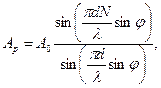 (24)
(24)
де 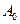 – амплітуда хвиль від однієї щілини;
– амплітуда хвиль від однієї щілини;
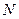 – число щілин у решітці;
– число щілин у решітці;
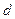 – стала дифракційної решітки;
– стала дифракційної решітки;
 – довжина хвилі монохроматичного світла.
– довжина хвилі монохроматичного світла.
Проведемо аналіз формули (24).
а) якщо вираз у знаменнику (24) досягає мінімуму, тобто буде дорівнювати нулю, то амплітуда 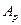 буде найбільшою. Ця умова є умовою максимуму дифракції на дифракційній решітці, тобто
буде найбільшою. Ця умова є умовою максимуму дифракції на дифракційній решітці, тобто
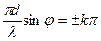 ,
,
звідки
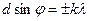 . (25)
. (25)
Формула (25) є умовою головних максимумів дифракції на дифракційній решітці.
б) побічні максимуми дифракції можна одержати, якщо чисельник у формулі (24) досягає максимуму. Це можливо за умови, коли
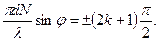 (26)
(26)
Після скорочення одержимо
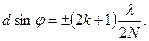 (27)
(27)
Вираз (27) є умовою побічних максимумів дифракції на дифракційній решітці.
в) побічні мінімуми дифракції на дифракційній решітці одержуємо із умови коли чисельник формули (25) буде найменшим, тобто коли
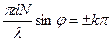 (28)
(28)
звідки
 . (29)
. (29)
Формула (29) є умовою побічних мінімумів на дифракційній решітці.
Дифракція світла на дифракційній решітці, яка має N щілин, показана на рис.5.
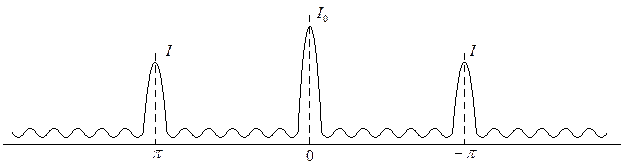
Рис.5
Розрахунки показують , що 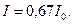 Для достатньо великих значень N побічні мінімуми і побічні максимуми не проявляються. Число головних максимумів дифракції визначається відношенням d до λ (
Для достатньо великих значень N побічні мінімуми і побічні максимуми не проявляються. Число головних максимумів дифракції визначається відношенням d до λ ( 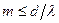 ), при цьому
), при цьому 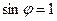 .
.
Важливо знати:
а) внаслідок немонохроматичності біле сонячне світло після проходження дифракційної решітки дає максимуми ІІ, ІІІ і більш високих порядків у вигляді спектрів.
б) хороша решітка з малим d і великим N дає дифракційні спектри з великою роздільною здатністю. Характерною ознакою дифракційних спектрів є рівномірний розподіл кольорів у спектрі. На відміну від дифракційного спектра, призматичний спектр стиснутий в області червоних кольорів і розширений в області фіолетових кольорів.
Кожна дифракційна решітка характеризується кутовою дисперсією, яка позначається буквою Д
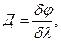 (30)
(30)
де 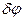 – кутова відстань між спектральними лініями, які відрізняються за довжиною хвилі на величину
– кутова відстань між спектральними лініями, які відрізняються за довжиною хвилі на величину 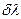 .
.
Для знаходження кутової дисперсії дифракційної решітки слід продиференціювати формулу головних максимумів дифракції  , тобто
, тобто
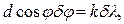
звідки
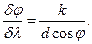
В межах невеликих кутів 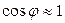 , тому можна вважати, що
, тому можна вважати, що
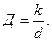 (31)
(31)
Таким чином кутова дисперсія обернено пропорційна періоду решітки d. Чим вищий порядок спектра k, тим більша дисперсія.
Роздільною здатністю спектрального приладу, а таким є дифракційна решітка, називають безрозмірну величину
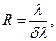 (32)
(32)
де R – роздільна здатність;
λ – довжина хвилі;
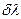 – мінімальна різниця довжин хвиль двох сусідніх спектральних ліній, при якій ці лінії спостерігаються роздільно, якщо виконується умова Релея.
– мінімальна різниця довжин хвиль двох сусідніх спектральних ліній, при якій ці лінії спостерігаються роздільно, якщо виконується умова Релея.
Згідно з умовою Релея дві спектральні лінії будуть видимі роздільно у випадку, коли мінімум другої спектральної лінії знаходиться не ближче максимуму першої лінії (рис.6).
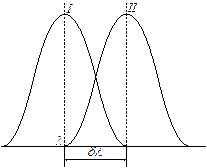
Рис.6
Знайдемо роздільну здатність дифракційної решітки. За умовою Релея максимум першої лінії в крайньому випадку збігається з мінімумом другої спектральної лінії. Якщо спектральні лінії будуть розміщені ближче ніж 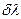 , то жоден спектральний прилад розділити їх не зможе.
, то жоден спектральний прилад розділити їх не зможе.
Запишемо умову головного максимуму для другої спектральної лінії
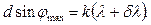 (33)
(33)
Умова першого побічного мінімуму для другої лінії
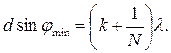 (34)
(34)
Оскільки ліві частини однакові, то прирівняємо праві частини цих рівнянь
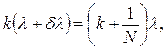
або
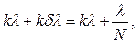
звідки
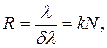
де 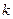 – порядок спектра;
– порядок спектра;
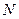 – число всіх щілин у решітці.
– число всіх щілин у решітці.
Дата добавления: 2015-08-26; просмотров: 1335;
