Обратная засечка (задача Потенота)
Сущность обратной засечки заключается в определении положения четвертого пункта (точки стояния) по трем исходным. Эта задача встречается при создании съёмочных сетей, привязке аэрофотоснимков, выносе проектов в натуру и других случаях.
Для ее решения предложено много аналитических и графических способов. При аналитическом способе задаются координаты трех исходных пунктов и измеренные углы или направления на определяемом пункте.
На основе трех исходных пунктов задача решается без контроля правильности измерения углов и выборки исходных данных. Поэтому на практике используют четыре исходных пункта.
Точность определения положения пункта обратной засечкой зависит от ошибок измерения углов, ошибок исходных данных и взаимного расположения пунктов. Если определяемый пункт находится вблизи окружности, проходящей через исходные пункты, то задача решается грубо. В связи с этим обратную засечку рекомендуется делать с предвычислением точности.
В учебнике [1, §162] приводится решение обратной засечки с использованием формул Кнейссля, однако она требует графических построений или дополнительных расчетов.
Приведем вывод формул, которые позволяют решить задачу с оценкой точности без графических построений.
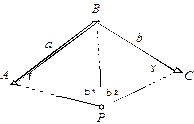Рис. 2.22.
| Даны координаты пунктов А, B, C. Измерены углы β1, β2 (рис. 2.22). Требуется определить координаты точки P (X, Y). В начале решением обратных геодезических задач определим дирекционные углы и длины исходных линий: |
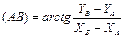, (26)
(27)
, (28)
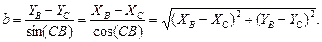(29)
Далее задача сводится к определению углов φ и ψ. Определим полусумму углов φ и ψ, которую обозначим как А
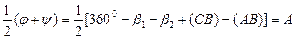. (30)
Определим полуразность этих углов, которую обозначим через В
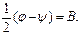(31)
Определим диаметры описанных окружностей около треугольников ABP и BCP:
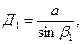
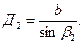(32)
Выразим сторону ВР через Д1, Д2 и углы φ и ψ.
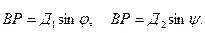(33)
Откуда
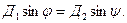
Разделив две части этого равенства на Д1sin ψ, получим
.
Образуем пропорцию и введем обозначение N:
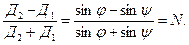(34)
С учетом (32)
(35)
С учетом тригонометрических формул
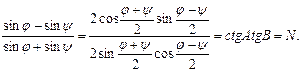
Отсюда
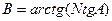. (36)
Вычислив значения А и В, определим углы φ и ψ
φ = А+ В, (37)
ψ = А – В. (38)
Далее определим длину линии АР
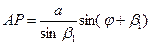(39)
и координаты точки Р:
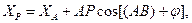(40)
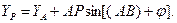(41)
Таким образом, задача решается по формулам 26–41.
Для контроля координат точки Р можно вычислить второй раз, используя формулы
,
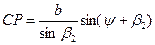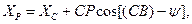
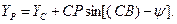
Среднюю квадратическую ошибку в положении пункта Р, определенного обратной засечкой, можно вычислить по формуле
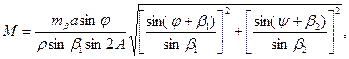(42)
где mβ – средняя квадратическая ошибка измерения углов β1 и β2.
Рассмотренная обратная засечка по трем исходным пунктам называется однократной. В таком виде она, как правило, не допускается, т.к. не контролируется правильность измерения углов и выписка исходных данных.
Для полного контроля наблюдается не 3, а минимум 4 пункта (рис. 2.23).
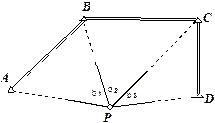
Рис. 2.23.
Задача решается дважды при различном сочетании исходных пунктов. Например, первый раз используются пункты А, В, С и второй раз пункты В, С, D. Для каждого варианта решения определяется средняя квадратическая ошибка положения пункта М по формуле (42). Ожидаемое среднее квадратическое значение Mr расхождения в положении пункта Р при двух решениях составит
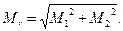
Отсюда допустимое расхождение в значениях вычисленных координат можно установить по формуле
где X/ , Y/ – координаты точки из первого решения;
X// , Y// – координаты точки из второго решения.
За окончательное значение координат пункта Р берут среднее арифметическое, которое будет иметь ошибку
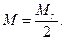
Дата добавления: 2015-08-26; просмотров: 5127;