Расчет короткого трубопровода

Коротким считается трубопровод, в котором потери на местных сопротивлениях превышают 5% от общих потерь. К коротким относятся системы водоснабжения, водоотведения, горячего водоснабжения внутри зданий (см. рис. 5.6 и 5.7).

Целью расчета короткого трубопровода может быть определение напора или давления в начале трубопровода, потерь напора или потерь давления, а также определение расхода или диаметра трубопровода при известном напоре в его начале.

При расчете напора в начале короткого трубопровода должны быть заданы:

• напор или давление в конце трубопровода;
• расход
• диаметр и длина трубопровода.

При расчете напора в конце короткого трубопровода должны быть заданы:

• напор или давление в начале трубопровода;
• расход;
• диаметр и длина трубопровода.

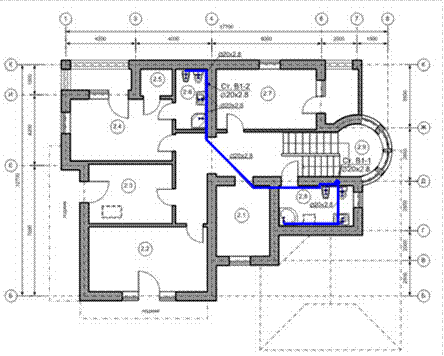
Рис. 5.6. Схема водоснабжения этажа

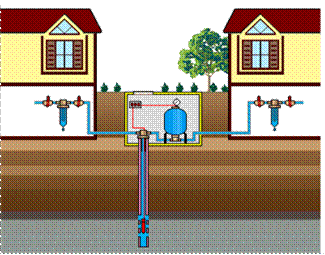
Рис. 5.7. Схема водоснабжения коттеджей

Если целью расчета является определение расхода трубопровода, то должны быть заданы:

• напор или давление в начале и в конце трубопровода;
• диаметр и длина трубопровода.

В тех случаях, когда необходимо подобрать диаметр трубопровода должны быть известны напоры (давление), расход и длина трубопровода. В этом случае задача решается подбором диаметра, соответствующего установленным условиям подачи жидкости.

При расчете коротких трубопроводов применяется уравнение Бернулли для двух выбранных сечений и уравнение неразрывности. Обычно расчетные сечения выбираются в начале и в конце трубопровода. Обязательным условием является то, что движение на расчетном участке трубопровода должно быть установившемся, а в расчетных сечениях в начале и в конце расчетных участков трубопровода – равномерным.

Уравнение Бернулли составляется относительно плоскости сравнения, которой может быть любая горизонтальная плоскость, в том числе линия горизонта, поверхность земли и т.д. Плоскость сравнения рекомендуется проводить с таким расчетом, чтобы упростить решение уравнения Бернулли. Обычно плоскость сравнения проводится или по центру трубы в начале или в конце трубопровода, или по уровню жидкости в резервуаре, из которого происходит истечение жидкости или куда она подается.

Расчет необходимо начать с определения формы записи уравнения Бернулли. Для расчета систем водоснабжения и водоотведения обычно применяется уравнение Бернулли в форме напоров:

.

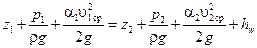(5.1)

Если известны расход и диаметр трубопровода, то вначале определяется режим движения жидкости для всех участков с различными средними скоростями движения жидкости. Режим движения жидкости считаем турбулентным, если число Рейнольдса больше или равно 2320, и ламинарным, если Re<2320. Если расход неизвестен, то в первом приближении для маловязких жидкостей (вода), режим движения принимается турбулентным, для вязких (густое индустриальное масло) – ламинарным. После определения расхода в первом приближении определяется число Рейнольдса и по нему уточняется режим движения.

Расчет трубопровода фактически сводится к расчету потерь – местных и по длине. В коротком трубопроводе потери напора по длине определяются по формуле:

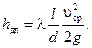
(5.2)

Если трубопровод имеет участки с разными диаметрами, то потери по длине определяются для каждого участка отдельно, а затем складываются. Коэффициент гидравлического трения λ определяется по формулам, которые выбираются в зависимости от режима движения и области сопротивления. При неизвестном расходе:

• для ламинарного режима коэффициент гидравлического трения определяется по формуле:

,

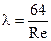(5.3)

а затем уточняется;

• для турбулентного режима коэффициент гидравлического трения рассчитывается по формуле:

.

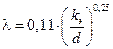(5.4)

а затем уточняется. Коэффициент эквивалентной шероховатости трубы определяется по таблицам в зависимости от материала трубы и времени ее эксплуатации.

Потери напора на местном сопротивлении при турбулентном режиме определяются по формуле:

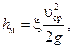
(5.5)

где 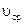– средняя скорость на участке после сопротивления.

Если режим движения ламинарный, то потери напора на местном сопротивлении определяются по формуле:

,

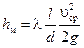(5.6)

где l – эквивалентная длина, определяемая по таблицам в зависимости от вида местного сопротивления.

После определения потерь напора на каждом местном сопротивлении, они складываются. Считается, что эти потери происходят в данном сечении трубопровода.

После расчета потерь напора по длине и на местных сопротивлениях строятся линии полного и пьезометрического напоров. Для этого трубопровод разбивается на сечения. Количество сечений зависит от количества прямолинейных участков трубопровода и местных сопротивлений. Полный напор в начальном сечении трубопровода определяется по формуле:

.

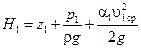(5.7)

В сечении с местным сопротивлением на графике указывается падение напора на величину местного сопротивления 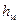. Обычно в этом месте на графике наблюдается резкое падение величины напора. Величина пьезометрического напора будет меньше полного напора на величину скоростного напора:

.

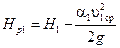(5.8)

Следующее сечение выбирается в конце прямого участка трубы перед или в месте расположения следующего сопротивления. Полный напор в этом сечении будет меньше полного напора в первом сечении на величину потерь напора по длине:

,

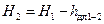(5.9)

где 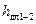– потери по длине между первым и вторым сечениями.

Пьезометрический напор во втором сечении будет меньше полного напора на величину скоростного напора:

.

(5.10)

Для упрощения расчета необходимо помнить, что при равномерном движении жидкости линия пьезометрического напора параллельна линии полного напора. Таким образом, последовательно строятся линии полного и пьезометрического напоров по всей длине трубопровода. Благодаря построенным линиям напоров очень легко установить сечение трубопровода, в котором происходят наибольшие потери напора, что позволяет в случае необходимости предусмотреть мероприятия по их минимизации. На этом же графике в принятом масштабе наносится линия геометрического напора, которая проходит по оси трубопровода.