Ошибка выборки для альтернативного признака
Теорема Бернулли утверждает, что при достаточно большом объеме выборки вероятность Pрасхождения между долей признака в выборочной совокупности р и долей в генеральной совокупности Pг будет стремиться к 1.
 , (4.10)
, (4.10)
Для альтернативного признака среднее квадратическое отклонение равно 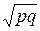 , где
, где 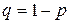 . Тогда средняя ошибки выборки для альтернативного признака равна
. Тогда средняя ошибки выборки для альтернативного признака равна
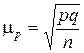 , (4.11)
, (4.11)
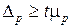 , (4.12)
, (4.12)
Доля в генеральной совокупности Pг неизвестна и может быть только оценена при выборочном наблюдении
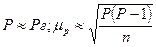 , (4.13)
, (4.13)
При простой случайной выборке средняя квадратическая ошибки определяется по формулам:
| Средняя квадратическая ошибка | Повторная выборка | Бесповторная выборка |
| При определении среднего размера признака | 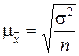 , (4.14) , (4.14)
| 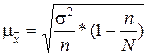 , (4.16) , (4.16)
|
| При определении доли признака | 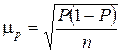 ,(4.15) ,(4.15)
| 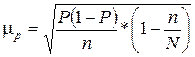 . (4.17) . (4.17)
|
Дата добавления: 2015-08-26; просмотров: 854;
