Класифікація та постановки крайових задач
Розрізняють три основних типи крайових задач для диференціальних рівнянь:
I.Задача Коші: ставиться для рівнянь гіперболічного та параболічного типів шляхом завдання початкових умов, крайові умови відсутні;
II.Крайова задача для рівнянь еліптичного типу: задаються крайові умови, початкові умови відсутні;
III.Змішана задача (початково-крайова задача): ставиться для рівнянь гіперболічного та параболічного типів шляхом завдання як початкових, так і крайові умов.
Для рівняння коливань задача Коші формулюється наступним чином: знайти 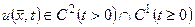 , що задовольняє рівняння
, що задовольняє рівняння
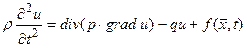 (4.23)
(4.23)
та початкові умови:
 ,
,
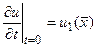 . (4.24)
. (4.24)
Для рівняння дифузії задача Коші формулюється так: знайти 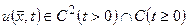 , що задовольняє рівняння
, що задовольняє рівняння
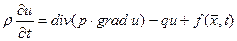 (4.25)
(4.25)
та початкову умову:
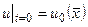 . (4.26)
. (4.26)
Крайова задача для еліптичного рівняння полягає в знаходженні функції 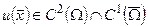 , що задовольняє рівняння
, що задовольняє рівняння
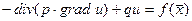 (4.27)
(4.27)
та крайові умові (4.22).
Для рівнянь Лапласа і Пуассона крайова задача з крайові умовою І роду називається задачею Діріхле, з крайові умовою ІІ роду – задачею Неймана. Крайові задачі для рівнянь еліптичного типу можуть бути також зовнішніми та внутрішніми.
Змішана задача для рівнянь гіперболічного типу ставиться так: знайти функцію 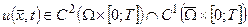 , що задовольняє рівняння коливань (4.23), початкові умови (4.24) та крайову умову (4.22), причому мають виконуватися умови узгодженості:
, що задовольняє рівняння коливань (4.23), початкові умови (4.24) та крайову умову (4.22), причому мають виконуватися умови узгодженості:
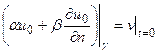 ,
,
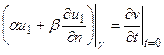 . (4.28)
. (4.28)
І нарешті, змішана задача для рівняння дифузії (4.25) полягає в знаходженні функції 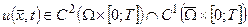 , що задовольняє рівняння (4.25), початкову умови (4.26) та крайову умову (4.22).
, що задовольняє рівняння (4.25), початкову умови (4.26) та крайову умову (4.22).
Дата добавления: 2015-08-26; просмотров: 752;
