Функциональная электроника
Как составляющая средств медицинской электроники. ФЭ – одно из направлений твердотельной электроники, охватывающее использования различных физических явлений в твердых средах для интеграции различных схемотехнических функций в объеме одного твердого тела (функциональная интеграция) и создания электронных устройств с такой интеграцией.
В отличие от схемотехнической интеграции функционально простых элементов (резисторов, конденсаторов, диодов, транзисторов и т. п.), которые локализованы в различных листах твердого тела и способны выполнять сложные схемотехнические функции лишь в совокупности, например, в составе ИС, включающей в себя также элементы связи (межсоединения), при функциональной интеграции сложны схемотехнические функции и по комбинации могут реализоваться физическими процессами, протекающими во всем рабочем объеме твердого тела.
Переход от схемотехнической интеграции к функциональной позволит устранить значительную часть принципиальных и технологических трудностей, связанных с необходимостью формировать в одном кристалле множество структурных элементов и межсоединений.
Схемотехническая интеграция – это технологическая интеграция.
Функциональная интеграция – это физическая интеграция.
Функциональная интеграция – ориентируется на преимущественное использование волновых процессов и распределенного взаимодействия электромагнитных полей с электронами и атомами в твердых телах.
При создании устройств функциональной электроники могут быть использованы различные материалы –полупроводники, магнитодиэлектрики, пьезоэлектрики, сегнетоэлектрики, а также многослойные гомо - и гетероструктуры из этих материалов.
Среди разнообразных приборов функциональной электроники наибольшее распространение получили:
– акустоэлектронные приборы;
– приборы на волнах пространственного заряда в твердом теле;
– приборы с зарядовой связью;
– оптоэлектронные устройства с распределенным взаимодействием и т.п.
Состав элементной базы. Элементную базу СМЭ составляет совокупность различных элементов, участвующих в преобразовании сигналов и информации, которая в них содержится: пассивные дискретные ЭРЭ и простейшие устройства на их основе, например LC-фильтры; активные дискретные элементы – полупроводниковые и электровакуумные приборы (ЭВП); интегральные микросхемы; устройства функциональной электроники и некоторые другие.
Данный курс посвящен рассмотрению элементной базы СМЭ.
Пассивные элетрорадиоэлементы выполняют в СМЭ различные операции над сигналами. Они основаны на таких физических процессах как электрический контакт, взаимодействие электрического тока и магнитного поля, напряжения и электрического заряда и др. К ним можно отнести катушки индуктивности, конденсаторы, резисторы, трансформаторы и т. д.
Элементной базой принято также считать устройства, состоящие из отдельных ЭРЭ, например, LC-фильтры, или из электромеханических элементов (соединители, переключатели, реле).
Полупроводниковые и электровакуумные приборы, являясь активными элементами, по физической сущности функционирования принципиально отличаются от пассивных. Их принцип действия основан на сложных физических процессах, они характеризуются специфическими параметрами, конструкцией и технологией.
В настоящее время дискретные активные элементы обычно используются при больших мощностях, на сверхвысоких частотах и в аппаратуре рентгеновской диагностики.
Интегральные микросхемы – пленочные, гибридные и полупроводниковые разной степени интеграции – наиболее широко применяются в СМЭ. В гибридных ИС используются навесные транзисторы и конденсаторы большой емкости и некоторые другие компоненты, а резисторы, конденсаторы малой емкости, соединения и в редких случаях катушки индуктивности формируются нанесением пленок на поверхности подложки.
Обработка сигналов осуществляется продвижением носителей из области одной статической неоднородности в область другой. При этом происходит непрерывное изменение физических величин – носителей информации, таких как ток, потенциал, концентрация носителей и т.д.
Статические неоднородности характеризуются следующими особенностями: создаются в ходе необратимых технологических процессов в процессе производства; в основном сохраняют характеристики в течение всего срока эксплуатации; жестко связаны с определенными координатами и не могут перемещаться в объеме прибора.
Статические неоднородности являются основой технологической интеграции, т. е. основой создания и функционирования полупроводниковых дискретных приборов и ИС, включая БИС. Направление микроэлектроники, связанное с технологической интеграцией, иногда называют схемотехническим. Этот термин основан на том, что преобразования, которым подвергаются сигналы, определяются как свойствами статических неоднородностей (р-n переходы, образующие транзисторы, диоды и т. п.), так и тем, каким образом они сформированы в ИС и соединяются между собой, т. е. схемой.
Устройства функциональной электроникиприобретают в настоящее время возрастающее значение в элементной базе СМЭ. Функциональная электроника охватывает вопросы получения комбинированных средств с наперед заданными свойствами и создание различных электронных устройств методами физической интеграции, т. е. использование таких физических принципов и явлений, реализация которых позволяет получить компоненты со сложным функциональным назначением в отличие от технологической интеграции, предусматривающей конструирование интегральных микросхем на основе функционально простых элементов типа транзисторов, диодов, резисторов и т. д.
В функциональной электронике (ФЭ) использованы новые физические принципы и эффекты, характерной особенностью которых является наличие и использование для обработки и хранении информации динамических неоднородностей в однородном объеме твердого тела. Примером таких динамических неоднородностей могут быть цилиндрические магнитные домены, пакеты зарядов в приборах с зарядовой связью, волны деформации кристаллической решетки в приборах на поверхностных акустических волнах и т. д.
Динамические неоднородности создаются физическими методами. Их появление, перемещение и исчезновение в объеме твердого тела не связано с процессом изготовления устройства. Особенностями динамических неоднородностей является то, что они создаются физическими средствами в ходе эксплуатации прибора, а не технологическими в процессе производства; могут возникать и исчезать, а также изменять свои характеристики во времени; могут существовать длительное время, и эта длительность определяется функциональными задачами устройства; не связаны жестко с координатами; являются непосредственными носителями информации, которая может быть представлена как в цифровой, так и в аналоговой форме.
.
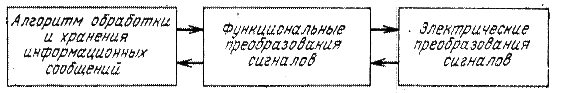
Классификация функциональных преобразований. Информационная радиоэлектронная система создается с целью обработки, хранения и передачи определенных информационных сообщений. Такие сообщения формируются с помощью физического носителя сигнала, отражающего возмущение соответствующей материальной среды. Наиболее распространенным физическим носителем является электрический ток, оптические, акустические и магнитные явления, которые, как правило, в последствии преобразуются в электрический ток. В итоге в работающей ИС протекают два взаимосвязанных процесса: электрическое преобразование сигналов и обработка информационных сообщений (рис. 1.2).
Рис. 1.2. Взаимосвязь информационных, функциональных и электрических преобразований сигналов.
В подавляющем большинстве случаев оба вышеуказанных процесса связаны между собой сложными зависимостями, которые не всегда можно выразить в явной форме. Для того, чтобы реализовать даже простые алгоритмы обработки информационных сообщений, необходимо предусмотреть в проектируемой ИС десятки, а иногда и сотни преобразований электрического сигнала.
Для упрощения проектирования, процессы обработки информационных сообщений и электрических преобразований сигналов чаще всего связывают через третий (буферный) процесс — функциональное преобразование сигналов. Под функциональным преобразованием будем понимать отображение (переход) одного состояния или кодовой комбинации сигналов в другое состояние или кодовую комбинацию.
Информационные сообщения могут быть сформированы с помощью как аналогового, так и дискретного преобразования (кодирования). При дискретном кодировании одно слово сообщения формируется путем составления определенных комбинаций из многих сигналов,

Рис. 1.3. Классификация функциональных преобразований сигнала.
которые имеют ограниченное число состояний*, а их параметры изменяются, как правило, скачкообразно. В связи с таким разделением способов формирования сообщений появилось три вида преобразователей: аналоговые, дискретные (цифровые) и смешанные (рис. 1.З).
При смешанных преобразованиях состояние входных сигналов может изменяться непрерывно (как во времени, так и по уровню), а состояние выходных сигналов — дискретно и наоборот. Возможно совместное преобразование аналоговых и дискретных сигналов. С помощью известной теоремы В.А. Котельникова аналоговые сигналы можно преобразовывать в смешанные или полностью дискретные, почти не искажая их информационного содержания [1.38].
Функциональные преобразования могут быть детерминированными или вероятностными. В первом случае каждому состоянию или кодовой комбинации входных сигналов однозначно соответствует только одно состояние или одна кодовая комбинация выходных сигналов из множества возможных. Во втором случае соответствие между состояниями и кодовыми комбинациями входных и выходных сигналов задается вероятностными законами.
__________
Чаще всего используются два состояния: «нуль» и «единица».
Дискретные функциональные преобразования разделяются на два больших класса: импульсные и логические; первые широко применяются в радиосвязи, радиолокации, радионавигации, телевидении и т. п.; вторые используются в устройствах кодирования и декодирования в радиотехнических системах, цифровой телеметрии, вычислительной технике и автоматических устройствах управления. Аргументы логических функций и сами функции принимают только два значения: «нуль».или «единица» (0 или 1). Эти преобразования или, как их еще называют, логические операции подчиняются законам математической логики. В табл. 1.1 показано различие аналоговых, импульсных и логических преобразований.
Таблица 1.1
| Характеристики преобразования | Виды преобразования | ||||
| Аналоговые | импульсные | логические | |||
| варианты преобразований | |||||
| Число состояний сигналов по шкале времени | ∞ | ∞ | nt | nt | |
| Число состояний сигналов по шкале уровней | ∞ | ny | ∞ | ny | |
| Число сигналов, формирующих одно слово сообщения | p1 | p2 | p3 | l | |
| Число возможных комбинаций сигналов, формирующих одно слово сообщения | — | m |
Примечание. Здесь m — число дискретных сигналов (объем алфавита): nt и ny — число квантованных изменений параметров сигналов по времени и по уровню.
Для того чтобы как-то систематизировать множество аналоговых, цифровых и смешанных функциональных преобразований, выделим в каждом из них три подкласса: генерирование сигналов, усиление и трансформация сигналов, формирование сигналов.
Первый и второй подклассы пояснений не требуют. В третий подкласс сведены все преобразования, связанные с изменением формы и Спектрального состава сигналов. Это наиболее обширный подкласс, включающий модуляцию и детектирование сигналов, смешение, фильтрацию, ограничение и т. д. Форма и спектральный состав сигналов связаны между собой известными преобразованиями Фурье [1.38]. Следовательно, можно взять за основу изменение формы сигналов (временной подход) или изменение спектрального состава (спектральный подход). При дальнейшей классификации подкласса формирования сигналов, приведенной на рис. 1.3, выбран спектральный подход. Используя теоремы о спектрах, можно выделить в этом подклассе, по крайней мере, шесть видов математических преобразований, указанных в табл. 1.2.
Таблица 1.1
| Название теорем о спектрах | Математическая формулировка теорем | Примеры технического использования |
| Теорема о спектре производной сигнала | 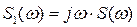
| Дифференцирование сигналов |
| Теорема о спектре интегрирования сигнала | 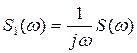
| Интегрирование сигналов |
Теорема о смещении сигнала по шкале времени 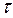
| 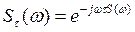
| Задержка сигналов |
| Теорема о сумме спектров | 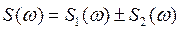
| Смещение и фильтрация сигналов |
| Теорема о спектре произведения (свёртка функций) | 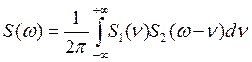
| Умножение на весовую функцию |
| Теорема подобия спектров | 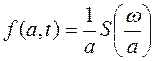
| Временное сжатие сигналов |
Каждая микросхема, решающая ту или иную функциональную задачу, состоит из ряда элементарных функциональных преобразователей (ЭФП). Сложность каждого преобразователя зависит от сложности синтезируемой микросхемы, её конкретных свойств и квалификации проектировщика. Конечным продуктов функционального синтеза все чаще становится мелкомасштабная часть микросхемы.
Все ЭФП можно условно разбить на две категории: электрические ЭФП, с помощью которых в процессе функционального синтеза ИС можно моделировать преобразования электрических сигналов, и так называемые специальные ЭФП, отражающие функциональные механизмы преобразования неэлектрических величин в электрические сигналы и дополняющие связь ИС с аппаратурой и внешней средой. Специальные ЭФП можно разбить на четыре класса: механические (ЭФП перемещения, ускорения, веса, объема и т. п.), физические (ЭФП магнитные, оптические, тепловые и т. п.), химические (ЭФП концентрации и т. п.) и биологические (ЭФП биопотенциальные, фоторецепторные, метаболические).
Классификация электрических ЭФП в основном совпадает с классификацией, приведенной на рис. 1.1. Электрические ЭФП можно разделить на четыре класса: аналоговые (АЭФП), импульсные (ИЭФП), смешанные (СЭФП) и логические (ЛЭФП). Первые два класса в свою очередь разбиваются на подклассы: ЭФП генерирования сигналов, ЭФП усиления и трансформации сигналов и ЭФП формирования сигналов. Последний обширный подкласс ЭФП удобно подразделить еще на две группы: ЭФП индивидуального формирования сигнала (ограничение, умножение и деление частоты, дифференцирование и интегрирование, задержка во времени т. п.) и ЭФП группового формирования сигналов (модуляция и детектирование, смешение и фильтрация, различение сигналов и т. п.). Смешанные ЭФП подразделяются на два подкласса: ЭФП видеосигналов и ЭФП радиосигналов. Логические ЭФП подразделяются на ЛЭФП с запоминанием (управляемые и неуправляемые) и ЛЭФП без запоминания (статические и динамические).
Каждый ЭФП характеризуется своим символом и определяющими его параметрами*. В качестве символа ЭФП мы выбрали прямоугольник со значком или буквами в середине (отражающими назначение преобразования или форму выходного сигнала) и внешними стрелками, характеризующими число входов и выходов. Параметры ЭФП удобно проставлять по внешнему периметру символа. Число параметров зависит от типа ЭФП и точности преобразования, задаваемой Проектировщиком (мы проставим только наиболее характерные из них). В табл. 1.3 приводится далеко не полный перечень преобразований, используемых в аналоговых, импульсных, смешанных и логических ЭФП [1.4].
Таблица 1.3
| Принципиальная схема | Тип преобразования |
| Аналоговые ЭФП | |
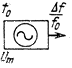
| Генерирование синусоидального сигнала:  — частота автоколебаний; — частота автоколебаний; 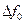 — нестабильность частоты; — нестабильность частоты; 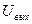 — амплитуда выходного напряжения — амплитуда выходного напряжения
|

| Усиление: 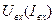 — амплитуда входного напряжения (тока); — амплитуда входного напряжения (тока); 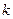 — коэффициент усиления по напряжению (току), — коэффициент усиления по напряжению (току), 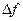 — полоса пропускания — полоса пропускания
|
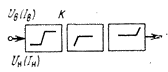
| Двустороннее ограничение напряжения (тока): 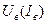 и — соответственно верхний и нижний пороги ограничения; и — соответственно верхний и нижний пороги ограничения; 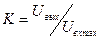 — коэффициент изменения величины сигнала после ограничения — коэффициент изменения величины сигнала после ограничения
|

| Умножение частоты: 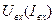 — амплитуда входного сигнала; — амплитуда входного сигнала; 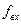 — частота входного сигнала; — частота входного сигнала; 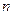 — коэффициент умножения частоты; — коэффициент умножения частоты; 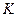 — коэффициент изменения амплитуды (мощности) сигнала — коэффициент изменения амплитуды (мощности) сигнала
|
_____________
*Функциональные элементы класса ЛЭФП обычно характеризуются только символом.
Продолжение табл. 1.3
| Принципиальная схема | Тип преобразования |

| Деление частоты: 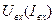 — амплитуда входного сигнала; — амплитуда входного сигнала; 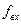 — частота входного сигнала; — частота входного сигнала; 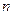 — коэффициент деления частоты — коэффициент деления частоты
|

| Фильтрация: 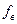 — верхняя частота среза; — верхняя частота среза; 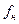 — нижняя частота среза; — нижняя частота среза; 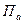 — коэффициент прямоугольности на уровне — коэффициент прямоугольности на уровне 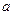 ; ; 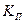 — коэффициент передачи — коэффициент передачи
|
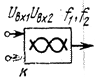
| Смешение: 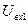 — амплитуда первого входного сигнала; — амплитуда первого входного сигнала; 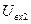 — амплитуда второго входного сигнала; — амплитуда второго входного сигнала; 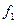 и и 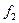 — частоты первого и второго сигналов; — частоты первого и второго сигналов; 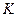 — коэффициент пропорциональности между входными сигналами — коэффициент пропорциональности между входными сигналами
|
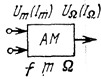
| Амплитудная модуляция: 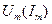 — амплитуда несущего сигнала; — амплитуда несущего сигнала; 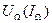 — амплитуда модулирующего сигнала; — амплитуда модулирующего сигнала; 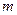 — коэффициент, характеризующий глубину модуляции; — коэффициент, характеризующий глубину модуляции; 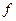 — частота несущего сигнала; — частота несущего сигнала; 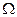 — частота модулирующего сигнала — частота модулирующего сигнала
|
| Импульсные ЭФП | |
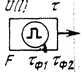
| Генерирование прямоугольных импульсов: 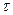 — длительность импульса; — длительность импульса; 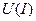 — величина импульсного напряжения (тока); — величина импульсного напряжения (тока); 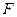 — частота повторения импульсов; — частота повторения импульсов; 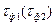 — длительность переднего фронта импульса — длительность переднего фронта импульса
|

| Генерирование линейно изменяющего (пилообразного) сигнала: 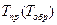 — время прямого (обратного) хода сигнала; — время прямого (обратного) хода сигнала; 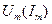 — максимальная величина сигнала; — максимальная величина сигнала; 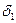 и и 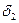 — коэффициенты нестабильности амплитуды и скорости нарастания сигнала; — коэффициенты нестабильности амплитуды и скорости нарастания сигнала; 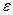 — коэффициент нелинейности прямого хода сигнала — коэффициент нелинейности прямого хода сигнала
|
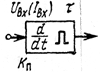
| Дифференцирование прямоугольного импульса: 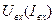 — напряжение (ток) входного импульса; — напряжение (ток) входного импульса; 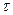 — длительность выходных импульсов (на уровне 0.5); — длительность выходных импульсов (на уровне 0.5); 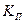 — коэффициент передачи — коэффициент передачи
|

| Интегрирование прямоугольного импульса: 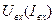 — напряжение (ток) входного импульса; — напряжение (ток) входного импульса; 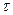 — длительность выходного импульса (на уровне 0.5) — длительность выходного импульса (на уровне 0.5)
|

| Разделение импульсов по амплитуде: 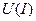 — напряжение (ток) выделяемых импульсов; — напряжение (ток) выделяемых импульсов; 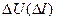 — допустимый разброс селекции — допустимый разброс селекции
|
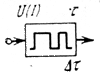
| Разделение импульсов по длительности: 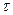 — длительность выделяемых импульсов; — длительность выделяемых импульсов; 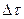 — допустимый разброс — допустимый разброс
|
Окончание табл. 1.3
| Смешанные ЭФП | |

| Различение амплитуды ( 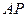 ): ): 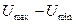 — диапазон изменения величины аналогового сигнала; — диапазон изменения величины аналогового сигнала; 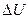 — допустимый разброс чувствительности амплитудного различения — допустимый разброс чувствительности амплитудного различения
|

| Амплитудное детектирование радиоимпульсов: 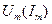 — амплитуда несущего сигнала; — амплитуда несущего сигнала; 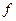 — частота несущего сигнала; — частота несущего сигнала; 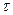 — длительность радиоимпульсов; — длительность радиоимпульсов; 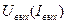 — величина выходного сигнала после детектирования — величина выходного сигнала после детектирования
|
| Логические ЭФП | |

| Сложение сигналов (дизъюнкция). Символически записывается 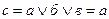 или или 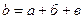 (сигнал на выходе существует, если на входы подан хотя бы один сигнал) (сигнал на выходе существует, если на входы подан хотя бы один сигнал)
|

| Умножение сигналов (конъюнкция). Символически записывается 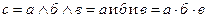 (сигнал на выходе существует, если на все входы поданы сигналы) (сигнал на выходе существует, если на все входы поданы сигналы)
|

| Отрицание сигнала (инверсия). Символически записывается 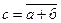 ; ; 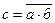
|
Число типов аналоговых, импульсных и смешанных ЭФП весьма велико. В отличие от указанных типов ЭФП полная система переключательных ЛЭФП (функции с двумя состояниями) разработана еще Дж. Булем в прошлом веке. Таких ЛЭПФ всего 16. Помимо приведенных и табл. 1.3, существуют еще ЛЭФП эквивалентности или равнозначности 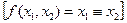 , импликации
, импликации  в
в 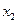
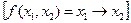 , Шеффера
, Шеффера 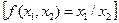 , Вебба
, Вебба 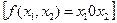 , сложения по модулю 2
, сложения по модулю 2 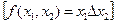 и другие. Принцип действия перечисленных ЛЭФП показан в табл. 1.4.
и другие. Принцип действия перечисленных ЛЭФП показан в табл. 1.4.
Таблица 1.4

| 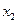
| Разновидности ЛЭФП | ||||
| ЛЭФП эквивалентности | ЛЭФП импликации | ЛЭФП Шеффера | ЛЭФП Вебба | ЛЭФП сложения по модулю 2 | ||
Практически наиболее часто используют ЛЭФП сложения (ИЛИ), умножения (И) и отрицания (НЕ). ЛЭФП достаточно хорошо рассмотрены в работах [1.35-1.41] и др.
Основной задачей функционального синтеза ИС является построение ее мелкомасштабной схемы, обладающей высокой степенью однородности. Под мелкомасштабной функциональной схемой (моделью) ИС будем понимать документ, определяющий число ЭФП, комплекс которых полностью отражает характер и последовательность происходящих в ИС функциональных преобразований сигналов, их типы и взаимосвязь между ними. Процесс синтеза функциональной схемы, в основном; сводится к ее последовательной детализации с помощью разукрупнения функциональных элементов вплоть до ЭФП. Первый этап указанного синтеза, предусматривающий разделение общего алгоритма функционирования ИС на ряд частных и менее сложных алгоритмов, осуществляется посредством специальной отработки технического задания.
Частные алгоритмы решения основных и вспомогательных задач взбираются по степени их важности. Первая, основная задача реализуется в виде определенного участка синтезируемой схемы, она становится как бы центром (ядром) ее «кристаллизации». Этот участок последовательно наращивается по мере реализации основных, а затем и вспомогательных задач алгоритма. Полученная таким образом схема может быть относительно крупномасштабной. Поэтому ее детализируют последовательным понижением уровня сложности функциональных элементов, т. е. с помощью «расщепления» их на простые. В результате общее число элементов интегральной микросхемы увеличивается.
При синтезе относительно несложных функциональных схем последние непосредственно составляются из ЭФП. При синтезе логических схем со множеством входов и одним выходом придерживаются следующих правил: а) выбирается так называемый базис или система ЛЭФП (чаще всего схемы И, ИЛИ, НЕ), из которых будет синтезироваться интегральная схема; б) алгоритм работы схемы описывается известными законами математической логики через соотношения, определяемые выбранными ЛЭФП; в) общее выражение алгоритма разбивают на ряд менее сложных взаимосвязанных между собой частных функций; г) на основе выбранной системы частных функций строят логическую схему.
Для иллюстрации рассмотрим два примера.
Пример 1.1. Синтезировать логическую функциональную схему автоматического устройства.
Входы. Схема имеет четыре входа, на которые подаются потенциальные сигналы (логические «нуль» и «единица»).
Выходы. Схема имеет один сигнальный выход.
Алгоритм работы схемы имеет вид 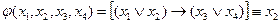

Рис. 1.4. Логическая функциональная схема с компонентами уровня 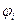 (а) и уровня ЛЭФП (б).
(а) и уровня ЛЭФП (б).
В качестве базиса выберем схемы: И, ИЛИ, НЕ. Выразим алгоритм через эти три типа ЛЭФП (избавимся от ЛЭФП импликации и эквивалентности):

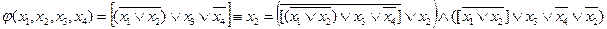 .
.
Разобьем полученное выражение на более простые функции:
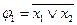 ;
; 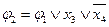 ;
; 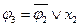 ;
; 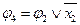 ;
; 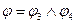 .
.
На рис. 1.4 приведены варианты логической схемы с компонентами уровня 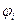 и мелкомасштабной микросхемы с элементами уровня ЛЭФП.
и мелкомасштабной микросхемы с элементами уровня ЛЭФП.
Пример 1.2. Синтезировать аналоговую функциональную схему распределителя сигналов.
Входы. Схема имеет один сигнальный вход. На него подается высокочастотный ЧИМ/АМ сигнал, представляющий серию импульсных посылок. Частоты: несущего сигнала 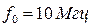 , заполнения импульсов
, заполнения импульсов 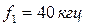 ;
; 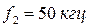 ;
; 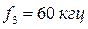 . Длительность импульсов —
. Длительность импульсов — 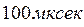 . Величина входного сигнала
. Величина входного сигнала 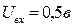 .
.
Выходы. Схема имеет три выхода. С каждого из них снимаются видеоимпульсы, соответствующие частотам заполнения: выход 1 — 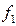 ; выход 2 —
; выход 2 — 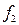 и выход 3 —
и выход 3 — 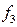 . Амплитуды выходных сигналов должны быть равны 1 в.
. Амплитуды выходных сигналов должны быть равны 1 в.


Алгоритм работы схемы. Первая основная задача алгоритма: выделить из высокочастотного ЧИМ/АМ сигнала импульсы посылки и разделить их по трем каналам. Вторая основная задача: обеспечить заданные параметры выходных сигналов. Реализация первой основной задачи приведена на рис. 1.5, а. Полная функциональная схема распределителя сигналов приведена на рис. 1.5, б. В схеме используется десять АЭФП трех типов: ограничения, фильтрации и усиления.
Рис. 1.5. Реализация первой основной задачи (а) и полная аналоговая функциональная схема распределителя сигналов (б):
Для 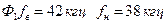 ; для
; для 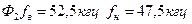 ; для
; для 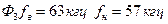 ;
; 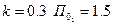 .
.
После определения состава ЗФП следует этап электрического моделирования, основной задачей которого является синтез и оптимизация алгоритма процессов преобразования электрических сигналов создаваемой ИС. Указанный алгоритм, как известно, неразрывно связан со структурой электрической модели ИС, синтезируемой одновременно с его разработкой. Модель обычно представляется в виде электрической Цепи или схемы, состоящей из схемных элементов. При электрическом моделировании радиотехнических устройств, включая ИС, используют два основных вида схем-моделей: принципиальные электрические схемы и эквивалентные электрические схемы. Последние отличаются предельной мелкомасштабностью. Число типов элементов эквивалентной схемы стремятся строго ограничивать. Число типов элементов принципиальной схемы практически не ограничено. К ним относятся: резисторы, конденсаторы, индуктивные элементы, трансформаторы, диоды, транзисторы, тиристоры, кварцевые резонаторы, RC-структуры, элементы памяти и т. д., а также специально изготавливаемые отдельные элементы и участки ИС*.
_____________
*Этот перечень с каждым годом увеличивается по мере разработки и выпуска промышленностью новых типов элементов и приборов.
На практике элементы принципиальной схемы являются дискретными и неидеальными. Они характеризуются паразитными параметрами, зависящими от конструкции, частоты и уровня сигнала Сложность электрических преобразований, выполняемых этими компонентами, колеблется в широких пределах. Каждый из элементов с известной степенью приближения можно отразить своей эквивалентной схемой-моделью
Тема 1.4 Интегральные микросхемы, как одна из составляющих частей РЭА

Электрическое моделирование ИС может быть как расчетно-теоретическим, так и натурным (экспериментальным) [1.17] (последнее обычно дополняет первое). Расчетно-теоретическое моделирование в свою очередь подразделяется на аналитическое и машинное. В основе аналитического моделирования лежат известные аналитические преобразования, используемые в теории цепей [1.42—1.44]. При машинном моделировании на ЦВМ используются арифметические операции сравнения, перебора [1.19, 1.25, 1.26]. При расчетно-теоретическом моделировании в качестве исследуемого объекта применяются как принципиальная, так и эквивалентная схемы. При натурном моделировании используется только принципиальная схема.
Рис. 1.6. Классификация типов электрических моделей и моделирования ИС
Основным методом этого моделирования является метод граничных испытаний схемы [1.22, 1.45]. Классификация типов электрических моделей приведена на рис. 1.6.
В заключение остановимся на классификации используемых на практике элементов принципиальных электрических схем, приведенной на рис. 1.7. Эти элементы прежде всего характеризуются числом полюсов (входов и выходов электрического тока). Существуют двухполюсные (резисторы, конденсаторы, диоды), трехполюсные (транзисторы, RC-структуры), четырёхполюсные (трансформаторы, тиристоры) и в общем случае n-полюсные элементы. С ростом числа полюсов конструктивная сложность элемента и его возможности преобразования сигнала, как правило, существенно возрастают; одновременно увеличивается гибкость управления режимом работы. Элементы делятся на пассивные и активные. Пассивные элементы, обладающие положительным сопротивлением ( 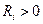 ), расходуют мощность полезного сигнала, чаще всего рассеивая ее в виде тепловых потерь. Активные элементы усиливают мощность полезного сигнала, преобразуя энергию источников питания в энергию полезного сигнала. Знак и величина угла
), расходуют мощность полезного сигнала, чаще всего рассеивая ее в виде тепловых потерь. Активные элементы усиливают мощность полезного сигнала, преобразуя энергию источников питания в энергию полезного сигнала. Знак и величина угла 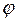 сдвига фаз между током и напряжением сигнала на каждом полюсе элемента определяют его импеданс. В общем случае он будет комплексным. При
сдвига фаз между током и напряжением сигнала на каждом полюсе элемента определяют его импеданс. В общем случае он будет комплексным. При 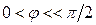 импеданс будет носить индуктивный, при
импеданс будет носить индуктивный, при 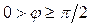 — емкостной, а при
— емкостной, а при  — омический характер. При
— омический характер. При 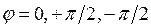 двухполюсники вырождаются в резисторные, индуктивные и емкостные элементы соответственно.
двухполюсники вырождаются в резисторные, индуктивные и емкостные элементы соответственно.

Зависимость тока сигнала от его напряжения на каждом полюсе элемента может быть как линейной, так и нелинейной. Нелинейными зависимостями обычно обладают активные элементы. Наиболее часто встречаются нелинейности N- и S-вида.
Рис. 1.7. Классификация преобразовательных схемных элементов (компонентов) ИС.
По режиму работы элементы можно подразделить на аналоговые и ключевые (спусковые). Первые характеризуются сравнительно плавным изменением параметров во времени, вторые — скачкообразным (в идеале — мгновенным). Закономерности изменения параметров аналоговых элементов, во многом определяющие форму и спектральный состав сигнала, существенно влияют на информационную часть последнего. Изменения параметров ключевых элементов, как правило, не влияют на формирование информационной части сигнала, которая определяется правилами кодирования
Последний признак рассматриваемой классификации характеризует степень пространственного распределения параметров элемента. С этой точки зрения элементы подразделяются на элементы с сосредоточенными параметрами и элементы с распределеннымипараметрами.
Основной задачей электрического моделирования ИС является оптимальный синтез ее принципиальной электрической схемы (модели). Для конструктора эта схема содержит информацию: о числе схемных элементов в ИС и их электрической взаимосвязи друг с другом; о типах этих элементов и их основных электрических параметрах и характеристиках; о допусках на эти параметры и характеристики. Процесс разработки принципиальной схемы, как и любой другой модели ИС, подразделяется на три этапа: структурный синтез схемы, анализ ее параметров и принятие решения о пригодности модели. На этапе структурного синтеза определяется электрическая схема, тип входящих в нее элементов, номинальные значения их параметров. Рассмотрим эту операцию более подробно. Прежде всего отметим, что синтез электрических схем (моделей) ИС отличается от синтеза электрических схем обычных узлов РЭА следующими особенностями:
1. Не все классические дискретные схемные элементы технически можно или экономически выгодно выполнять в виде ИС. К таким элементам относятся трансформаторы токов и напряжений, индуктивности, большие емкости, настроечные элементы.
2. Не все элементы, сформированные в ИС, имеют аналоги среди дискретных элементов, выпускаемых промышленностью. Так, например, нет дискретного аналога интегральной RC-структуры. Однако, если даже такие аналоги и имеются, то электрические характеристики и параметры интегральных и дискретных элементов обычно отличаются друг от друга. Так, например, интегральный диффузионный резистор, в отличие от дискретного резистора типа МЛТ, имеет большую паразитную распределенную емкость.
3. Электрические связи между элементами в ИС существенно «дополнены» паразитными связями через общую для них подложку. Поэтому принципиальная электрическая схема воспроизводит только важнейшие процессы и характеристики ИС, и то с определенной степенью приближения.
Этап структурного синтеза электрических принципиальных схем проектируемых PIC является сложным и ответственным процессом. Этот этап выполняется наиболее квалифицированными схемотехниками. В своей работе они используют информацию о ранее выполненных разработках подобного рода, технические условия, технологические ограничения со стороны планируемого завода-изготовителя, личный опыт и инженерную интуицию. Структура электрической схемы ИС во многом определяется характером выполняемых ею преобразований сигналов. Аналоговое и импульсные схемы выполняют, как правило, точные электрические преобразования, в силу чего их характеристики чувствительны к вариации параметров элементов, к реакции на паразитную обратную связь и флюктуациям параметров входного сигнала. При проектировании и изготовлении этих схем требуется большая точность.
Логические ИС. Дискретные логические схемы характеризуются быстродействием (величиной задержки распространения сигнала), нагрузочной способностью (коэффициентом разветвления выходных каналов), потребляемой мощностью. Эти схемы могут быть выполнены как на ЭРЭ биполярных и полевых транзисторах, так и на УФЭ магнитных, оптоэлектронных, криогенных и других устройствах. Схемы на биполярных транзисторах подразделяются на следующие типы: диодно-транзисторные логические (ДТЛ), транзисторно-транзисторные логические (ТТЛ), транзисторные логические с непосредственными (или резистивными, или резистивно-емкостными) связями (ТЛНС), логические схемы переключения тока (ЛСПТ), триггеры. Примеры указанных типов схем приведены соответственно на рис. 1.8 – 1.12. Эти схемы (за исключением триггера) выполняют логическую операцию (преобразование) И–HE/ИЛИ–НЕ. Их основные параметры сведены в табл. 1.5.
Таблица 1.5
| Параметры схем | Типы схем | |||||
| ДТЛ | ТТЛ | ТЛНС | ЛСМТ | Триггер | ||
| Задержка распространения сигнала, нсек | 8...50 | 6...45 | 10...200 | 5...6 | 40...250 | |
| Потребляемая мощность, мВт | 7,5...30 | 12...15 | 3...27 | 35...70 | 2...90 | |
| Нагрузочная способность (коэффициент разветвления по выходу) | 4...20 | 7...20 | 4...16 | 20...25 | 10...12 | |
| Помехоустой-чивость, в | 0,5…1 | 0,5…1 | 0,15…0,35 | 0,25…0,4 | 0,1…1,0 | |
| Рабочий диапазон температур, °С | -60...+125 | -60...125 | -60...+125 | 0...+70 | 0...+65 -60...+125 |
Широкое распространение получили также логические схемы на МДП (МОП)-транзисторах [1.52]. На рис. 1.13 и 1.14 приведены схемы совпадений типа НЕ—И и триггера. Двухвходовые схемы совпадений (НЕ—И) с параллельным и последовательным соединением МОП-транзисторов работают следующим образом. В схеме с параллельным соединением (рис. 1.1.3, а) транзисторы в исходном состоянии открыты, а в схеме с последовательным соединением (рис. 1.13,6) — закрыты. Только одновременная подача входных сигналов на затворы приборов приводит к срабатыванию схемы. Наряду с операцией II схема инвертирует сигнал. Задержка распространения сигнала в схеме примерно 170—400 нсек. Быстродействие схемы с параллельным включением транзисторов выше. Потребляемая мощность порядка 4...15 мВт. Непосредственные связи в схеме триггера обеспечивают максимальное быстродействие (задержка распространения сигнала 10...80 нсек). Потребляемая мощность схемы 5...20 мВт.
Аналоговые и импульсные ИС. Эти схемы стали разрабатываться промышленностью в 1964 г. В настоящее время разработаны серии усилителей, генераторов, модуляторов, фильтров, стабилизаторов напряжения и т. п. В настоящее время существует тенденция построить унифицированную серию ИС по каждому основному типу преобразования сигнала (типу функции). Успехи в этом направлении пока ощутимы в области линейных усилителей, хотя имеется множество попыток разработать ИС, реализующие другие функции. Среди класса усилителей хорошо освоены в интегральном исполнении так называемые операционные (решающие) усилители (ОУ), позволяющие выполнять в ЭВМ операции сложения, вычитания, интегрирования, дифференцирования, изменения знака и т. д., а при использовании ОУ в аналоговых или импульсных устройствах — функции усиления, сравнения, детектирования и фильтрации.
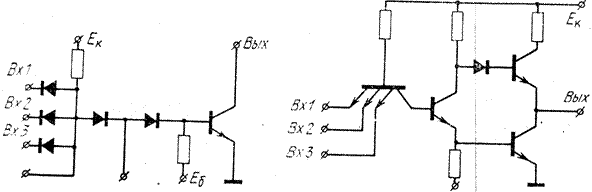
Рис. 1.8. ДТЛ-схема. Рис. 1.9. ТТЛ-схема.

Рис. 1.10. ТЛНС-схема с непосредственными связями
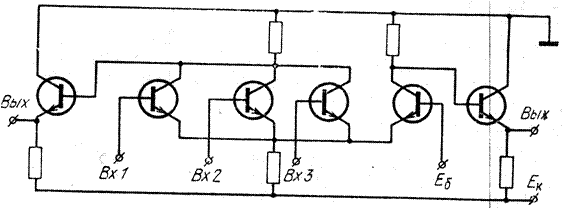
Рис. 1.11. ЛСПТ-схема.
 |
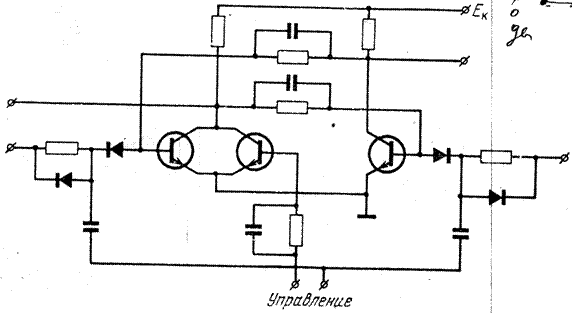
Рис. 1.12. Схема триггера на биполярных транзисторах.
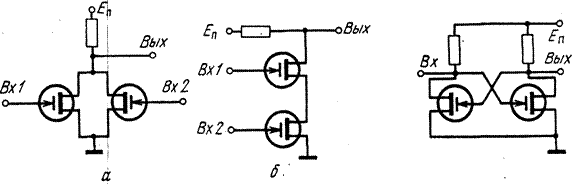
Рис. 1.13. Рис. 1.14.
Рис. 1.13. Двухвходовая схема совпадения НЕ — И с параллельным (а) и последовательным соединением МДП-транзисторов (б).
Рис. 1.14. Схема триггера с непосредственными связями на МДП-транзистора.х.
Электрическая принципиальная схема одного из типовых операционных усилителей приведена на рис. 1.15 [1.54]. Она содержит входной и выходной каскады, а также каскад обратной связи; схема собрала на 4 транзисторах p—n—p и n—p—n-типа и 15 резисторах. Как и дифференциальный усилитель, операционный усилитель имеет два высокоомных симметричных входа, на которые подается разность напряжений сигналов, и низкоомный несимметричный выход. ОУ обладает высоким коэффициентом усиления по току и сильной отрицательной обратной связью. Сигнал по первому входу инвертируется на выходе, а по второму входу не инвертируется. В целях исключения самовозбуждения на высоких частотах к клеммам 4,5 и 6 подключаются внешние развязывающие RC-фильтры Диапазон рабочих температур усилителя —55°...+125°С. Коэффициент усиления 100, входное предельное напряжение Uвх ≈ 5 мв, входное сопротивление Rвх = 900 ком, температурный дрейф нуля примерно 10 мкв/°C
Из точных аналоговых преобразований сигнала, которые можно выполнять с помощью операционного усилителя, в настоящее время достаточно хорошо осуществляется фильтрация сигнала [1.52, 1.53]. Структурная схема так называемых активных фильтров приведена на рис. 1.16. Она содержит частотно-избирательные элементы в цепи обратной связи операционного усилителя и перед каждым из его входов. В качестве этих элементов можно использовать емкости и индуктивности, но лучше всего применять RC-структуры. Путем подбора параметров этих структур можно реализовать почти любую функцию передачи, т. е. построить фильтр практически с любой характеристикой.
Рис 1.15. Электрическая принципиальная схема операционного усилителя в интегральном исполнении:
 |
1 — инвертирующий вход; 2 — неинвертирующий вход; 3— выход; 4, 5, б — выводы подключения внешних цепей.
 Рис. 1.16 Структурная схема активного фильтра, построенного на основе операционного усилителя
Рис. 1.16 Структурная схема активного фильтра, построенного на основе операционного усилителя
|
ИС с перестраиваемой структурой. Разработка каждой новой ИС сопряжена со значительными затратами. В силу известных трудностей унификации аналоговых и импульсных ИС все же велико. Поэтому в настоящее время разрабатываются схемы с перестраиваемой структурой. Перестройку можно осуществлять двумя методами: с помощью формирования недостающих соединений печатного монтажа ИС и с помощью электрического управления.
Сущность первого метода проиллюстрируем на примере логических монолитных ИС марки ХС-157, выпускаемой фирмой «Моторола» [1.55].
В кремниевой подложке сформированы 12 одинаковых ДТЛ, принципиальная схема которых приведена на рис. 1.17. ДТЛ-схема выполняет операцию НЕ-ИЛИ. В каждой ДТЛ-схеме отсутствуют соединения диодов с выходными нагрузочными резисторами. Все 12 схем электрически изолированы друг от друга. Все межэлементные соединения, указанные на рис. 1.17, выполняются фирмой-изготовителем ИС. Они формируются в виде однослойного печатного монтажа. Сверху наносится изоляционная маска из стекла или SiO2 таким образом, чтобы через ее «окна» были открыты контактные площадки ДТЛ-схем. Второй слой межэлементных соединений проектирует и наносит фирма-потребитель ИС.
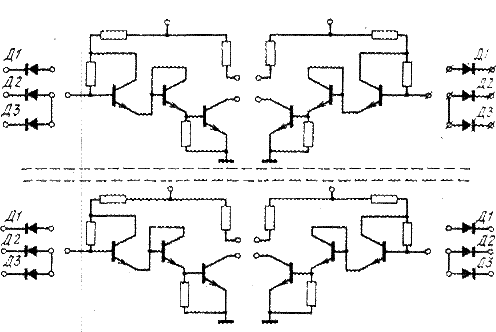 |
Сущность второго метода сводится к переключению отдельных участков схемы с помощью электронных ключей. Внешние выводы
Рис. 1.17. Не полностью «собранная» логическая схема.
ключей всегда находится под управляющим потенциалом. Этот метод еще не доведен до промышленного применения. Проиллюстрируем его на примере схемы детектора уровня, изображенной на рис. 1.18, [1.56].
В схеме предусмотрены четыре p—n—p—n-переключателя, подключающих или отключающих Основные элементы и участки схемы. Сигналы на управляющие электроды переключателей подаются от внешних цепей. При включении только переключателя Кл1 схема работает следующим образом. Положительный входной сигнал вместе с опорным напряжением, снимаемым с делителя П1, подается на затвор полевого транзистора 77. При достижении потенциала насыщения полевой транзистор открывается и включает в работу обычный биполярный транзистор Т2, который в свою очередь открывает диод Д1. В результате на вход схемы через цепь о. с. подается небольшой по величине синфазный сигнал. Величину этого сигнала (коэффициент обратной связи) и запаздывание схемы можно регулировать, изменяя сопротивление цепи обратной связи, в частности R2. Выбирая это сопротивление достаточно большим, мы устанавливаем режим работы детектора уровня. Транзистор ТЗ согласует схему с нагрузкой. При включении только переключателя КлЗ (вместо цепочки R2, R3, Д1 включается R1) схема работает как бистабильный мультивибратор, запускаемый знакопеременной последовательностью импульсов. При включении только переключателя Кл2 (вместо R1 включается С1) и подаче на вход стробирующих сигналов схема работает как генератор стробов. При одновременном включении Кл2 и Kл4 (вход заземляется), а также при определенном подборе опорного напряжения Uоп схема работает как мультивибратор.
На этапе анализа параметров электрическая схема — модель исследуется как аналитически, так и экспериментально. В процессе анализа уточняются ее внешние параметры и характеристики и определяются количественные зависимости изменений этих параметров и характеристик от вариации параметров элементов схемы*. Анализ обычно проводится методами граничных испытаний [1.22, 1.45], частичных испытаний, наихудшего случая [1.47], математического моделирования па ЭВМ [1.48, 1.49] и другими методами.
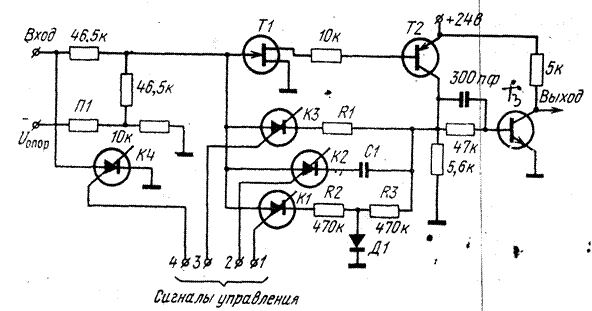
Рис. 1.18. Схема с перестраиваемой структурой.
_____________
*Значения параметров элементов определяются многими факторами, в том числе: технологическим разбросом при изготовлении ИС, влиянием внешней среды (в первую очередь температуры) и старением материалов. Величинами, знаком и вероятностными функциями их распределения обычно задаются, исходя из опытных данных.
Особенности экспериментального моделирования. Прежде всего вызывает затруднение практическая ограниченность вариации параметров схемных элементов. Если резисторы, емкости и индуктивности, параметры которых должны изменяться в заданном диапазоне величин, можно отразить в схеме соответственно потенциометрами, конденсаторами переменной емкости и вариометрами, то гипотетический транзистор с переменными параметрами не имеет практического аналога. Поэтому в процессе эксперимента одни транзисторы (а также другие элементы с нерегулируемыми параметрами) постоянно заменяются в схеме на другие, параметры которых отличаются нужным образом от первых. Это обстоятельство снижает гибкость эксперимента и увеличивает его трудоемкость.
Исследуемая схема-модель должна как можно точнее отражать реальную ИС. Для этого необходимо, во-первых, чтобы элементы схемы-модели были бы точными аналогами соответствующих элементов ИС и, во-вторых, чтобы электрические связи в схеме-модели точно отражали бы связи соответствующих элементов ИС. Реально ни первое, ни второе требование полностью не удовлетворяются, особенно для монолитных (полупроводниковых) ИС.
Резисторы, конденсаторы и транзисторы ИС обладают специфическими паразитными параметрами. В частности, полупроводниковые диффузионные резисторы и конденсаторы имеют паразитную емкость относительно подложки, величина которой зависит от напряжения обратного смещения. Эта паразитная емкость носит распределенный характер и замена её дискретной емкостью является известным приближением. То же самое относится ко всём паразитным ёмкостями, образуемым изолирующими переходами.
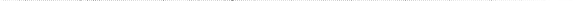 |
Рис. 1.19.Участок полупроводниковой ИС (а), его упрощённая эквивалентная электрическая схема (б), условная эквивалентная схема интегрального транзистора с изолирующим p—n-переходом (в).
Планарный транзистор полупроводниковой ИС часто электрически изолируется от других элементов p—n-переходом (см. рис. 1.19, а). В итоге транзисторная структура получается четырехслойной с тремя p—n-переходами. Эквивалентная схема такой структуры отражает два транзистора: рабочий и «паразитный». Паразитный транзистор в одних случаях улучшаёт импульсные параметры рабочего транзистора, уменьшая накопленный заряд, а в других случаях (в схемах с непосредственными связями) ухудшает их, увеличивая сдвиг входных характеристик при насыщении. Естественно, что указанные ограничения уменьшают гибкость эксперимента. В качестве иллюстрации к сказанному на рис. 1.19, б, в приведены принципиальная схема участка полупроводниковой ИС и его упрощенная эквивалентная схема. В схеме транзистор Tраб, резистор R и два диода Д1 и Д2 являются основными или рабочими элементами, а транзистор Тпар — паразитным. Емкости Сп, С’п и С”п п между подложкой и n-слоем транзисторной, резисторной и диодных структур, а также ёмкости С'p—n и С”p—n между n- и p-слоями резисторной и диодных структур, сопротивления R'п и R”п n-слоев и сопротивления R'п, R”п и R”’п подложки являются паразитными элементами. Ёмкость С'p—n имеет распределённый характер.
Математическое моделирование. Теоретический анализ или моделирование схем обычно производится с помощью ЭВМ. Анализ состоит из следующих последовательных этапов: формализация схемы, составление ее математической модели, разработка алгоритма и программы моделирования, процесс моделирования работы схемы на вычислительной машине, исследование полученных данных. При формализации реальную схему заменяют ее более упрощенным эквивалентом, отражающим главные исследуемые свойства реальной схемы. Математическая модель схемы, как правило, отражает систему дифференциальных уравнений, описывающих протекающие в схеме электрические процессы, а также ограничения, выраженные в виде равенств, неравенств, числовых коэффициентов и т. п.
Алгоритм составляется независимо от конкретного типа вычислительной машины. Программа моделирования работы схемы обычно содержит ряд типовых подпрограмм, отражающих моделирование отдельных сложных элементов (транзисторов и др.). К программе предъявляются требования универсальности, возможности применения для моделирования широкого класса схем, удобства вмешательства на разных этапах моделирования и компактности выдачи конечных результатов. Составление больших программ является сложным и трудоемким процессом.
В настоящее время разработаны стандартные программы моделирования электронных схем на ЭВМ. Примерами таких программ могут служить ПАЭС (программа анализа электронных схем) [1.57] и «Фрехта» (программа расчета и анализа частотных характеристик линейных аналоговых схем) [1.58].
В программе ПАЭС предусматривается расчет переходных процессов схемы, статистический анализ статических и динамических характеристик схемы и расчет схемы на предельный случай. В ее состав входит внешняя программа-диспетчер, цифровая модель схемы и комплекс подпрограмм цифрового моделирования. Общая структура ПАЭС представлена на рис. 1.20. В ПАЭС входит серия типовых подпрограмм: подпрограммы расчета параметров нелинейных элементов (транзистора, диода и др.), подпрограммы определения входных импульсов и выходных параметров различного класса схем, подпрограмма интегрирования дифференциальных уравнений по методу Эйлера с автоматическим выбором шага интегрирования, подпрограмма выработки случайных чисел и другие. Включение в работу тех или иных подпрограмм в нужной последовательности, показанной на рис. 1.20 строками, осуществляется внешней программой. Для типовых алгоритмов анализа схем определенного класса ведущая программа остается неизменной. Автоматизация программирования с помощью создания подпрограмм упрощает процесс подготовки задачи к решению и позволяет более экономно использовать емкость памяти машины. Цифровая модель программируется заново для каждой конкретной схемы.
Процесс получения математической модели схемы в виде системы дифференциальных уравнений несложен; он состоит из ряда формальных процедур, описанных в литературе. Рассмотрим порядок получения математической модели транзистора, используемой при цифровом моделировании интегральных схем. Все существующие его модели получены на основе использования известных уравнений непрерывности и переноса, а также принятия ряда известных допущений[1.59].

Рис. 1.20. Общая структура ПАЭС (программы анализа электронных схем)
Эквивалентная схема p—n—p-транзистора приведена на рис. 1.21. Этой схеме соответствует следующая система дифференциальных уравнений:
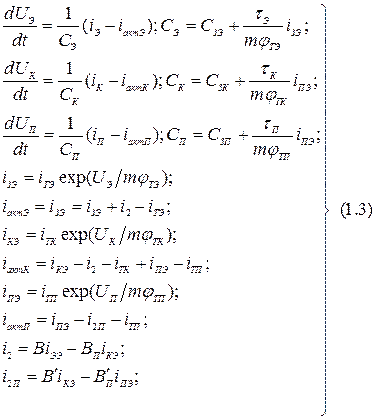

Рис. 1.21. Эквивалентная схема транзистора.
Индексы «э», «к» и «п» относят соответствующую величину к переходу эмиттер—база, коллектор—база и подложка—коллектор; 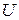 — падение напряжения на переходе;
— падение напряжения на переходе; 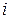 — выходной ток транзистора;
— выходной ток транзистора; 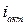 — активная составляющая тока через переход;
— активная составляющая тока через переход; 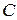 — емкость перехода, включающая зарядную и диффузионную составляющие;
— емкость перехода, включающая зарядную и диффузионную составляющие; 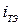 ,
, 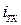 ,
, 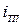 , —тепловые токи переходов;
, —тепловые токи переходов; 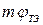 ,
, 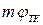 ,
, 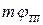 —температурные потенциалы переходов;
—температурные потенциалы переходов; 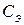 ,
, 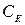 ,
, 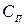 — зарядные емкости переходов;
— зарядные емкости переходов; 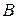 ,
, 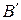 ,
, 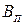 ,
, 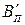 — коэффициенты передачи тока соответственно от эмиттера к коллектору, от коллектора к эмиттеру, от базы к подложке и от подложки к базе;
— коэффициенты передачи тока соответственно от эмиттера к коллектору, от коллектора к эмиттеру, от базы к подложке и от подложки к базе; 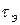 ,
, 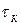 ,
, 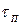 —
—
Дата добавления: 2015-08-26; просмотров: 3446;
