Тема 3 Гидростатическое давление и его свойства

Рассмотрим произвольный объём жидкости (рис. 5, а), находящийся в равновесии под действием внешних сил. Рассечём этот объём какой-либо плоскостью и мысленно отбросим часть, находящуюся с одной стороны от этой плоскости. Для сохранения условия равновесия её действие на оставшуюся часть заменим какой-то равнодействующей силой F. Если на секущей плоскости выделить элементарную площадку Dw, то на неё будет действовать часть равнодействующей силы DF. При уменьшении площади Dw до нуля предел отношения 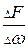называется гидростатическим давление р в данной точке жидкости.

Сжимающее напряжение в покоящейся жидкости называется гидростатическим давлением:

р = 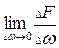(3.1)

или

р = 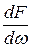. (3.2)

Гидростатическое давление характеризуется тремя основными свойствами.

1. Гидростатическое давление направлено нормально к поверхности, на которую оно действует и создаёт только сжимающие напряжения.

Действительно, в жидкости практически не возникают растягивающие напряжения, а если она находится в покое, то в ней нет и касательных напряжений. Не может давление действовать и на площадку под углом, отличающимся от 90⁰. В этом случае давление можно было бы разложить на нормальное и касательное (рис. 5, б). А касательные напряжения могут возникнуть только при движении жидкости. Поэтому в рассматриваемом случае давление может быть только нормальным к площадке и создавать только сжимающие напряжения.

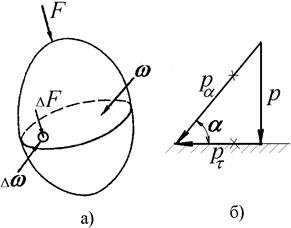
Рисунок 5

2. В любой точке жидкости гидростатическое давление одинаково по всем направлениям р_x = р_y = р_z = р_n.

Для доказательства этого свойства выделим в рассматриваемом объёме жидкости призму с основанием в виде треугольника АВС (рис. 6, а) и заменим действие объёма жидкости вне призмы на её боковые грани соответствующими силами. Так как призма находится в равновесии, то многоугольник (в данном случае треугольник) этих сил замкнут (рис. 6, б). Треугольник сил подобен треугольнику АВС и из закона подобия следует, что

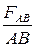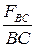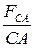= = . (3.3)

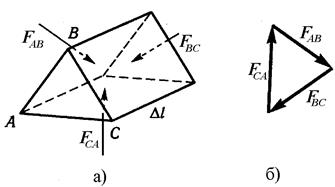
Рисунок 6

Разделим все члены этого равенства на длину призмы Dl:

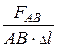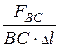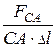= = . (3.4)

Произведения в знаменателях этого выражения представляют площади соответствующих граней призмы. Если размеры АВ, ВС, СА и Dl будут стремиться к нулю, то в соответствии выражением (3.1) получим

р_АВ = р_ВС = р_СА = р. (3.5)

Так как ориентация граней призмы была принята произвольно, то следует считать доказанным положение о равенстве давления в одной точке по всем направлениям р_x = р_y = р_z = р_n.

Выражением второго свойства гидростатического давления является закон Паскаля: давление на свободную поверхность (внешнее давление) передаётся во все точки покоящейся жидкости без изменений.

3. Гидростатическое давление в точке зависит только от её положения в пространстве р = f(x, y, z).

Давление является скалярной величиной, а сила давления – вектор.

В единицах SI давление измеряется в паскалях (Па):

1 Па = 1 .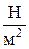

Паскаль связан с другими единицами измерения давления следующими соотношениями:

1 атм. (физическая атмосфера) = 101325 Па = 760 мм рт. ст.;

1 ат (техническая атмосфера) = 1 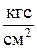= 9,81 × 10⁴ Па;

1 бар = 1 × 10⁵ Па;

1 мм вод. ст. = 1 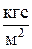= 9,81 Па;

1 мм рт. ст. = 1 Торр = 133,3224 Па.