На критическую силу
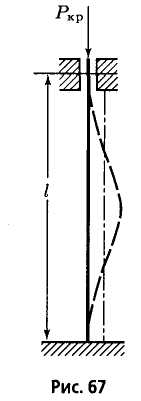
Вывод формулы Эйлера осуществлен для бруса с шарнирно закрепленными концами. Тем не менее эта формула имеет универсальный характер, не зависит от способа закрепления бруса и через коэффициент п учитывает число полуволн синусоиды, которые укладываются на его длине. Применим, например, эту формулу для определения критической силы бруса с заделанными концами (рис. 9.6). Как видим, число полуволн изогнутой оси в этом случае п = 2 и, следовательно, критическая сила при данных опорных устройствах равна
 . (9.3)
. (9.3)
Этот результат можно переписать в виде
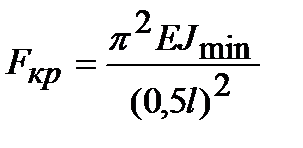 . (9.4)
. (9.4)
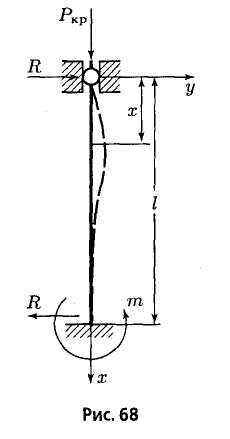
Рассмотрим пример определения критической силы в случае, когда брус изгибается не по целому числу полуволн синусоиды (рис. 9.7) – брус, защемленный одним концом и шарнирно опертый другим.
Данный случай представляет собой статически неопределимую систему. Со стороны шарнирной опоры возникает горизонтальная реакция опоры R.
Изгибающий момент в произвольном сечении бруса будет равен  , а дифференциальное уравнение упругой линии будет иметь вид:
, а дифференциальное уравнение упругой линии будет иметь вид: 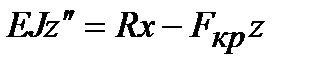 , или
, или 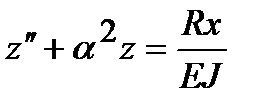 .
.
Общее решение этого уравнения имеет вид:
 .
.
Используя условия на концах бруса, выразим постоянные А и В через R. При х = 0 прогиб z = 0, следовательно, В = 0. При х = l угол поворота сечения равен нулю, поэтому z'(l) = 0.
Из этого условия получаем
 ,
,
и уравнение изогнутой оси приобретает следующий вид:
 .
.
Условие z (l) = 0 будет выполнено, если
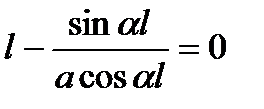 .
.
Отсюда получаем следующее трансцендентное разрешающее уравнение для определения величины a: 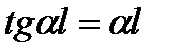 .
.
Наименьший корень этого уравнения определяет первую критическую силу. Это уравнение решается методом подбора или графически. Наименьший, отличный от нуля, корень этого уравнения al = 4,493 = 1,43p.
Принимая al = 1,43p, получаем следующее выражение для критической силы
 . (9.5)
. (9.5)
Проведя подобный вывод формулы для критической силы применительно к брусу, защемленному с одной стороны (рис. 9.8), получаем следующее выражение:

| Fкр |
| Fкр |
| z |
| z |
| Fкр |
| z(x) |
Рис. 9.6 Рис. 9.7 Рис. 9. 8
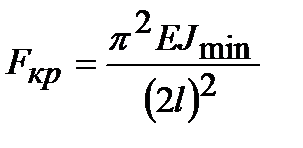 . (9.6)
. (9.6)
Сопоставляя формулы критической силы для бруса, закрепленного различным образом, легко видеть, что все они имеют одинаковое строение. Обобщая их, запишем формулу Эйлера в виде:
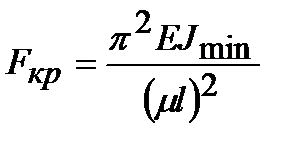 .
.
Здесь m = 1/n величина, обратная числу полуволн п синусоиды, по которой изогнется брус. Постоянная mназывается коэффициентом приведения длины, а произведение ml – приведенной длиной бруса. Случай шарнирного закрепления концов бруса называется основным.
| Fкр |
| Fкр |
| Fкр |
| Fкр |
| Fкр |
| m=1 |
| m=2 |
| m=0,5 |
| m=0,7 |
| m=0,5 |
| Рис. 9.9 |
Таким образом, критическая сила для любого случая закрепления бруса может быть вычислена по формуле для основного случая с заменой действительной длины бруса его приведенной длиной.
Дата добавления: 2015-08-21; просмотров: 826;
