Пределы применимости формулы Эйлера
Формула Эйлера описывает упругое поведение материала под нагрузкой. Это следует из того факта, что в нее входит модуль упругости Е.
Таким образом, применение формулы Эйлера ограничено предельным напряжением sпц, т.е. лишь в тех случаях, когда потеря устойчивости наступает в упругой области деформирования материала:
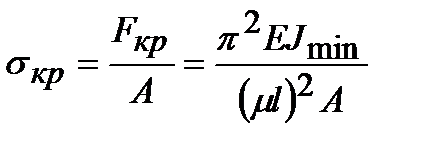 .
.
Обозначая 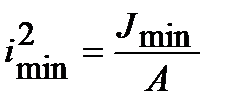 , где imin – радиус инерции сечения, получим
, где imin – радиус инерции сечения, получим  .
.
Величина  называется гибкостью стержня и зависит только от геометрических размеров и способа закрепления стержня.
называется гибкостью стержня и зависит только от геометрических размеров и способа закрепления стержня.
Таким образом, условие, что критические напряжения не должны превышать предела пропорциональности, можно записать в виде
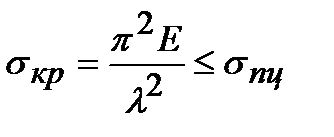 .
.
Для того чтобы выполнялось это условие, значение гибкости должно быть больше предельного значения
 .
.
Как видно из формулы, 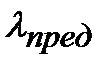 зависит только от свойств материала и для каждого материала ее величина может быть вычислена (табл. 9.1). Для малоуглеродистой стали, имеющей
зависит только от свойств материала и для каждого материала ее величина может быть вычислена (табл. 9.1). Для малоуглеродистой стали, имеющей  МПа и Е=2,1× 105 МПа, формулой Эйлера можно пользоваться при гибкости стержня большей, чем
МПа и Е=2,1× 105 МПа, формулой Эйлера можно пользоваться при гибкости стержня большей, чем
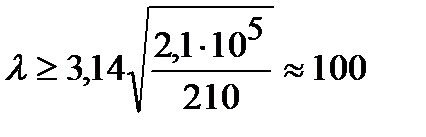 .
.
Для других материалов значения предельных гибкостей сведены в табл. 9.1.
Таблица 9.1
| Материал | λпред | а, МПа | b, МПа |
| Ст.2, Ст.3 | 1,14 | ||
| Сталь 45 | 3,26 | ||
| Чугун | |||
| Дерево | 29,3 | 0,194 |
Если гибкость стержня меньше предельной гибкости, то формула Эйлера дает большую погрешность и не может быть использована (рис. 9.10).
| Рис. 9.10 |
| sкр |
| l |
| lт |
| lпред |
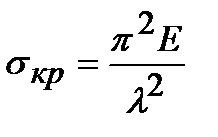
|

|
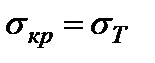
|
| sпц |
 , потеря устойчивости происходит при напряжениях, превышающих предел текучести
, потеря устойчивости происходит при напряжениях, превышающих предел текучести  , поэтому расчет на устойчивость выполняется с помощью эмпирической формулы, предложенной профессором Петербургского института путей сообщения Ф. Ясинским (1902 г.):
, поэтому расчет на устойчивость выполняется с помощью эмпирической формулы, предложенной профессором Петербургского института путей сообщения Ф. Ясинским (1902 г.):
 ,
,
где а и b – эмпирически найденные для каждого материала коэффициенты (табл. 9.1).
Величина критической силы Fкр определяется умножением критических напряжений на площадь поперечного сечения 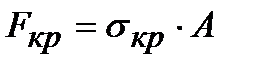 .
.
Для коротких стержней, гибкость которых l < lт , где lт – гибкость стержня, определенная из условия sкр = sт, потеря устойчивости не происходит и поэтому расчет на устойчивость не выполняют.
Дата добавления: 2015-08-21; просмотров: 989;
