Сигналов

Все физические величины по сути дела являются аналоговыми. Когда мы говорим об аналоговой величине, мы говорим, во-первых, о том, что сигнал непрерывно меняется во времени и, во-вторых, о том, что сигнал может принимать любое значение (целое, рациональное, иррациональное). Еще до того как был создан компьютер, люди могли проводить вполне определенные математические операции с аналоговым сигналом.

Из всех физических аналоговых величин (это может быть температура, освещенность, напряжение, напряженность электрического поля) можно выделить одну, например, напряжение. Это связано с тем, что практически любую физическую величину, используя определенные датчики, можно свести к электрической величине.

Сопротивление. Величина сопротивления не является постоянной. На нее могут влиять разные факторы. Например, мы можем говорить о термосопротивлении. Это означает, что величина сопротивления R= R(T). Если мы хотим измерить температуру, можно взять сопротивление и, измеряя его величину, можно сказать какую температуру мы имеем. Магнитосопротивление. Его величина R= R(B) зависит от индукции магнитного поля. Есть фотосопротивление – сопротивление, величина которого зависит от освещенности, т.е. от энергии, приходящейся на единицу поверхности.

Поэтому, когда мы будем говорить об аналоговой величине, мы будем говорить о напряжении.

Закон Ома связывает U, R, I.

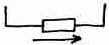
U= I* R

При передаче сигнала по проводам, мы должны учитывать, что любой проводник определенной длины имеет некоторую индуктивность L и емкость С.

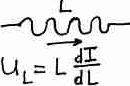
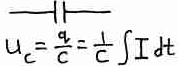
Зная как связаны U и токи на L и C мы можем говорить о том, что будет происходить в любой цепи, состоящей из L, C и R.

Закон Киргофа для полной цепи (ЗСИ): Есль в замкнутую цепь включен источник посторонней ЭДС , то при перемещении единичного положительного заряда по этой цепи, мы должны совершать рботу и, сумма работ, которые совершаются, должна быть равна внешней ЭДС.

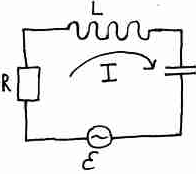
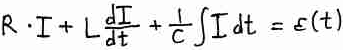
– это ОДУ II порядка. На это уравнение нужно наложить начальные условия. Например, можно задать напряжение в момент времени t= 0 и в момент времени t = ∞, и решить это уравнение.

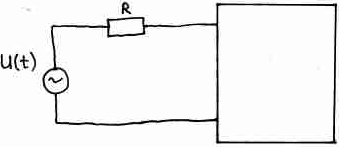
Нам известна величина напряжения на входе. Что мы получим на выходе, зависит от того, какие частоты содержит U(t). В зависимости от этого, мы можем сказать про линию, соединяющую передатчик с приемником, что, либо это линия с сосредоточенными параметрами, либо, что это линия с распределенными параметрами. От этого будут принципиально меняться условия распространения сигнала.

Мы можем оценить весь спектр сигнала U(t).

Пусть на входе сигнал меняется U = U₀∙sinωt. Можно определить длину волны для этого сигнала

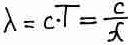
Например, если частота f = 1 ГГц, то λ = 30см.

Сравним длину волны λ с длиной линии l.

l >> λ. По линии напряжение меняется. Это линия с распределенными параметрами. Погонная индуктивность (индуктивность длины линии) и погонная емкость.

l << λ. На длине линии напряженность поля остается постоянной. Это линия с сосредоточенными параметрами. Она обладает вполне определенной емкостью C, и вполне определенной индуктивностью L. Большую роль играет емкость (если речь идет о не очень длинных линиях). Потому, что емкость проводника длиной 1 м в воздухе составляет несколько десятков пФ. Так, что это существенная величина, и ее надо учитывать в первую очередь.

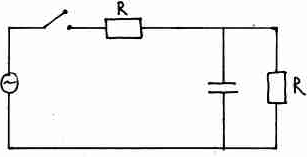
Здесь возникает уравнение Киргофа.

В отличие от сопротивления, индуктивность и емкость – параметры энергоемкие. Это означает что, если конденсатор заряжен, то он обладает энергией

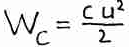
Энергия индуктивности

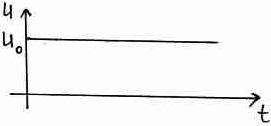
Замкнем ключ в момент t = 0. До того, как ключ был замкнут на конденсаторе напряжения не было, и его энергия была равна 0. Напряжение на конденсаторе через очень большой промежуток времени после того, как был замкнут ключ, будет равно

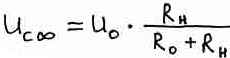
Напряжение на конденсаторе не может сразу вырасти от 0 до этой величины. Если есть внутреннее сопротивление, то не может быть тока зарядки конденсатора больше, чем напряжение U деленное на внутреннее сопротивление. Мощность источника ограничена. В связи с этим конденсатор будет заряжаться постепенно.

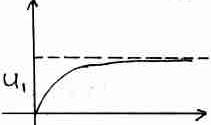
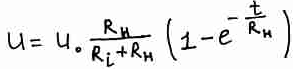
При t = 0 напряжение равно 0.

Примерно те же рассуждения можно провести для учета индуктивности, но получим более сложный закон.

При передаче аналогового сигнала – напряжения по каким-то цепям, с ним происходит изменение. Сигнал на приемнике сильно отличается от сигнала на входе. Всегда ли это так, или можно как-то уменьшить это влияние.

Возьмем линию с распределенными параметрами. Она имеет некоторые погонную индуктивность и погонную емкость. Распространение сигнала по этой линии будет другим. подадим на вход длинной линии гармонический сигнал ε = ε₀∙sinωt