Волновая функция
Состояние микрочастицы (характеристики её движения, взаимодействия с другими частицами и т.д.) полностью задаётся функцией, которую называют волновой функцией и обозначают Y (пси-функция).
Переходя к описанию движения частиц в квантовой механике, сформулируем ряд её постулатов, лежащих в основе теории. Первый постулат квантовой механики гласит: состояние частицы в квантовой механике описывается волновой функцией 
, являющейся функцией пространственных координат и времени. Физико-математический аппарат, разработанный в квантовой механике, позволяет, проводя некоторые операции над волновой функцией Y,получать полную информацию о движении микрочастицы.
Статистический смысл волновой функции.
Невозможность задать состояние микрочастицы указанием в любой момент времени её координат и скорости и отказ от траекторного способа описания движения приводят к вероятностному способу описания движения микрочастицы. Это означает, что в квантовой механике, описывая состояние микрочастицы, следует указать способ определения вероятности обнаружения частицы в различных точках пространства в данный момент времени.
В 1926г. Макс Борн предложил следующий вероятностный смысл волновой функции: квадрат модуля волновой функции определяет плотность вероятности обнаружения частицы в момент времени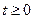 
в точке пространства 
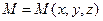с координатами 
:
.
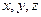Это соотношение можно преобразовать к виду:
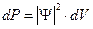или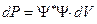 
,
где dP - вероятность того, что для заданного квантового состояния частицы в некоторый момент времени мы обнаружим частицу в некоторой малой области пространства, объём которой dV. Поэтому для нахождения вероятности того, что частица находится в некоторой области V надо вычислить интеграл: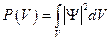 
или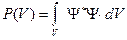 
.
Следовательно, если частица не может находиться в области V, то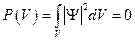 
.
Т.к.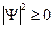 
, то это равенство возможно при 
, т.е.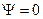 
в этой области V. Если частица обязательно находится в области V, то 
.
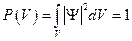Следовательно, квадрат модуля волновой функции должен быть интегрируемой функцией по этой области.
Замечание. Вероятность того, что частица находится в какой-то определённой точке, равна нулю, т.к. в этом случае объём соответствующей области нулевой.
Дата добавления: 2015-08-21; просмотров: 1153;