Принципы изостазии

Наблюдения силы тяжести на земной поверхности показали, что горные массивы притягивают гораздо слабее, чем следовало бы, если исходить из расчетов притяжения видимыми массами. С другой стороны, впадины океанов должны создавать меньшие аномалии вследствие недостатка масс по сравнению с возвышенностями суши. Однако и здесь оказалось, что наблюдаемые аномалии значительно выше расчетных.

Эти факты привели к созданию в конце прошлого века теории изостазии, которая была изложена почти одновременно и независимо друг от друга в 1851 г. английскими геодезистом Праттом и в 1855 г. астрономом Эри. Напомним основные ее положения: согласно теории изостазии, отдельные глыбы земной коры находятся в гидростатическом равновесии и как бы плавают в вязкой массе подстилающей магмы. При этом избыток масс на поверхности компенсируется недостатком их внизу.

По теории Пратта блоки коры имеют разную плотность и высоту. Чем выше блок, тем меньше его средняя плотность. Компенсация массы различных блоков коры предположительно осуществляется где-то в мантии на некотором уровне Т (рис. 21). Таким образом, если r₁ и r₂ – плотности континентального блока, r₃ – плотность океанического блока, Н – высота блока над уровнем моря, Р – глубина моря, то, согласно Пратту, имеют место следующие равенства:

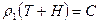(IV.30)

и

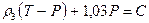; С = const, (IV.31)

откуда

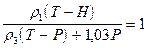(IV.32).

При Н = 0 найдем постоянную r₀Т = С; r₀ = 2,67 г/см³, откуда С = = 2,67Т.

С учетом формулы (IV.30) и полученного значения для С найдем Т:

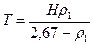. (IV.33)

Рис. 21. Модели изостазии: а – по Пратту; б – по Эри

Если компенсация осуществляется на нулевом уровне (Т = 0), то это соответствует нулевой плотности столба, возвышающегося над уровнем моря, т. е. внешние массы гор и материков равны нулю. На языке редукций это соответствует поправке за свободный воздух. Таким образом, редукция Фая соответствует изостатической компен­сации на уровне моря, при этом массы, расположенные под точкой наблюдений, опускаются на уровень моря и конденсируются в бесконечно тонкий слой.

Если компенсация осуществляется на бесконечности (Т = ¥), что имеет место при 2,67 – r₁ = 0, т. е. избыточных масс нет, то надземные массы притягивают плотностью. Это соответствует редукции Буге, где весь избыток масс отнесен за счет притяжения слоя плотностью 2,67 г/см³, лежащего выше уровня моря, что адекватно опусканию избыточных масс под уровень моря и «размазыванию» их на бесконечно большую глубину. Таким образом, редукции Фая и Буге по существу являются предельными изостатическими редукциями. Они показывают, что уровень компенсации Т лежит где-то между нулем и бесконечностью. Американский геофизик Хейфорд показал, что вероятная глубина изостатической компенсации разноплотностных блоков земной коры равна 122 км. В более поздних работах она оценивалась от 96 до 102 км.

По гипотезе Эри земная кора имеет всюду одинаковую плотность, но разную высоту блоков и как бы плавает в более тяжелом субстрате (см. рис. 21). Следовательно, разность плотности субстрата (магмы) r и плотности земной коры r₀ у Эри – величина постоянная r – r₀ = Dr. Глубина погружения блока определяется законом Архимеда – более высокий блок имеет больший корень в магме, чем блок менее высокий. Условие равновесия запишется в виде: r₀В = rb. Здесь В – мощность коры блока; b – глубина погружения его в магму. Отсюда нетрудно видеть, что

.

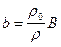Несмотря на различные предпосылки в схемах Пратта и Эри, математически они не отличаются друг от друга, массы блоков до некоторой фиктивной границы компенсации Т оказываются равны.

Основной формулой для вычисления изостатической редукции является формула для притяжения кругового цилиндра на точку, лежащую на его оси на некоторой высоте Н:

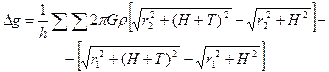(IV.34)

Подбор глубины компенсации в формуле (IV.34) по известным значениям плотности r, высоты рельефа Н и радиусов выбранных зон r₁ и r₂ осуществляется минимизацией величины Dg до нуля. Считается, что приблизительной оценкой наличия изостатической компенсации области является положительный знак аномалии Фая и отрицательный аномалии Буге. Одинаковый знак аномалии служит указанием на изостатическую некомпенсированность области.

Правомочность выделения постоянной плотности для коры в схемах изостазии как будто подтверждается линейной связью между мощ­ностью коры М и высотой рельефа Н на суше: М = М_о + KН. Наличие такой корреляции указывает на заметный плотностный контраст между корой и верхней мантией (до границы М). Аналогичная связь обнаруживается и для аномалий Буге, а также только для суши: М = М_о+КDg_Б. Свыше 95% гравитационного эффекта в радиусе 20 км реализуется притяжением масс, расположенных в земной коре, и лишь 75% – в радиусе 167 км. Таким образом, трудно говорить об изостатическом равновесии, когда для малых блоков практически вся аномалия Dg вызвана массами в коре, а для более чем градусных площадей сказывается кривизна поверхности Земли, и сколько здесь приходится на изостазию, сколько на притяжение сферического слоя, сказать трудно.

Венинг-Мейнис также указал на искусственность схем Пратта и Эри, ибо в природе нет разделения коры на независимо скользящие относительно друг друга блоки. Он предложил свой вариант изостазии в виде изгибающейся пластинки, края которой, будучи связанными со стабильными участками коры, не подчиняются законам гидростатики. Тем не менее перисфера, следуя сокращающемуся радиусу Земли, садится не в более плотную мантию, как это имеет место в моделях изостазии Пратта и Эри, а в лучшем случае в занятое летучими и легкоплавкими пространство астеносферы. В этом смысле механизм изостазии в масштабе Земли отсутствует, что и подтверждается многочисленными исследованиями, согласно которым примерно 40 – 50% площади поверхности Земли является изостатически нескомпенсированной (Джеффрис, 1960). Однако иногда изостатические аномалии, по мнению некоторых исследователей, предпочтительнее аномалий Фая, и особенно Буге, так как они не вносят больших искажений в наблюденное поле искусственным перемещением и добавлением фиктивных масс, искажающих геоид. Например, как следует из формулы «насып­ной» (условной) редукции Буге для моря, Dg_Б = 0,0418(2,67 – 1,03)Н = = 0,0685Н, на каждую 1000 м глубины «аномалия Буге» увеличивается на 68·10^{-5 м}×с^-2 (68 мгал). Это значительно больше величин для сухопутных измерений на тех же широтах.

Большие положительные изостатические аномалии (более 10×10^‑5 м×с^-2) приурочены главным образом к возвышенностям, отрицательные – к континентальным впадинам, щитам и океаническим котловинам. В среднем эта картина сходна с данными о форме геоида. Кроме того, осредненные по 5-градусным квадратам аномалии Фая и изостатические аномалии оказываются одинаковы по знаку и близки по величине. Это особенно хорошо видно при сравнении областей с большими изостатическими аномалиями. Отсюда следует, что осредненные по большим площадям аномалии Фая близки действительному распределению поля силы тяжести на поверхности Земли. В свою очередь этот факт служит указанием на существование глубины компенсации, близкой к нулевой, т. е. аномалии действительно в основном обусловлены плотностными неоднородностями в верхах перисферы и в меньшей степени в астеносфере и тем более глубже. Замечательно, что рифтовые хребты характеризуются довольно значительными (около 10×10^{-5 м}×с^-2 и более) положительными изостатическими аномалиями и аномалиями Фая, а котловины по обе стороны от них – отрицательными.

Вышеизложенное согласуется с данными изучения ундуляции геоида. На рис. 22 приведена карта превышений геоида над поверхностью эллипсоида со сжатием .

Величина ундуляции составляет +78¸-112 м. Максимальная амплитуда «рельефа» геоида равна 180 м. Ундуляции геоида не совпадают с распределением континентов и океанов. Зоны отрицательных значений W охватывают восточную наиболее глубоководную половину Тихого океана. Северную Америку и северо-западную часть Атлантики, а также Индийский океан и Центральную Азию. Тем не менее наиболее глубокие отрицательные значения W приходятся на океанические бассейны, а положительные – на континентальные области и западную окраину Тихого океана. Это свидетельствует о том, что ундуляция геоида вызвана плотностными неоднородностями масс, лежащих за пределами возможных структурных и петрографических различий континентальной и океанической коры. Следовательно, карта геоида отражает характер разуплотнения вещества на уровне глубже 35 – 40 км. Отсюда мы получаем подтверждение в гравитационных данных сделанному выше выводу о том, что зонам современных опусканий соответствует наибольший недостаток масс – глубже границы М. Минимумы геоида совпадают с областями рифтовых хребтов и с прилегающими к ним котловинами, а также щитами континентов. Районам океана, характеризующимся максимумами высот геоида, соответствуют наиболее глубокие положительные региональные аномалии силы тяжести в свободном воздухе (аномалия Фая). Районам минимумов высот геоида соответствуют наиболее глубокие отрицательные региональные аномалии Фая. Однако имеются и исключения. Таким образом, ундуляции геоида дают заметный вклад в аномальное гравитационное поле как континентов, так и океанов; этот вклад достигает в среднем величины ±50×10^{-5 м}×с^-2.

По данным американской спутниковой съемки SE-III и судовым наблюдениям, минимумы Dg преимущественно приурочены к докембрийским платформам и глубоководным котловинам. Однако в целом однозначная интерпретация невозможна. Поле весьма мозаично и отражает плотностную гетерогенность верхов твердой перисферы.

Статистический анализ данных гравиметрических измерений как на суше, так и на море показывает, что аномалия Фая коррелирует с рельефом поверхности Земли или с погребенным под тонким слоем рыхлых осадков рельефом кристаллического фундамента (базальтово­го – в океанах). Поэтому в большинстве случаев по наблюденным локальным или региональным аномалиям в свободном воздухе практически невозможно судить о плотностных соотношениях перисферы без предварительного учета влияния топографии. Осреднение по 1´1° или 5´5° квадратам позволяет исключить сравнительно мелкие неровности и ошибки измерений, а также влияние коротковолнового рельефа. Это, в свою очередь, позволяет оценить аномальный эффект регионального порядка для сравнительно большого интервала глубин вплоть до астеносферного слоя. Выше было показано, что осредненные по крупным площадям аномалии Фая приближаются к высотным спутниковым и изостатическим аномалиям, что в первом приближении указывает на преимущественно коровое происхождение основной части аномального поля Dg. Следовательно, для получения представлений о плотностном состоянии крупных регионов на большей глубине мы должны пользоваться осредненными значениями поля в редукции Фая.

Сопоставление данных сейсмики о положении границы М с аномалиями в редукции Буге вскрывает еще одну закономерность. Существует и прямая, точнее, линейная зависимость между глубиной границы М и величиной Dg. Однако эта зависимость реализуется лишь в так называемых изостатически скомпенсированных областях, т. е. в областях, где выступы рельефа земной поверхности компенсируются соответствующими утолщениями коры снизу. Из этого правила исключаются океанические области, где за подошву коры берутся сейсмические границы 7,4 – 7,8 – 8,1 км/с, которые на самом деле являются лишь промежуточными коровыми границами (Орлёнок, 1980, 1982). Аномалии Буге на суше конформны поведению границы М. Осредненные по 3´3° квадратам аномалии Буге увеличиваются линейно с уменьшением средней высоты рельефа приблизительно на 95·10^{-5 м}×с^-2 на 1 км высоты суши. По Н. П. Грушинскому, зависимости аномалий Буге и высоты рельефа суши от глубины залегания границы М подчиняются следующему линейному закону: М = М_о + КDg_Б; М = М_о¢+КН, где Н – средняя высота рельефа; Dg_Б – среднее значение аномалии Буге; М – мощность коры; К и М_о – коэффициенты, подлежащие определению. Например, для всей Земли М_о¢ = 35,0; К¢ = 0,073; М_о = 35,6; К = = 5,05. Только для суши М_о = 37,5; К = 0,059; М¢ = 37,7; К¢ = 1,84. Только для морей М_о = 30,8; К = 0,062; М₀¢ = 28,1; К¢ = 3,35. Из этого следует главный вывод, что гравитационный эффект масс, распределенных в земной коре до границы М, значительно превышает эффект масс, распределенных глубже этой границы. Поэтому аномалии Буге в основном характеризуют (в региональном плане) совместное влияние мощности коры и особенности изменения плотности пород в ее пределах. Аномалия Фая менее чувствительна к таким изменениям, так как не учитывает промежуточные массы в этом диапазоне глубин. Таким образом, аномалия Буге более чувствительна к флуктуациям мощности и плотности коры, а аномалия Фая – к флуктуациям поверхностного рельефа. Изостатическая аномалия свободна от этих влияний, характеризует промежуточный уровень компенсации (между нулем и бесконечностью) и, как правило, имеет более сглаженный характер с амплитудой порядка ± 10×10^{-5 м}×с^-2.

В общем случае плотностные неоднородности верхних слоев перисферы (до границы М) уверенно определяются гармониками сферических функций, начиная с n ³ 6. Низшие гармоники (n £ 2) могут дать информацию о неоднородностях нижней мантии и внешнего ядра. Это, в частности, следует из того, что ширина аномалии силы тяжести в первом приближении пропорциональна глубине залегания аномалиеобразующих масс, хотя в ней, как и в магнитном поле, присутствует эффект влияния горизонтальной мощности аномалиеобразующего тела. Иными словами, чем шире аномалия, тем глубже расположены возмущающие массы. Дюрбаум (1974) рассмотрел этот вопрос детально и показал, что большинство вычислительных схем определения вер­хних кромок аномальной гравитирующей массы сводится (для сравнительно простых форм) к определению половины ширины аномалии.

С учетом всего сказанного изостатическое редуцирование следует рассматривать как один из способов интерпретации гравиметрических наблюдений, соответствующих той или иной теоретической модели коры. Изостатические же аномалии будут характеризовать осредненную плотность верхов перисферы в региональных масштабах, но никак не их динамическое состояние. Для реализации последнего необходимы надежные сейсмические данные о положении границ раздела по всей тектоносфере. Однако таких данных ни по одному из регионов мы пока еще не имеем.