Приливы
Луна, находясь в поле тяготения Земли (и обе планеты – в поле солнечного притяжения), оказывает воздействие на массу самой Земли. Вследствие больших размеров и массы Земли относительно ее спутника (rл/rз = 0,27; mл/mз = 1,2×10-2) различные точки Земли под влиянием поля тяготения Луны будут испытывать неодинаковые возмущения по отношению к центру массы. Величина этих возмущений зависит от положения тел. В зените (z = 0) или в надире (z = 180°) притяжение максимальное: 0,166 см/с2 для Луны и 0,061 см/с2 – для Солнца; при положении тел в горизонте (z = 90°) притяжение тел минимальное: ‑0,083 см/с2 для Луны и -0,003 см/с2 для Солнца; нулевые значения достигаются при z = 54°44ґ и z = 125°16ґ. Величина статического прилива составляет для Луны от 35,6 до -17,8 см, для Солнца – от 16,4 до ‑8,2 см. Следовательно, размах амплитуды лунных приливов равен 53,4 см, солнечных – 24,6 см; суммарное влияние составляет 78 см (Мельхиор, 1975). Полученные значения теоретической высоты статического прилива верны для жидкой модели Земли. В абсолютно твердой земле никаких деформаций поверхности не происходило бы. Данные непосредственных наблюдений показывают, что высота реального прилива составляет 65 %, или около 51 см от теоретического. Иными словами, земной шар отличается от жидкой модели и от абсолютно твердого тела. Это хорошо согласуется с предыдущими выводами относительно вязкости и жесткости.
В массовом отношении полученный гравитационный эффект равен Dg/g » 0,2/106, т.е. масса в 1 т (106 г) изменяется в результате лунно-солнечного притяжения на 0,2 г. На первый взгляд это незначительная величина, однако если сравнить ее с массой всей Земли, перисферы или гидросферы, наиболее подверженных приливным возмущениям, то получаются внушительные цифры: изменение массы Земли составит 11,948×1020 г (Мз = 5,974×1027 г), перисферы – 1018 г (Мп = 9×1025 г), гидросферы – 3,3×1017 г (Мг = 1,64×1024 г). Если учесть, что эти гигантские массы смещаются в теле Земли регулярно, периодически, на протяжении многих миллионов лет, то становится более понятной роль гравитационного взаимодействия Земли, Луны и Солнца в эволюции протовещества планеты. Представление величины 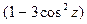 приливного потенциала
приливного потенциала
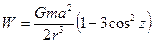 (IV.38)
(IV.38)
в сферической системе координат позволяет разложить его на три лапласовы составляющие, которые получили название зональных, секториальных и тессеральных волн (рис. 24).
Рис. 24. Приливы на поверхности Земли:
а – секториальные; б – тессеральные; в – зональные
Распределение секториальных волн прилива происходит в широтном направлении. Узловые линии, или фронт волны, имеют меридиональное простирание – от полюса до полюса. Максимальная амплитуда прилива достигается на экваторе в полосе шириной от 10° с.ш. до 10° ю.ш. с постепенным уменьшением к полюсам, где функция W принимает нулевое значение (рис. 25). Положительное значение W, соответствующее области прилива, функция принимает в зените и надире, отрицательное, соответствующее отливу, – в квадратурах. Доминирующая секториальная волна обозначается индексом M2. Она имеет полусуточный период (12 ч 25 мин). Этот прилив вызывает внутреннее трение за счет волн, обрушивающихся на протяженную линию побережий Тихого, Атлантического и Индийского океанов, и ответственен за некоторую часть векового замедления скорости вращения Земли. Одновременно с волной M2 появляются еще две лунные волны – N2 и L2 с периодами, близкими к периоду доминирующей волны.
| Рис. 25. Изменение амплитуды вертикальной составляющей основных приливных волн в зависимости от широты (по Мельхиору, 1975): K1, O1, Р1 – тессеральные суточные приливные волны; M2, S2, N2 – секториальные полусуточные волны |
Тессеральный прилив имеет более сложный фронт: узловые линии располагаются по меридиану и экватору. При этом максимум волны
достигается на широтах 45° с.ш. и 45° ю.ш. На экваторе и полюсах функция W = 0. Тессеральному приливу соответствуют главная фаза М1 и две близкие по периоду волны К1 и О1. Их период равен звездным суткам. Несимметричность тессерального прилива относительно экватора и различная амплитуда его в северном и южном полушариях обусловливают прецессию и нутацию земной оси за счет изменения главного момента инерции Земли.
Зональный прилив (см. рис. 24) зависит только от широты. Его фронтом являются 35° с.ш. и 35°16ґ ю.ш. Максимальная амплитуда достигается на полюсах. Поскольку склонение Луны изменяется с периодом 27,321 средних звездных суток, период зонального прилива составляет 14 суток. Зональный прилив определяет сжатие Земли. Перераспределение масс на полюсах и экваторе (прилив на полюсах ведет к образованию отлива на экваторе) приводит к изменению экваториального и полярного моментов инерции, что вызывает изменение главного момента инерции и периодические колебания скорости вращения Земли (Мельхиор, 1975).
В результате вращения узлов лунной орбиты с периодом Т0 = = 18,613 года образуется дополнительная волна прилива, амплитуда которой сравнима с амплитудой месячного прилива. Сложение ее с главной волной зонального прилива приводит к настолько сильному перераспределению масс в теле Земли и перисфере, что это находит выражение в периодичности землетрясений и вулканизма Тихоокеанского подвижного пояса. В частности, прогноз 19-летних циклов составляет до 94 % для сильных землетрясений с магнитудой М ³ 7 и глубиной очагов 0 – 600 км, а также для мощного вулканизма.
Кроме перечисленных волн имеются аналогичные им солнечные приливные волны несколько меньшей амплитуды, которые, складываясь с лунными, усиливают их.
Гармонический анализ только месячной серии приливных наблюдений позволяет выделить еще целый ряд волн. В частности, по разложению Дудсона получается 115 секториальных полусуточных, 158 тессеральных суточных, 99 зональных долгопериодных и 14 секториальных третьесуточных волн. Взаимодействие всех этих фаз приводит к сложнейшим взаимным перемещениям возмущающих масс вещества в теле Земли и на поверхности. При этом наибольшей амплитуды перемещения достигнут, очевидно, в разуплотненных зонах астеносферы и внешнего ядра. Это должно способствовать ускорению термогравитационной дифференциации и самих химических реакций. В периоды сизигий в результате сложений лунно-солнечного потенциала тяготения процессы станут резко усиливаться. Перемещение вещества будет происходить из зоны квадратур. Таким образом, земное вещество в разуплотненных зонах благодаря приливному взаимодействию на протяжении всей истории Земли находилось в постоянном и сложном движении.
Как следует из выражения для приливного потенциала (IV.38), где величина 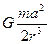 определяет амплитуду, а
определяет амплитуду, а 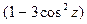 – фазу, амплитуда возмущений уменьшается по мере удаления от поверхности Земли к ее центру, так как в числителе стоит квадрат земного радиуса, а в знаменателе – куб расстояния от спутника. Следовательно, приливное взаимодействие наибольшей амплитуды достигает в верхах перисферы Земли, а также в астеносфере и «жидком» ядре. Это и находит свое выражение в корреляции вулканизма и землетрясений с периодами лунно-суточных приливов.
– фазу, амплитуда возмущений уменьшается по мере удаления от поверхности Земли к ее центру, так как в числителе стоит квадрат земного радиуса, а в знаменателе – куб расстояния от спутника. Следовательно, приливное взаимодействие наибольшей амплитуды достигает в верхах перисферы Земли, а также в астеносфере и «жидком» ядре. Это и находит свое выражение в корреляции вулканизма и землетрясений с периодами лунно-суточных приливов.
Эволюция системы Земля – Луна
Уменьшение скорости вращения Земли на 2 с за 105 лет устанавливается астрономическими измерениями. Это замедление не является флуктуирующим или случайным. Анализ эфемеридного времени, в частности, по солнечным затмениям шумерских, вавилонских, египетских и других наблюдений, выполненных более 2000 лет назад и имевших внутреннюю согласованность, дает ту же величину – 2 с за 105 лет (Мельхиор, 1975). Палеонтологические наблюдения ископаемых кораллов палеозойского возраста обнаруживают заметные различия в количестве суточных поясков по сравнению с современными кораллами. Один такой поясок соответствует световому дню, в течение которого он наращивается. По количеству поясков удается установить продолжительность года в различные геологические эпохи. Эти результаты приведены в табл. IV.1
Таблица IV.1
Изменение продолжительности года и суток в фанерозое
(по П. Мельхиору, 1975)
| Период | Время, млн. лет | Продолжительность | |
| года, сут | суток, ч | ||
| Настоящее время | 365,26 | 24,00 | |
| Меловой | 370,33 | 23,67 | |
| Пермский | 384,10 | 22,82 | |
| Каменноугольный | 387,50 | 22,62 | |
| Девонский | 398,75 | 21,98 | |
| Силурийский | 407,10 | 21,53 |
Из табл. IV.1 видно, что, начиная с силура, т.е. за 440 млн. лет, продолжительность суток увеличилась на 2,47 ч и возрастание происходило линейно со средней скоростью, составляющей 1,9 с за 105 лет.
Таким образом, три независимых источника дают один порядок закономерного и прогрессивного уменьшения скорости вращения Земли вокруг своей оси. Линейный характер этого процесса на протяжении фанерозоя свидетельствует об его устойчивости и отсутствии каких-либо катаклизмов. Вследствие уменьшения скорости вращения Земли происходит обмен моментами количества движения с Луной. В результате уменьшалась скорость вращения Луны вокруг своей оси и одновременно возрастало расстояние между Землей и Луной. В итоге этой эволюции в будущем можно ожидать прекращения вращения Земли вокруг своей оси и система Земля – Луна, достигнув минимума энергии, будет вращаться вокруг центра масс подобно гантели: планеты будут всегда обращены друг к другу одной стороной. В ходе приливного торможения при достижении равенства моментов орбитального удаления Луны и скорости вращения Земли спутник может начать обратное вращение вокруг своей оси. Например, из 13 спутников Юпитера 9 вращаются в прямом направлении, а 4 – в обратном. Систему, видимо, близкую к гантели, имеют Меркурий и Солнце, ибо, находясь ближе всех планет к светилу, Меркурий испытывает наиболее мощное гравитационное торможение вращения со стороны солнечных приливов.
Если в первом приближении предположить, что скорость приливного замедления вращения Земли сохранялась на протяжении всей ее геологической истории, то, экстраполируя ее на время 4,5×109 лет, получим скорость вращения протопланеты, равную 1,77 ч. Современная скорость вращения Луны вокруг своей оси в 27 раз меньше скорости вращения Земли. Следовательно, можно предположить, что Луна в первый раз остановила свое вращение 4,5×109/27 = 1,66 ×108 лет назад. Ввиду малого момента инерции спутника относительно момента инерции Земли спутник после остановки должен был начать обратное вращение под влиянием поля тяготения Земли, продолжая при этом удаляться от нее.
Поскольку не вся энергия гравитационного взаимодействия расходуется на торможение (часть ее рассеивается на тепло), полученная цифра может быть несколько иной. Тем не менее период 170 млн. лет совпадает с циклами тектонической активности фанерозоя.
По расчетам П. Мельхиора (1975), замедление угловой скорости вращения Земли составляет около +4,8×10-22 с-2, а замедление скорости удаления спутника, согласно третьему закону Кеплера, – 3,6 см/год. Энергия современных приливов равна 8,1×1019 Дж/год. Среднее современное расстояние спутника от Земли равно 3,844×1010 см. Если удаление шло также равномерно, как и замедление вращения, что, очевидно, взаимосвязано, то при скорости 3,6 см/год за 4,5×109 лет имеем расстояние, равное 1,62×1010 см. Следовательно, сразу после образования планет спутник находился на расстоянии в 2,4 раза меньше современного. Однако этот расчет сделан без учета эволюции Мирового океана, дающего наибольший вклад в процесс замедления скорости вращения (приливное торможение).
Приливные силы разрушают спутник на расстоянии ближе 2,34 радиуса, т.е. 14908,14 км от Земли. Это так называемый предел Роша. Герстенкорн предположил, что 1400 – 1600 млн. лет назад Луна была захвачена Землей и находилась на расстоянии немного большем предела Роша (Ботт, 1974). Однако в докембрийской геологии это событие не нашло отражения, ибо оно соответствовало бы образованию катастрофических приливов как в теле Земли, так и ее спутника. Значит, есть основания предположить, что современная скорость приливного торможения не всегда была таковой, а на протяжении длительного времени имела много меньшее значение. Но, согласно полученным нами (Орлёнок, 1980, 1982) данным, крупные и глубокие океанские бассейны появились на Земле лишь в конце палеогена, т.е. 25 – 30 млн. лет назад. Существовавшие же на протяжении большей части докайнозойской истории небольшие мелководные бассейны типа современных шельфовых морей исключали возможность получения сильного приливного торможения.
С учетом сказанного оценим ближайшее расстояние, которое занимала Луна в прошлом по отношению к Земле. За 30 млн. лет Луна удалилась на расстояние 3,6 см/год´30×106 лет = 108×106 см, т.е. на 1080 км. В докайнозойскую эпоху вследствие слабого приливного торможения скорость удаления ее была по меньшей мере на порядок ниже современной 0,36 см/год´4,5×109 лет = 1,62×109 см, т.е. удаление составило 16200 км. Следовательно, Луна и Земля в момент своего образования находились всего на 17 – 20 тыс. км ближе, чем сейчас, что не могло существенно повлиять на величину тогдашних твердых и жидких приливов.
Таким образом, наибольшее приливное торможение Земля испытала в конце первой крупной фазы океанизации, т.е. в конце палеогена – начале неогена. Но при большей скорости вращения земной шар должен был иметь сжатие с полюсов и, следовательно, большее вздутие по экватору. Из наблюдений эволюции спутника Земли было установлено, что планета имеет избыток экваториального вздутия, равный 70 м. Этот избыток не соответствует современной скорости вращения. Он возник в доокеанскую эпоху (25 – 30 млн. лет назад) при большей, чем современная, скорости вращения планеты. Очевидно, Земля не находится в состоянии гидростатического равновесия. Подобное запаздывание в приобретении ею гидростатического равновесия при постепенном приливном уменьшении скорости вращения позволяет оценить вязкость нижней мантии в 1025 Па×с (Ботт, 1974), а это исключает возможность существования конвекции в мантии и оболочке Земли, что подтверждается к тому же и их существенной вертикальной и горизонтальной неоднородностью. Следовательно, конвекционный механизм плитовой тектоники построен на широких допущениях и предположениях, в природе реально неизвестных.
Рассмотрим теперь эффект быстрого вращения протопланеты. Согласно выводам Пуанкаре, существует некоторый предел между угловой скоростью вращения планеты и ее массой, при переходе которого центробежные силы вращения превзойдут силы внутреннего притяжения и планета рассыплется. Это условие имеет вид:
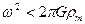 , (IV.39)
, (IV.39)
где rm – средняя плотность планеты.
Приведем оценку для Земли. Так как
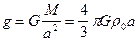 ,
,
то, подставляя это значение в неравенство (IV.39) и предположив 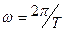 , получим:
, получим:
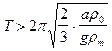 .
.
После подстановки численных значений a, g, r0, rm находим:
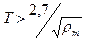 . (IV.40)
. (IV.40)
Таким образом, в неравенство (IV.40) входит только средняя плотность планеты, т.е. размеры не играют роли. Для современной Земли Т = = 24 ч, rm = 5,52 г/см3, следовательно, Т = 24>1,15 и условие Пуанкаре выполняется полностью и с большим запасом. Это значит, что современная Земля представляет собой консолидированное тело. Однако для периода вращения протопланеты имеем
 .
.
Одинаковый порядок сил тяготения и центробежной силы ранней Земли указывает на весьма слабое сцепление масс протовещества, даже с поправкой на меньшую первоначальную среднюю плотность (rm = 3,34 г/см3). В этих условиях выполнение предположения Герстенкорна привело бы к краху планеты и спутника: сильный прилив вытянул бы протовещество, что могло привести к их слиянию. Если бы Луна обладала такой же скоростью первоначального вращения, как и Земля, то неравенство Пуанкаре имело бы в этом случае вид: Т = = 1,77>1,15. Величины тоже предельные.
В итоге мы должны признать, что они позволяют оценить характер и направленность эволюции системы Земля – Луна. Все имеющиеся данные указывают на то, что первоначальная скорость вращения протопланет была больше современной, а их гравитационное взаимодействие заметно сильнее вследствие более близкого расположения их на орбите.
В этих условиях становятся понятными причины быстрого разогрева планет, образование термореакционных зон внутри Земли и раннее образование коры на Луне. Приливные перемещения частиц протовещества планет способствовали быстрому выделению огромных количеств тепла и разогреву планет. Судя по тому количеству тепла, которое дают оставшиеся долгоживущие уран, торий, калий и другие элементы, нет основания ожидать, что этот разогрев мог иметь место только за счет распада короткоживущих изотопов (Орлёнок, 1980).
Дата добавления: 2015-06-27; просмотров: 1443;
