Работа трехразрядного сумматора. Схема.
Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.
Для того чтобы получить многоразрядный сумматор, достаточно соединить входы и выходы переносов соответствующих двоичных разрядов. Схема соединения одноразрядных сумматоров для реализации четырехразрядного сумматора приведена на рисунке 10.
Рисунок 10. Принципиальная схема многоразрядного двоичного сумматора
Одноразрядные сумматоры практически никогда не использовались, так как почти сразу же были выпущены микросхемы многоразрядных сумматоров. Полный двоичный четырехразрядный сумматор изображается на схемах как показано на рисунке 11.
Рисунок 11. Условно-графическое изображение полного двоичного многоразрядного сумматора
Естественно, в приведенной на рисунке 10 схеме рассматриваются только принципы работы двоичных сумматоров. В реальных схемах никогда не допускают последовательного распространения переноса через все разряды многоразрядного сумматора. Для увеличения скорости работы двоичного сумматора применяется отдельная схема формирования переносов для каждого двоичного разряда. Таблицу истинности для такой схемы легко получить из алгоритма суммирования двоичных чисел, а затем применить хорошо известные нам принципы построения цифровой схемы по произвольной таблице истинности.
 Многоразрядный сумматор
Многоразрядный сумматор
Таким образом, в общем случае для каждого разряда необходима логическая схема с тремя входами ai, bi, Ci и двумя выходами Si, Ci+1. Такая схема и есть полный сумматор. Ее можно реализовать с помощью двух полусумматоров. Далее рассмотрим таблицу функционирования. pi, gi, ri — промежуточные величины.
Таблица функционирования многоразрядного сумматора:
| ai | bi | Ci | pi | gi | ri | Si | Ci+1 |
Для сложения двух многоразрядных двоичных чисел на каждый разряд необходим один полный сумматор. Только в младшем разряде можно обойтись полусумматором. На рисунке приведена схема, предназначенная для сложения двух четырехразрядных чисел А и В. Эта схема выпускается в интегральном исполнении. В ее младшем разряде также используется полный сумматор, чтобы иметь возможность наращивания разрядности схемы.
Многоразрядный сумматор с последовательным переносом:
Время выполнения операции в сумматоре с последовательным переносом намного больше времени сложения в одноразрядном сумматоре. Действительно, сигнал переноса С4только тогда может принять истинное значение, когда будет установлено правильное значение С3. Такой порядок выполнения операций называется последовательным переносом (Ripple Carry).
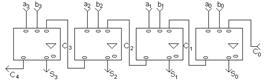
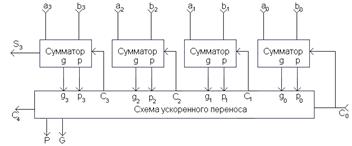
Чтобы уменьшить время операции сложения многоразрядных чисел, можно использовать схемы параллельного переноса (Carry look-ahead). При этом все сигналы переноса вычисляются непосредственно по значениям входных переменных. Для сигнала переноса i-го разряда справедливо соотношение:
Ci+1 = aibi + (ai ⊕ bi)Ci = gi + piCi
Величины gi, ri вычисляются в качестве промежуточных результатов и в полном сумматоре. Следовательно, их получение не требует дополнительных затрат. Сигнал giвырабатывается тогда, когда в данном разряде перенос происходит из-за комбинации входных переменных ai, bi. Поэтому его называют функцией генерации переноса. Сигнал piпоказывает, передается ли полученный в младшем разряде сигнал переноса Ci дальше. Поэтому он называется функцией распространения переноса.
Таким образом, можно вывести следующие формулы для вычисления сигналов переноса:
C1 = g0 + p0C0
C2 = g1 + p1C1 = g1 + p1g0 + p1p0C0
C3 = g2 + p2C2 = g2 + p2g1 + p2p1g0 + p2p1p0C0
C4 = g3 + p3C3 = g3 + p3g2 + p3p2g1 + p3p2p1g0 + p3p2p1p0C0
Хотя полученные выражения достаточно сложные, время формирования сигнала переноса в любой разряд с помощью вспомогательных функций определяется только временем задержки распространения сигнала на двух элементах. Эти функции реализуются специальным комбинационным устройством — схемой ускоренного переноса.
Схема сумматора с параллельным переносом приведена на рисунке. На другом рисунке изображена схема устройства параллельного переноса в группе из четырех разрядов. Эта схема реализует полученную ранее систему уравнений.
3-хразрядный сумматор можно синтезировать из полусумматора и 2-хразрядного сумматора. Полусумматор будет складывать младшие разряды. После его переполнения сигнал с выхода переноса пойдёт на вход переноса сумматора.

9.4. 3-разрядные сумматоры
Определенным образом соединяя полусумматоры и полные сумматоры друг с другом, получают устройства, одновре- одновременно выполняющие сложение нескольких двоичных разря- разрядов. Устройство, схема которого показана на рис. 9.7, складывает 3-разрядные двоичные числа. Числа-слагаемые обозначены А2Л1А0 и В2В1В0. Сигналы, соответствующие значениям разряда единиц в слагаемых, поступают на входы сумматора разряда единиц (полусумматора). Входными сигналами для полного сумматора разряда двоек являются сигнал переноса с выхода полусумматора (подается на вход Сщ) и значения А± и В1 разряда двоек в слагаемых. Далее сумматор четверок складывает А2, В2 и сигнал переноса с выхода сумматора двоек. На двоичном выходе устройства (показанном в правом нижнем углу рис. 9.7) индицируется искомая двоичная сумма. В резуль- результате сложения двух 3-разрядных двоичных чисел может по- получиться 4-разрядное число, поэтому на индикаторе суммы имеется дополнительный разряд восьмерок. Обратите вни-внимание, что этот разряд связан с выходом (Со) сумматора четверок.
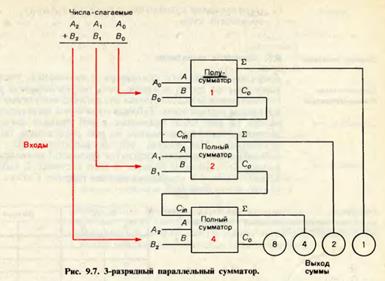
Логика работы рассмотренного 3-разрядного суммато- сумматора ничем не отличается от последовательности операций, выполняемых при сложении вручную (сложение однораз- одноразрядных чисел плюс перенос в следующий разряд). Однако электронный сумматор выполняет эти операции во много раз быстрее. Еще раз отметим, что в многоразрядных сум- сумматорах полусумматоры используются только для сложе-сложения в разряде единиц; во всех других разрядах используют- используются полные сумматоры. Рассмотренный нами 3-разрядныйсумматор называется параллельным сумматором. В параллельном сумматоре информационные биты Есех разрядов поступают на входы одновременно. Результат (сумма) появляется на выходе практически мгновенно. Па- Параллельный сумматор на рис. 9.7 относится к классу комби- наиионных логических схем. Для фиксации данных на вхо- входах и выходах сумматоров обычно используются раз-различные дополнительные регистры.
Соты с одинаковыми частотами должны быть разнесены в пространстве на расстояние не меньше чем 3R, а второе требование гласит, что С/I должен быть не меньше 12 дБ, при наличие в сети 6 сот одинаковыми частотами. Определить С/I если известны следующие параметры: , , , (для открытой местности), .
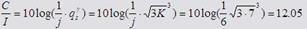
Дата добавления: 2015-04-10; просмотров: 16694;
