Проверка данных на аномальность
Любая исследуемая совокупность, наряду со значениями признаков, сложившихся под влиянием факторов, непосредственно характерных для анализируемого объекта, может содержать и значения признаков, полученных под воздействием иных факторов, не характерных для изучаемого объекта. Такие значения резко выделяются и, следовательно, использование методологии статистического анализа без изучения аномальных наблюдений приводит к серьезным ошибкам. Обычно аномальные значения можно обнаружить визуально, при помощи графического представления временных рядов, но, прежде чем «подправить» обнаруженные таким образом значения ряда, их необходимо подвергнуть дальнейшему количественному и качественному анализу.
Следует различать понятие аномальности для:
v Одномерной выборки невременного характера;
v Одномерной выборки типа ”Временной ряд”;
v Многомерной выборки.
Пример 1: Одномерная выборка Х невременного характера
Х – мощность пласта (в метрах)
| 1,31 | 0,94 | 1,61 | 1,42 | 1,25 |
| 1,31 | 1,15 | 1,02 | 1,92 | 1,29 |
| 1,28 | 1,14 | 2,38 | 1,92 | 0,9 |
| 1,34 | 1,12 | 1,8 | 1,38 | 1,27 |
| 1,3 | 0,99 | 0,98 | 1,42 | 1,22 |
| 1,5 | 0,98 | 1,27 | 1,34 |
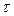 – Критерий проверки на аномальность
– Критерий проверки на аномальность
1. Расчет числовых характеристик ( 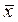 ; Dв ; sв ; S2 ; S ) для всей выборки.
; Dв ; sв ; S2 ; S ) для всей выборки.
2. Вычисление для каждого значения выборки 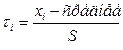
3. Проверка условия 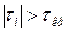 (7)
(7)
где 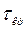 – критическое значение, которое находится по таблице (файл ”Образец зад. 2”). Возможны варианты:
– критическое значение, которое находится по таблице (файл ”Образец зад. 2”). Возможны варианты:
· если условие (7) не выполняется, то точка  считается не аномальной;
считается не аномальной;
· если условие (7) выполняется, то точка  считается аномальной. В этом случае ее удаляют из выборки, а затем получившуюся в результате выборку вновь подвергают проверке на аномальность.
считается аномальной. В этом случае ее удаляют из выборки, а затем получившуюся в результате выборку вновь подвергают проверке на аномальность.
v Пример 2:Одномерная выборка У типа ”Временной ряд”
Будем понимать аномальность уровней временного ряда как существенное, достаточно локализованное по времени (или другой дискретной переменной ряда) отличие от остальной совокупности наблюдений. Предлагаем следующую классификацию аномальных наблюдений, применительно к признакам, характеризующих (или связанных) с процессами метановыделения.
Аномальность первого рода (рис.2) проявляется в виде сильного изменения уровня показателя – скачка или спада – с последующим приблизительным восстановлением предыдущего уровня. Аномальность этого типа, как правило, наблюдается в очень узкой окрестности некоторых точек временной оси. 
Рис.2
На рис.2, характеризующем процесс метановыделения на шахте Молодогвардейская в 17 лаве в течение месяца, аномальным наблюдением первого рода может оказаться точка под номером 8.
Аномальность второго рода (рис.3) – это нетипичное поведения исследуемого показателя на заметном интервале временной оси.
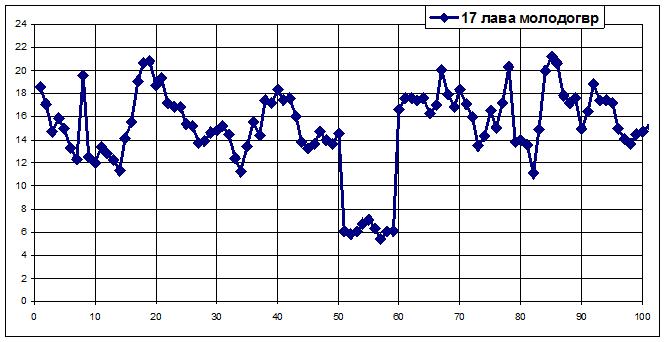
Рис.3
На рис.3, представляющем процесс метановыделения в той же лаве в течение 100 дней, возможный интервал аномальных наблюдений второго рода находится между 50-той и 60-той точками (или сутками).
Для диагностики аномальных наблюдений динамических рядов разработаны различные критерии, например, метод Ирвина [3Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В.Федосеева. М.: ЮНИТИ, 1999.] Для всех или только для подозреваемых в аномальности наблюдений вычисляется величина 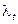 :
:
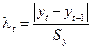 , (8)
, (8)
где 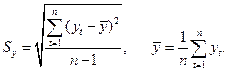 . (9)
. (9)
Если рассчитанная величина 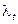 превышает табличный уровень, то уровень
превышает табличный уровень, то уровень 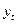 считается аномальным. Аномальные наблюдения необходимо исключить из временного ряда и заменить их расчетными значениями (самый простой способ замены – в качестве нового значения принять среднее из двух соседних значений).
считается аномальным. Аномальные наблюдения необходимо исключить из временного ряда и заменить их расчетными значениями (самый простой способ замены – в качестве нового значения принять среднее из двух соседних значений).
Таблица Критические значения параметра 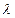 .
.
| Количество наблюдений n | 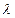
| |
| P=0,95 | P=0,99 | |
| 2,8 | 3,7 | |
| 2,2 | 2,9 | |
| 1,5 | 2,0 | |
| 1,3 | 1,8 | |
| 1,2 | 1,7 | |
| 1,1 | 1,6 | |
| 1,0 | 1,5 | |
| 0,9 | 1.3 | |
| 0,8 | 1.2 |
Дата добавления: 2015-06-27; просмотров: 3238;
