Сложение элементов симметрии

Сочетание нескольких элементов симметрии не является произвольным, а подчиняется строгой геометрической закономерности, которая заключается в том, что при наличии двух элементов симметрии фигура обладает и третьим элементом симметрии, равнодействующим первым двум.

Равнодействующим называют элемент симметрии, действие которого приводит фигуру в то же положение, что и последовательное действие двух других элементов симметрии. Например, в правильной четырёхугольной призме (рис. 2.11) плоскость симметрии Р₂ является равнодействующей другой плоскости симметрии Р₁ и оси симметрии L₄.

С другой стороны, L₄ - является равнодействующей плоскостей симметрии Р₁ и Р₂.

Так как два элемента симметрии всегда дают третий, им равнодействующий, то в кристаллических многогранниках возможны либо только один элемент, либо больше двух.

Нахождение по двум элементам симметрии им равнодействующего называется сложением элементов симметрии.

Познакомимся с основными теоремами сложения элементов симметрии.

Теорема 1. Линия пересечения двух плоскостей симметрии является осью симметрии, равнодействующей этим плоскостям.

Теорема 2. Если через ось симметрии проходит плоскость симметрии, то через ту же ось должна проходить вторая плоскость симметрии под углом 90⁰ к первой.

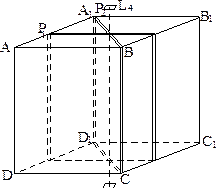
Следствие. Если через ось симметрии n-го порядка проходит плоскость симметрии, то всего через эту ось должно проходить n плоскостей симметрии.

Пусть число плоскостей симметрии равно m, т.к. каждая плоскость, проходящая через L_n повторяется через 180⁰, число плоскостей симметрии должно быть равно

m=180/( 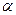/ 2)=360 / 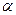=n,

где n - порядок данной оси симметрии.

Теорема 3. При наличие оси симметрии чётного порядка (L_2n) и центра инверсии (С), перпендикулярно к оси через центр инверсии проходит плоскость симметрии (Р), равнодействующая данной оси и центра инверсии.

Теорема 4. При наличии плоскости симметрии и центра инверсии на ней фигура всегда обладает осью симметрии чётного порядка, проходящей через центр инверсии перпендикулярно к плоскости симметрии.

Теорема 5. При наличии оси симметрии чётного порядка и перпендикулярной к ней плоскости симметрии всегда присутствует центр инверсии, равнодействующей оси и плоскости симметрии.

Все три последние теоремы являются взаимообратными.

Следствие. При наличии центра инверсии число плоскостей симметрии равно сумме всех чётных осей симметрии, причём каждая плоскость симметрии перпендикулярна соответствующей оси симметрии.

Например, в кубе имеется С, 3L₄, 4L₃ и 6L₂. Так как сумма чётных осей симметрии равна 9, то всего куб должен иметь 9Р.

Теорема 6 (Теорема Эйлера). Равнодействующей двух пересекающихся осей симметрии является третья ось симметрии, проходящая через точку пересечения первых двух.

Следствие. При наличии оси симметрии n - го порядка (L_n) и перпендикулярной к ней оси симметрии второго порядка (L₂) имеется всего n осей второго порядка (nL₂), перпендикулярных к L_n и пересекающихся друг с другом под углом 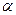/ 2.