Математическое моделирование сорбции ионов меди и кадмия образцами карбонизованной РШ
Для решения практических задач представляет интерес математическое моделирование адсорбции на сорбенте. Модель кинетики сорбции исходит из предположения, что описание гетерогенной системы, включающей сорбент и сорбат, допустимо в рамках модели сплошной среды [137; 138]. Физической предпосылкой для выбора математической модели процесса сорбции является эффект перераспределения массы в одном объеме в ходе сорбирования. Это предопределяет необходимость уточнения модели, а также специфику описания кинетики сорбции.
В данной работе, на примере сорбции ионов тяжелых металлов на карбонизованных образцах рисовой шелухи, представлен метод определения параметров модели, и проведено сравнение экспериментальных и расчетных данных. Математическая модель разработана совместно с к.ф.-м.н. Б.А. Урмашевым.
В оценке сорбентов большое значение имеет кинетика адсорбционного процесса. Для ее изучения были проведены серии экспериментов. Использовался раствор с начальной концентрацией ионов кадмия 0,1 мкг\см3 и ионов меди 5,0 мкг\см3.
Первоначально для этой цели был использован общеизвестный метод статистических моментов (МСМ), практика применения которого в обработке кинетических процессов в разных областях насчитывает не одно десятилетие. Это – гидродинамика, хроматография, адсорбция, фармакокинетика [139-144]. МСМ является альтернативой классическому, порой очень трудоемкому и не всегда реализуемому, способу изучения динамики процессов решением систем дифференциальных уравнений. Чаще всего он используется для определения параметров первого приближения [141] или расчета специфических, присущих данной области знаний, характеристик [140; 142-144].
В качестве анализируемого кинетического процесса был использован:
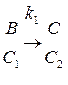 (5)
(5) 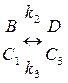 (6)
(6)
где k1, k2, k3 – константы реакций,
C1, C2, C3 – концентрации ионов металла.
Нетрудно заметить, что основным элементом системы является необратимый процесс (5), сочетание которого с обратимой стадией (6) дает возможность получить усложненный вариант. В данном случае под обратимой стадией подразумеваются процессы сорбции-десорбции, непрерывно происходящие до момента установления определенного равновесия.
Введя, согласно методу статистических моментов, следующие обозначения:
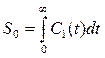 (7),
(7), 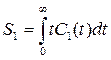 (8),
(8), 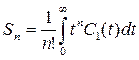 (9),
(9),
где S0 и S1 соответственно нулевой и первый моменты, Sn – момент n-ного порядка, аналитическое решение для самой простой системы (5) можно представить в виде уравнений (10) и (11).
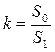 (10)
(10) 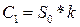 (11)
(11)
Здесь значения Sn, в соответствии с тем, что C=f(τ) для данного случая рассчитывается по уравнению 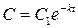 (12), будет равно:
(12), будет равно:
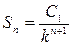 (13),
(13),
где С1 – начальная концентрация иона металла в растворе.
Если система (5) усложняется возможностью обратимого взаимодействия B↔D, тогда для случая (5-6) концентрация рассчитывается по формуле (14).
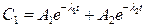 (14),
(14),
где параметры А1 и А2 выражаются в виде уравнений:
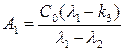 (15),
(15), 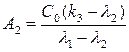 (16)
(16)
λ1,2 – это корень квадратного уравнения, полученного при решении дифференциального уравнения:
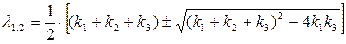 (17)
(17)
Физический смысл λ1,2 заключается в том, что этот коэффициент подразумевает константу скорости распределения ионов металла.
Значения констант скорости k1- k3 и начальной концентрации C1 связаны с Sn следующим образом:
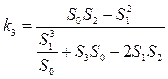 (18),
(18), 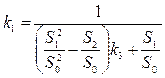 (19),
(19),
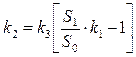 (20),
(20), 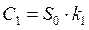 (21)
(21)
Величины Sn для этой системы связаны с зависимостью C-t (12) уравнением (22):
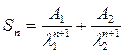 (22)
(22)
Итак, для расчета констант скорости отдельных стадий и начальной концентрации системы с помощью МСМ, выведены уравнения, имеющие аналитическое решение; для проведения расчетов требуются только данные C=f(t) компонента B. Практическая реализация этого метода зависит от возможностей определения базовых элементов МСМ – величин Sn. Особенность функций (10) такова, что с ростом порядка n их значения возрастают многократно относительно исходной величины S0.
Таким образом, большие значения Sn могут быть найдены с очень большими ошибками, вследствие чего значения ki и C1, вычисленные с их помощью, в большинстве случаев не могут быть использованы даже в качестве параметров первого приближения.
Исходя из этого, был использован другой метод определения кинетических параметров [145], структурная основа которого построена по аналогии с МСМ. В качестве базовых элементов, полученных с помощью преобразований Лапласа, предложено использовать функции:
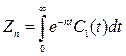 (23)
(23)
Преимущества Zn перед Sn заключаются в том, что с ростом «n» значения Zn уменьшаются, а не растут как в МСМ, то есть ряд S0<S1<…<Sn (24) обращается в Z0>Z1>…>Zn(25)
В связи с вышеизложенным были получены следующие зависимости:
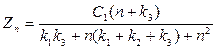 (26)
(26) 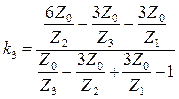 (27)
(27) 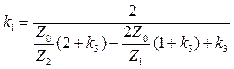 (28)
(28) 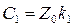 (29)
(29)
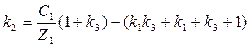 (30)
(30)
Погрешность расчета вычислялась по следующей формуле:
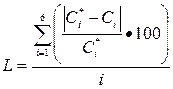 (31),
(31),
где L – погрешность, %;
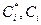 - экспериментальная и расчетная концентрации, мкг/см3.
- экспериментальная и расчетная концентрации, мкг/см3.
Для проведения расчета полученных уравнений была составлена программа на алгоритмическом языке Delphi 7.0. Вычисления проведены при широком варьировании начальных и режимных параметров. Результаты расчетов представлены на рисунках 27, 28 и в таблицах 12, 13.
Таблица 12 – Изменение концентрации ионов кадмия в растворе со временем
| Концент-рация С, мкг\см3 | Время τ, мин | Погрешность измерения L, % | Температура карбонизации Т, °С | |||||
| Ci | 0,1 | 0,0355 | 0,0267 | 0,0242 | 0,0199 | 0,0163 | 5,77 | |
| Cexp | 0,1 | 0,0355 | 0,0291 | 0,0228 | 0,0179 | 0,0176 | ||
| Ci | 0,1 | 0,0250 | 0,0206 | 0,0190 | 0,0161 | 0,0137 | 6,13 | |
| Cexp | 0,1 | 0,0250 | 0,0233 | 0,0169 | 0,0151 | 0,0146 | ||
| Ci | 0,1 | 0,0326 | 0,0201 | 0,0179 | 0,0144 | 0,0117 | 5,81 | |
| Cexp | 0,1 | 0,0326 | 0,0224 | 0,0150 | 0,0152 | 0,0117 | ||
| Ci | 0,1 | 0,0411 | 0,0224 | 0,0153 | 0,0075 | 0,0036 | 9,88 | |
| Cexp | 0,1 | 0,0411 | 0,0273 | 0,0117 | 0,0073 | 0,0039 | ||
| Ci | 0,1 | 0,0275 | 0,0230 | 0,0184 | 0,0117 | 0,0075 | 5,21 | |
| Cexp | 0,1 | 0,0275 | 0,0256 | 0,0158 | 0,0121 | 0,0076 | ||
| Ci | 0,1 | 0,0062 | 0,0021 | 0,0021 | 0,0020 | 0,0019 | 4,86 | |
| Cexp | 0,1 | 0,0062 | 0,0021 | 0,0019 | 0,0023 | 0,0018 | ||
| Ci | 0,1 | 0,0071 | 0,0054 | 0,0041 | 0,0025 | 0,0015 | 6,43 | |
| Cexp | 0,1 | 0,0071 | 0,0064 | 0,0039 | 0,0028 | 0,0014 | ||
| Ci | 0,1 | 0,0018 | 0,0015 | 0,0015 | 0,0015 | 0,0015 | 3,00 | |
| Cexp | 0,1 | 0,0018 | 0,0017 | 0,0015 | 0,0016 | 0,0015 | ||
| Ci | 0,1 | 0,0155 | 0,0079 | 0,0064 | 0,0041 | 0,0027 | 10,87 | |
| Cexp | 0,1 | 0,0155 | 0,0059 | 0,0069 | 0,0035 | 0,0029 | ||
| Примечание: Ci – расчетная концентрация, Cexp – экспериментальная концентрация |
В данной модели константа скорости к2 характеризует общий ход процесса сорбции. Константа к3 показывает скорость процесса обратимой сорбции ионов металла с поверхности углеродного материала, а константа к1 – характеризует процесс необратимой сорбции. Из рисунка 27 видно, что скорость необратимой сорбции ионов кадмия, начиная с 650 ºС, превышает скорость обратимой сорбции. Степень извлечения ионов кадмия при этом ощутимо возрастает.
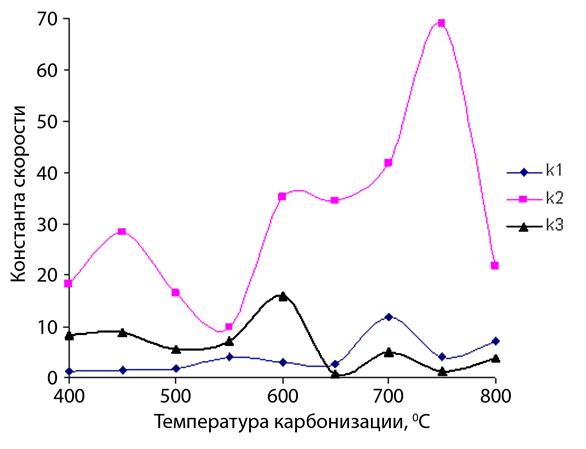
Рисунок 27 – Константы скоростей сорбции-десорбции ионов кадмия в зависимости от температуры карбонизации
Таблица 13 – Изменение концентрации ионов меди в растворе со временем
| Концен-трация, мкг\см3 | Время τ, мин | Погрешность измерения L, % | Температура карбонизации Т, °С | |||||
| Ci | 4,51 | 1,6900 | 1,4955 | 1,3228 | 1,0349 | 0,8097 | 4,55 | |
| Cexp | 4,51 | 1,6900 | 1,6100 | 1,1700 | 1,1000 | 0,8000 | ||
| Ci | 4,80 | 1,4900 | 1,0137 | 0,9492 | 0,8426 | 0,7480 | 5,57 | |
| Cexp | 4,80 | 1,4900 | 1,1300 | 0,8440 | 0,8000 | 0,7900 | ||
| Ci | 4,80 | 1,1000 | 0,6444 | 0,6176 | 0,5766 | 0,5383 | 1,93 | |
| Cexp | 4,80 | 1,1000 | 0,6620 | 0,6020 | 0,5560 | 0,5530 | ||
| Ci | 5,10 | 1,8280 | 1,4420 | 1,3272 | 1,1278 | 0,9583 | 4,00 | |
| Cexp | 5,10 | 1,8280 | 1,5520 | 1,2410 | 1,0690 | 1,0030 | ||
| Ci | 5,10 | 0,2230 | 0,1354 | 0,1144 | 0,0877 | 0,0583 | 7,74 | |
| Cexp | 5,10 | 0,2230 | 0,1450 | 0,1150 | 0,0680 | 0,0650 | ||
| Ci | 5,10 | 0,0770 | 0,0482 | 0,0419 | 0,0316 | 0,0238 | 15,56 | |
| Cexp | 5,10 | 0,0770 | 0,0670 | 0,0290 | 0,0290 | 0,0270 | ||
| Ci | 4,81 | 0,0460 | 0,0349 | 0,0304 | 0,0231 | 0,0176 | 9,65 | |
| Cexp | 4,81 | 0,0460 | 0,0430 | 0,0240 | 0,0220 | 0,0190 | ||
| Ci | 4,81 | 0,1180 | 0,0447 | 0,0329 | 0,0178 | 0,0096 | 14,23 | |
| Cexp | 4,81 | 0,1180 | 0,0600 | 0,0220 | 0,0190 | 0,0100 | ||
| Примечание: Ci – расчетная концентрация, Cexp – экспериментальная концентрация |
Это явление закономерно, т.к. с ростом температуры карбонизации удельная поверхность углеродного сорбента возрастает и ее роль в процессе сорбции, соответственно, тоже. Увеличение значений константы к2 с ростом температуры карбонизации также свидетельствует об этом. Можно предположить, что волнообразный ход кривой к2 указывает на наличие нескольких механизмов сорбции. Так, например, на начальных температурах карбонизации (до 550 ºС) происходит, преимущественно, хемосорбция за счет большого количества свободных радикалов, а с ростом температуры выше 550ºС возрастает роль физической сорбции. Такая же картина наблюдается в случае сорбции ионов меди. Начиная с 550-600 ºС, величина константы к1 превышает значение к3, что сказывается на степени извлечения ионов меди. Как следует из таблиц 12, 13, погрешность расчетов разработанной математической модели составляет ≈ 7%.
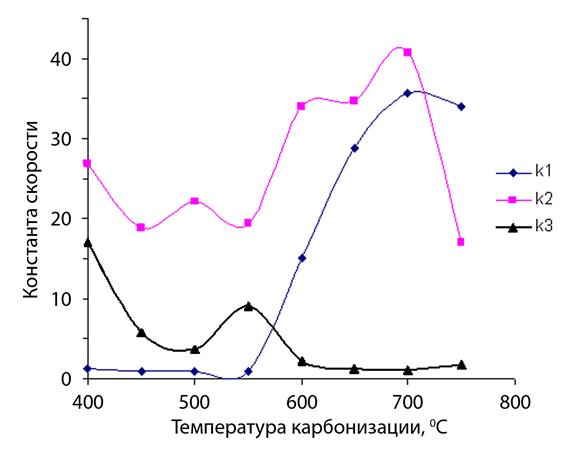
Рисунок 28 – Константы скоростей сорбции-десорбции ионов меди в зависимости от температуры карбонизации
Таким образом, составлена математическая модель, и разработана методика численного расчета, позволяющие выявить основные закономерности протекания процессов сорбции в различные моменты времени при изменении режимных параметров. Анализ полученных данных показывает, что модель правильно описывает изучаемые процессы сорбции. Результаты математического моделирования могут быть использованы для определения кинетики адсорбции ионов металлов на различных сорбентах.
Дата добавления: 2015-06-27; просмотров: 1562;
