Основные положения гемодинамики. Закона Гагена –Пуазейля
На движущийся в сосуде удельный цилиндр крови по закону Ньютона влияет несколько сил (Рис):
1.Движущая-гидростатическая:
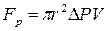 , где:
, где:
pr2=S-площадь цилиндра,
2.Препятствующая- вязкости:
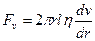 , где:
, где:
S-площадь соприкосновения цилиндра c окружающей жидкостью S=2πrl,
dv/dr-скорость движения жидкости.
Так как, по закону Ньютона на движущуюся равноускоренно жидкость, то:
Fв = -Fд, тогда:
- 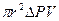 =
= 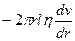 и после алгебраических преобразований и интегрирования:
и после алгебраических преобразований и интегрирования:
- 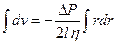 и
и 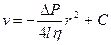 .
.
- С учетом константы интегрирования v=0 при r=R:
- 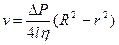 –уравнение параболы.
–уравнение параболы.
Скорость движения жидкости максимально в центре оси.
Объем жидкости (Q) равен интегралу по поверхности вращения этой функции:
- 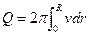 и, подставив сюда значения уравнения параболы, получим:
и, подставив сюда значения уравнения параболы, получим:
- 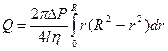 и после алгебраических преобразований и интегрирования:
и после алгебраических преобразований и интегрирования: 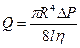 . закон Гагена –Пуазейля: расход крови в сосудах пропорционален градиенту давления и радиусу сосуда в четвертой степени и обратно пропорционален вязкости и длине сосуда.
. закон Гагена –Пуазейля: расход крови в сосудах пропорционален градиенту давления и радиусу сосуда в четвертой степени и обратно пропорционален вязкости и длине сосуда.
- Периферическим сопротивлением является выражение:
- 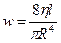
- Оно согласуется с уравнением Гагена –Пуазейля следующим образом:
- 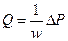
Дата добавления: 2015-06-22; просмотров: 1165;
