Глава 6. Понятие о сопутствующей линии положения

Как известно из курса «Математические основы судовождения», для однозначного определения места судна, его пути и истинной (относительно земли) скорости, когда путь и истинная скорость судна постоянны, необходимо и достаточно иметь четыре разновременно полученные из наблюдений линии положения (изолинии). Каждая такая линия положения связывает одним уравнением четыре параметра, которыми определяется вектор истинной скорости судна: координаты точки приложения этого вектора (текущие координаты места судна), величину скорости и направление линии пути (ПУ).

Предположим, что из наблюдений получены только три разновременные линии положения, например три пеленга. Если использовать метод крюйс-пеленга, то можно иметь лишь счислимо-обсервованное место, на точность которого окажут влияние ошибки счисления. М. Н. Андреев показал, что, имея три разновременные линии положения (одновременность двух из них допустима), можно получить на любой момент плавания, пока судно сохраняет постоянными путь и истинную скорость, еще одну линию положения, на которой находится место судна. Эта линия положения концентрирует в себе всю навигационную информацию от наблюденных разновременных линий положения и от постоянства вектора истинной скорости судна V. Она перемещается вместе с судном и поэтому названа М. Н. Андреевым сопутствующей линией положения (СЛП).

Для того чтобы легче понять сущность сопутствующей линии положения (линии положения особого рода), рассмотрим предварительно два частных случая.

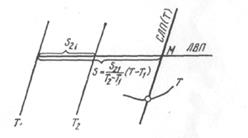
Первый частный случай. Известно обсервованное место судна в момент Т₁. В момент Т₂ из наблюдений получена еще одна линия положения (рис.). Найдем все возможные места судна на некоторый момент Т при условии, что с момента Т₁ судно следует с постоянными, хотя и неизвестными ПУ и V. В дальнейшем это условие подразумевается всегда и специально не оговаривается. Для решения поставленной задачи проложим вначале одну из линий возможных путей судна (ЛВП). Она обязательно начинается в точке Т₁ и пересекает линию положения Т₂. Если судно следовало именно так, то нетрудно рассчитать, где оно окажется в момент Т. Это наглядно показано на рисунке. Очевидно, что если точка М — одно из возможных мест судна на момент Т, то все возможные места судна на этот момент будут находиться на прямой, проходящей через точку М параллельно линии положения представлять собой сопутствующую линию положения для момента Т, т. е. СЛЛ(Т).

Если в момент Т была получена из наблюдений какая-либо изолиния (на рис.— кривая), то точка ее пересечения с СЛП(Т) определит место судна в этот момент. Имея два места судна на разные моменты, легко получить вектор его истинной скорости.

Второй частный случай. В моменты Т₁ и Т₂ получены из наблюдений две параллельные друг другу линии положения (рис.). Найдем все возможные места судна на некоторый момент Т. Для решения поставленной задачи достаточно провести одну из линий возможных путей судна, получить на этой линии точку М (возможное место судна на момент Т) и из этой точки провести прямую, параллельную линиям положения Т₁ и Т₂. Эта прямая будет представлять собой сопутствующую линию положения на момент Т, т.е. СЛП(Т). Если в момент Т из наблюдений была получена какая-либо изолиния (кривая на рис.), то точка ее пересечения с СЛП(Т) определит место судна в этот момент.

В рассматриваемом случае вектор истинной скорости судна получить нельзя. Если бы задача решалась аналитически, то мы имели бы только три уравнения (две линии положения и изолиния), связывающие четыре неизвестных. С помощью этих уравнений можно получить лишь два неизвестных — координаты места судна (точки приложения вектора истинной скорости). В первом частном случае имели бы четыре уравнения (две линии положения и обсервованное место судна, эквивалентное двум уравнениям). Поэтому и графическое построение позволило бы решить задачу полностью.

Перейдем теперь к способу геометрического построения сопутствующей линии положения в общем случае. Предположим, что в моменты Т₁, Т₂ и T_z из наблюдений получены три линии положения, не пересекающиеся в одной точке. Найдем все возможные места судна на некоторый момент Т. За линию возможного пути судна примем каждую из разновременных линий положения поочередно и определим на этих линиях точки М₁, М₂, М₃, в которых может находиться судно в момент Т. В аналитической теории сопутствующих линий положения доказывается, что все эти точки лежат на одной прямой, представляющей собой сопутствующую линию положения — СЛП(Т). В этом можно убедиться, если выполнить построение так, как показано. на рис. принята система обозначений с помощью индексов. Так, например, символ 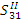означает возможный отрезок линии пути судна между третьей и первой линиями положения, когда за линию возможного пути судна принята вторая линия положения. Получив из наблюдений в момент Т какую-либо изолинию (кривая на рис.), в пе­ресечении ее с СЛП(Т) найдем место судна в момент Т. Имея место судна и еще две линии положения Т₁ и Т₂ или T₁ и T₃ приемом, рассмотренным в первом частном случае, можно определить вектор истинной скорости судна.

Таким образом, СЛП(Т) есть геометрическое место всех возможных мест судна на момент Т при условии, что в течение промежутка времени Т-Т₁ судно шло равномерно и прямолинейно, пересекая полученные из наблюдений разновременные линии положения в правильной последовательности и так, что отрезки линии пути судна между ними были пропорциональны соответствующим промежуткам времени.

Если судно следует постоянным курсом и частота вращения гребных винтов поддерживается постоянной, то и при неизвестных поправке лага, угле дрейфа и элементах течения гипотеза о равномерности и прямолинейности движения судна в промежутке между измерениями навигационных параметров практически справедлива. Следовательно, обсервации по разновременным линиям положения с использованием сопутствующей линии положения свободны от главного источника ошибок — ошибок счисления. Поэтому к такого рода обсервациям целесообразно прибегать во всех случаях, когда нет возможности определить место судна по двум и более одновременным линиям положения.

Вопросы для самоконтроля

1. Что представляет собой сопутствующая линия?

2. Как построить сопутствующую линию?

3. В каких случаях применяется сопутствующая линия для ОМС?