Основные характеристики дисперсных наполнителей
Размер частиц. Когда мы говорим о дисперсном наполнителе или порошкообразном состоянии вещества, то мы знаем, что речь идет о большом количестве мелких частиц. Точный размер частиц, начиная с которого его называют порошком, не определен. Обычно под высокодисперсными частицами понимают частицы размером не более 100 мкм.
Форма частиц порошка может быть самой разнообразной. В связи с таким разнообразием форм частиц, очень трудно определять размеры частиц. Поэтому введена стандартная характеристика размера частицы – диаметр эквивалентной сферы (ДЭС), т.е. диаметр такой сферы, объем которой равен объему частицы. Средний размер частиц наиболее часто применяемых наполнителей может меняться от нескольких нанометров (ДЭС = 7 нм у аэросила А300, ДЭС = 28 нм у технического углерода П267) до нескольких десятков микрометров (ДЭС = 45 мкм у силикагеля ИКТ-9-7, ДЭС = 120 мкм у мела L1).
Размеры частиц могут быть измерены при помощи ситового анализа – сухого для крупных частиц и мокрого – для частиц, размеры которых меньше 150 мкм. Ситовой анализ дает не ДЭС, а минимальный геометрический размер частиц, проходящих через сито. Например, значения ДЭС для призматических частиц обычно в 1,2÷1,4 раза больше, чем размер, полученный методом ситового анализа. Почти все промышленные минеральные наполнители являются фракционированными, т.е. после прохождения частиц наполнителя через набор сит. Качественный анализ наполнителей обычно заключается в оценке зернистости и характера распределения частиц по размерам.
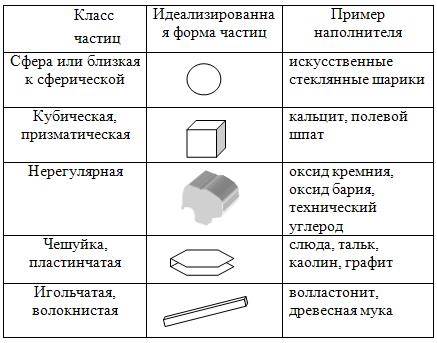
Форма частиц большинства наполнителей различается чрезвычайно сильно (таблица 7.1). Наполнители могут иметь сферические (стеклосферы), кубические (кальцит), призматические (полевой шпат, оксид бария), пластинчатые, чешуйчатые (каолин, слюда, тальк, графит) или игольчатые (силикат кальция, древесная мука) частицы. Кроме этого, многие наполнители имеют настолько сложную форму частиц, что ее невозможно описать любой простой классификацией.
Таблица 7.1 - Формы и основные параметры частиц наполнителя
Одним из важнейших параметров дисперсных наполнителей является удельная поверхность (Sуд). Она определяется как площадь поверхности наполнителя, приходящаяся на единицу массы (измеряется в м2/г или м2/м3). Эффективность введения наполнителей в полимеры во многих случаях зависит от этого параметра.
В зависимости от метода измерения различают геометрическую и адсорбционную удельные поверхности. Геометрическую удельную поверхность (Sгеом) частиц с простой формой (шар, куб, призма) можно рассчитать арифметически. Величина Sгеом наполнителей со сложной формой частиц также определяют расчетным путем, предварительно измерив размеры отдельных участков ее поверхности при помощи микроскопа. Например:
Sгеом = K/ρ ∙ dW/Xm,
где К – коэффициент пропорциональности, учитывающий форму частиц (для сфер К = 6, для призматических частиц К = 12, для пластин К = 18, для тонких частиц К = 18÷30), dW – массовая доля данной фракции, Хm – среднее значение размера частиц (ДЭС) соответствующей фракции.
Из этого следует, что уменьшение размера частиц повышает удельную поверхность наполнителя. Например, для стеклянных сфер с плотностью 2,5 г/см3 и с размером 10 мкм Sгеом = 0,24 м2/г, для сфер с размером 10 нм Sгеом = 240 м2/г.
Однако такой метод определения поверхности частиц сложной геометрической формы не дает точного определения ее размера. Это происходит из-за того, что некоторые наполнители имеют большое количество пор и микропор или других видов несовершенства структуры, которые невозможно измерить при помощи микроскопа. Поэтому для определения удельной поверхности, близкой к истинному значению, определяют адсорбционную удельную поверхность.
Определение удельной адсорбционной поверхности (Sадс) основано на адсорбции поверхностью твердой частицы низкомолекулярных веществ. Принимают, что количество адсорбируемого вещества, необходимое для образования мономолекулярного слоя на частице наполнителя, пропорционально площади ее поверхности:
Sадс = w ∙ am ∙ NА, [м2/г],
где w – площадь, занимаемая одной молекулой низкомолекулярного вещества, am – количество адсорбируемого вещества, необходимое для образования мономолекулярного слоя, NА – число Авогадро.
Для определения количества адсорбата, образующего мономолекулярный слой на поверхности частиц наполнителя, используют теорию полимолекулярной адсорбции БЭТ (Брунауэра, Эммета, Теллера). Для этого экспериментально определяют зависимость количества адсорбированного вещества на исследуемой поверхности от его концентрации (от парциального давления его паров). Экстраполяцией этой кривой к бесконечно малой концентрации сорбата и с использованием теории БЭТ находят емкость адсорбционного монослоя на поверхности наполнителя, и рассчитывают Sадс.
Стандартным является метод низкотемпературной адсорбции азота. Это метод довольно трудоемок. Для его упрощения строят градуировочный график зависимости количества адсорбированного вещества от удельной поверхности порошка при каких-то одинаковых условиях. Для построения такого графика используют порошки с известной Sадс, определенной по вышеописанному методу. Затем, измерив при этих условиях адсорбцию вещества исследуемым порошком, определяют его адсорбционную поверхность по полученному графику. В качестве сорбата используют различные низкомолекулярные вещества, в том числе и красителей. Последние удобны тем, что позволяют легко определять адсорбцию по изменению интенсивности окраски их растворов после внесения в раствор наполнителя.
Значения удельной поверхности для различных наполнителей могут лежать в интервале от 0,3 м2/г (удельная поверхность мела L1) до 1100 м2/г (у канальных саж Sадс = 100÷1100 м2/г, у аэросила А380 Sадс = 380 м2/г)
Максимальна объемная доля наполнителя (φm). Величина φm характеризует максимальное количество наполнителя, которое можно ввести в полимер. Оно определяется как отношение истинного объема частиц наполнителя (Vнп) к общему объему, фактически занимаемому ими (Vобщ) при максимально плотной упаковке частиц:
φm = Vнп / Vобщ .
Максимальное количество наполнителя, которое можно ввести в полимерный материал зависит от формы его частиц и характера их упаковки. Для каждого вида упаковки характерно свое значение φm при их наиболее плотной упаковке.
Таблица 7.2 - Значения φm для различных способов упаковки сфер одинакового размера

В реальных ПКМ частицы всегда упакованы статистически, поэтому величина φm определяется в основном формой частиц. В этих условиях наибольшей величиной φm обладают сферы – 0,64. Любое отклонение формы частиц от сферической снижает φm. Чем более сложная форма частиц, тем меньше φm. Расширение распределения частиц по размерам увеличивает плотность их упаковки и φm благодаря тому, что мелкие частицы распределяются в пространстве между плотно упакованными крупными частицами (бимодальная упаковка). Кроме того, частицы низкотвердых наполнителей могут иметь повышенное значение φm за счет деформирования и разрушения частиц под действием внешних сил при смешении и занятия ими более выгодного пространственного расположения.
Для промышленно применяемых наполнителей φm обычно составляет 0,15÷0,7 (φm каолина К5 = 0,35, φm мела L1 = 0,83). Следует отметить, что величина φm обычно определяется экспериментально. Теоретически φm трудно рассчитать из-за агломерации частиц и отклонения их формы от сферической.
Проще всего величину максимальной объемной доли наполнителей можно определить по масляному числу. Масляное число (М.ч.) – это минимальное количество масла (обычно дибутилфталата – ДБФ), необходимое для полного смачивания 100 граммов наполнителя (измеряется в мл/100 г). Измерение масляного числа происходит следующим образом. В смесительное оборудование помещают 100 г. наполнителя и, измеряя крутящий момент на приводящем валу мешалки, постепенно добавляют масло. В тот момент, когда весь наполнитель будет смочен маслом и все пустоты между частицами наполнителя будут заняты маслом, вязкость системы резко возрастает. Количество масла при этом в миллилитрах и называют масляным числом:
φm = (100/ dнп)/( 100/ dнп+ М.ч.),
где dнп – плотность частиц наполнителя (г/см3).
Коэффициент Эйнштейна (kE). Константа kE характеризует форму частиц наполнителя. Достаточно точным методом определения коэффициента Эйнштейна является реологический метод. Он заключается в построении зависимости эффективной вязкости жидкой среды от объемной доли частиц наполнителя, содержащихся в ней (рис. 7.1).
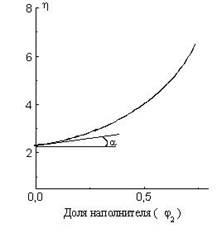
Рис. 7.1 - Зависимость вязкости жидкости от содержания в ней наполнителя.
Тангенс угла наклона начального участка кривой численно равен kE (kE=tgα). Коэффициент Эйнштейна минимален для сфер и равен 2,5. Чем сложнее форма частиц и больше отличается от сферической, тем выше величина kE.
Оба рассмотренных выше параметра – коэффициент Эйнштейна и максимальная объемная доля наполнителя (φm) характеризуют форму частиц наполнителя. Чем сложнее форма частиц наполнителя, тем больше величина kE и меньше значение φm.
Прочность частиц наполнителя очень важна при создании ПКМ. Однако определить это свойство для очень мелких частиц невозможно. Поэтому физико-механические свойства наполнителей оценивают по твердости.
Существуют различные методы оценки твердости материалов, в частности, шкала Мооса, широко используемая для сравнения твердости минералов, которая служит также показателем абразивной способности материалов.
Таблица 7.3 - Показатели твердости материалов по Моосу
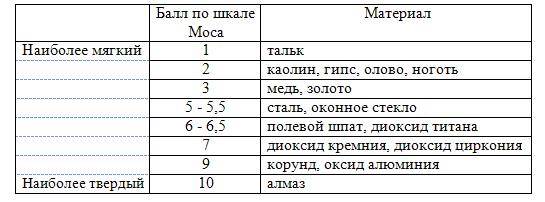
По этому методу дисперсные частицы сравниваются по их способности оставлять царапины на гладкой твердой поверхности эталонных материалов. Шкала Мооса является относительной и нелинейной.
Дата добавления: 2015-06-22; просмотров: 3016;
