Задача 2. Узагальнити закон Ома в диференціальній формі на випадок, коли в системіє ще й градієнт концентрації числа частинок.

Узагальнити закон Ома в диференціальній формі на випадок, коли в системіє ще й градієнт концентрації числа частинок.

Розв 'язок

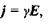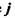Закон Ома в диференціальній формі має вигляд де - густина електричного струму; 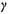- коефіцієнт електро­провідності; 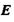- напруженість електричного поля.

Оскільки напруженість зв'язана відомим співвідношен­ням з градієнтом потенціалу електричного поля 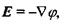то закон Ома набуває такого вигляду:

Згідно з лінійним законом термодинаміки необернених процесів, в присутності градієнта концентрації числа части­нок 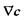маємо таке узагальнення закону Ома в диферен­ціальній формі:

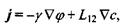
де 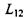- кінетичний коефіцієнт, що відповідає за перехрес­ний процес появи додаткового внеску велектричний струм за рахунок градієнта концентрації числа частинок.

Завдання для перевірки кінцевого рівня знань

1. Записати зміну ентальпії через зміну внутрішньої енергії, об'єму і тиску. Розглянути окремий випадок ізобарної системи.

2. Записати зміну вільної енергії Гіббса через зміну ентальпії, температури і ентропії. Розглянути окремий випадок ізотерміч­ної системи.

3. В об'ємі, що розділений напівпроникною перегородкою, знахо­диться 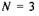молекули. Знайти число мікростанів (термодина­мічну ймовірність) і ймовірність (частоту появи) кожної з конфігурацій.

4. Знайти ентропію кожної з конфігурацій для задачі 3.

5. В об'ємі, що розділений напівпроникною перегородкою, знахо­диться молекули. Знайти число мікростанів (термодина­мічну ймовірність) і ймовірність (частоту появи) кожної з конфігурацій.

6. Знайти ентропію кожної з конфігурацій для задачі 5.

7. В об'ємі, що розділений напівпроникною перегородкою, знахо­диться 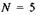молекули. Знайти число мікростанів (термодина­мічну ймовірність) і ймовірність (частоту появи) кожної з конфігурацій.

8. Знайти ентропію кожної з конфігурацій для задачі 7.

9. Написати вираз для потоку частинок при наявності різниці концентрації і температури. Розглянути окремий випадок відсут­ності потоку частинок у такій системі.

10.Написати вираз для потоку частинок при наявності різниці концентрації і тиску. Розглянути окремий випадок відсутності потоку частинок у такій системі.

11.У системі є два градієнти (температури і концентрації) і два потоки (частинок і тепла). Записати відповідні лінійні закони і принцип симетрії кінетичних коефіцієнтів для такої системи.

12.Записати у загальному вигляді лінійний закон для густини електричного струму через мембрану. Взяти до уваги, що з обох сторін мембрани різні концентрації і потенціали електричного поля.