ФРИКЦИОННЫЕ ПЕРЕДАЧИ

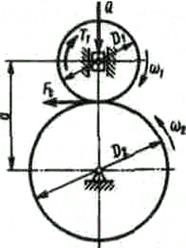
Фрикционной передачей называется механизм, служащий для передачи вращательного движения от одного вала к другому с помощью сил трения, возникающих между насаженными на валы и прижатыми друг к другу цилиндрами (рис. 85, а), конусами (рис. 85, б) или дисками (рис. 85, в, г).

а	б
в	г

Рис. 85

Достоинства фрикционных передач: простота конструкции, бесшумность работы, возможность безаварийной ситуации при случайной перегрузке, возможность плавного изменения передаточного числа на ходу машины. Главный недостаток фрикционных передач – значительная радиальная нагрузка на опоры валов, которая может до 35 раз превышать передаваемое окружное усилие. Кроме того, фрикционные передачи не обеспечивают строгого постоянства передаточного числа при изменении нагрузки и имеют сравнительно невысокий КПД.

Фрикционные передачи находят применение в кузнечно-прессовом оборудовании, металлорежущих станках, транспортирующих машинах; в приборах, счетно-решающих машинах и т.д. Принцип фрикционной передачи является основой технологического процесса в прокатных станах, основой работы рельсового и безрельсового колесного транспорта.

Цилиндрическая фрикционная передача (рис. 85, а) допускает для одной пары катков силовых передач i<7, для передач приборов i<25; окружные скорости катков открытых силовых передач не должны быть больше 10 м/с, а для закрытых передач – 20 м/с. Для закрытых передач КПД h=0,92...0,98, для открытых h=0,8...0,92.

В результате неизбежного при работе фрикционных передач упругого скольжения ведомый каток отстает от ведущего и точное значение передаточного числа будет определяться по формуле

i=w₁/w₂=D₂/[D₁(1–e)],

где e – коэффициент скольжения (для металлических катков e=0,01...0,03, большие значения относятся к передачам, работающим всухую; для текстолитового катка e»0,1). Наличие упругого скольжения и некоторая его зависимость от колебаний нагрузки и условий работы передачи вынуждают называть передаточное число фрикционной передачи условно постоянным. Для практических расчетов силовых фрикционных передач пользуются приближенным значением передаточного числа i»D₂/D₁.

Для передачи от одного вала к другому крутящего момента необходимо за счет силы трения приложить к ведомому катку окружную силу

F_t=2T₁/D₁,

которая должна быть меньше наибольшей силы трения покоя, возникающей между катками, прижатыми друг к другу силой Q. Таким образом, условие работы фрикционной передачи записывается так:

kF_t=F_mp=fQ,

где k – коэффициент запаса сцепления (k=1,3...1,4); f – коэффициент трения (для стальных или чугунных катков, работающих в масляной ванне f=0,04...0,05; работающих всухую f=0,15...0,20; для передач с одним неметаллическим катком f=0,2...0,3).

Из вышеприведенной формулы определим силу прижатия катков:

Q=kF_t/f=2kT/(fD).

Из этой формулы видно, что сила прижатия катков больше окружной силы в k/f раз, что при k=1,4, f=0,04 дает k/f=1,4/0,04=35 раз. Большие силы прижатия катков создают значительные радиальные нагрузки на опоры валов и вызывают появление больших контактных напряжений на рабочих поверхностях катков, что делает силовые фрикционные передачи громоздкими, а их нагрузочную способность сравнительно невысокой.

Для уменьшения в несколько раз силы прижатия применяют катки с клинчатым ободом (рис. 86, б). Однако в таких катках возникает значительное геометрическое скольжение, существенно уменьшающее срок их службы.

Для катков, изготовленных из материалов, подчиняющихся закону Гука (металлы и текстолит), наибольшие контактные напряжения s_H вычисляются по формуле Герца:

,

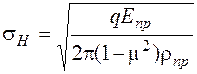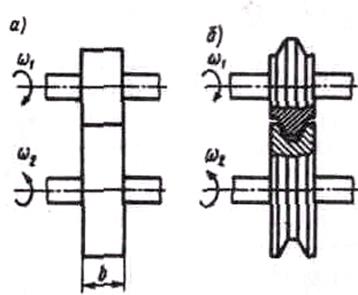Рис. 86

где q=Q/b – номинальная нагрузка на единицу длины контактной линии, b – ширина катков; Еnp= =2E1E2/(E1+Е2) – приведен-ный модуль упругости материалов катков; rnp= =0,5D1D2/(D1+D2) – приве-денный радиус кривизны катков; m – коэффициент Пуассона материала катков.

Основным расчетным параметром цилиндрической фрикционной передачи будем считать межосевое расстояние а, а условие износостойкости запишется в виде неравенства

s_H<[s_H],

где [s_H] – допускаемое контактное напряжение для катка из менее прочного материала.

Вышеприведенное условие износостойкости катков используется для проверочного расчета имеющейся передачи. Формулу для проектного расчета передач с металлическими и текстолитовыми катками получим из формулы Герца, приняв коэффициент Пуассона m=0,3, выразив диаметры катков через межосевое расстояние а и передаточное число i; силу прижатия Q выразим через крутящий момент Т₁, а ширину катка примем b=y_aa, где y_a=0,2...0,4 – коэффициент ширины катка по межосевому расстоянию, тогда

,

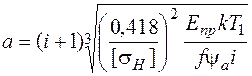где k – коэффициент запаса сцепления; f – коэффициент трения.

Вычислив межосевое расстояние, определяем размеры катков по формулам:

D₁=2a/(i+1), D₂=D₁i, b=y_aa,

причем должно соблюдаться условие b£D₁, а ширину обода малого катка принимают на 2...5мм больше расчетной, так как возможно осевое смещение катков из-за неточностей изготовления и сборки.

Допускаемые контактные напряжения устанавливают в зависимости от материалов катков, твердости НВ рабочих поверхностей или предела прочности при изгибе s_ви и условий работы передачи. Ориентировочно для стальных катков, работающих всухую, [s_H]=1,2...1,5 НВ, МПа; для стальных катков, работающих в масляной ванне, [s_H]=2,4...2,8 НВ, МПа; для чугунных катков [s_H]»l,5s_ви; для текстолитовых катков [s_H]=80...100 МПа.

Расчет неметаллических катков, материал которых не подчиняется закону Гука, ведут понагрузке q на единицу длины контактной линии по условию

q=Q/b£[q],

где Q – сила прижатия катков; b – ширина катков; [q] – допускаемая удельная нагрузка; для пластмасс ориентировочно [q]=40...80 Н/мм, для дерева [q]=2,5...5 Н/мм, для резины [q]=10...30 Н/мм, для кожи [q]=15...25 Н/мм.

Так как Q=2kT₁/(fD₁), a D₁=2a/(i+1), то, приняв q=[q], получим формулу для проектного расчета передач с неметаллическими катками

.

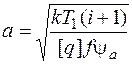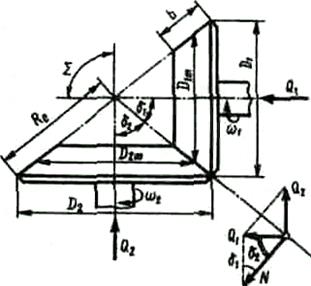
Коническиефрикционные передачи (рис. 85, б) преобразовывают вращательное движение между валами, оси которых пересекаются, причем обычно угол между осями S=d₁+d₂=90°, где d₁ и d₂ – половины углов при вершине конусов ведущего и ведомого катков. В конических передачах скольжение теоретически отсутствует.

Основными геометрическими параметрами передачи являются (рис. 85, б): конусное расстояние 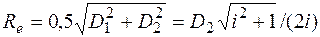, где D₁ и D₂ – диаметры катков.

Для передачи крутящего момента необходимо катки прижать друг к другу, создав силу нормального давления N и обеспечив условие

kF_t=F_mp=fN,

где k – коэффициент запаса сцепления; F_t=2T₁/D_1m – окружная сила; f – коэффициент трения. Для определения силы Q₁ прижатия катков разложим эту силу по реальным направлениям на составляющие N и Q₂ (рис. 85, б), тогда

Q₁=Nsind₁, Q₂=Nsind₂.

Из этих равенств видно, что для обеспечения одной и той же силы нормального давления N надо к ведущему катку приложить силу Q₁ или к ведомому – силу Q₂, причем Q₁<Q₂, если d₁<d₂. Отсюда следует, что выгодно нажимным делать меньший каток.

У ортогональных передач (S=90°), для которых D₂/D₁=tgd₂, передаточное число можно также определить по формуле i=tgd₂=ctgd₁. Для конических фрикционных передач рекомендуется i<4, а их КПД h=0,85...0,9.Критерий работоспособности и принципы расчета конических фрикционных передач аналогичны рассмотренным ранее для цилиндрических передач, но основным расчетным параметром следует считать средний диаметр D_m большего (обычно ведомого) катка, так как в основном именно этот размер определяет габариты передачи.

На рис. 87 представлена схема реверсивной конической фрикцион-ной передачи винтового пресса, в которой ведущие катки 1 поочередно сцепляются с ведомым катком 2,причем ведомый вал меняет направление вращения, а винт получает рабочий и обратный ход. Обычно катки такой передачи делают из чугуна, а обод ведомого шкива покрывают кожаной лентой, прорезиненной тканью или прессованным асбестом; иногда обод ведомого катка изготовляют из пластмассы.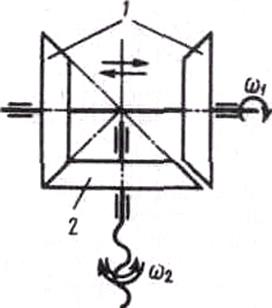

Рис. 87

Вариатором или бесступенчатой передачей называется механизм для плавного изменения передаточного отношения. В машиностроении фрикционные вариаторы используют в силовых приводах, мощность которых колеблется от небольших величин до десятков и даже сотен киловатт. Вариаторы бывают одно- и двухступенчатые.

Основной кинематической характеристикой любого вариатора является диапазон регулирования Д, равный максимальному передаточному отношению, деленному на минимальное

Д=i_max/i_min.

Для одноступенчатых вариаторов преимущественные значения Д=3...6. С увеличением диапазона регулирования снижается КПД вариатора.

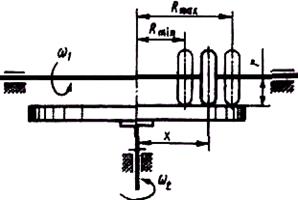
На рис. 85, в изображена схема лобового вариатора, в котором оси взаимно перпендикулярны, а изменение скорости ведомого вала происходит за счет осевого перемещения ролика. Лобовой вариатор допускает реверсивные вращения ведомого вала при одностороннем вращении ведущего. Ведущим звеном в лобовой передаче может быть либо ролик, либо работающий торцом диск. Передаточное число лобового вариатора

i=w₁/w₂=x/r,

а диапазон регулирования

Д=i_max/i_min=R_max/R_min.

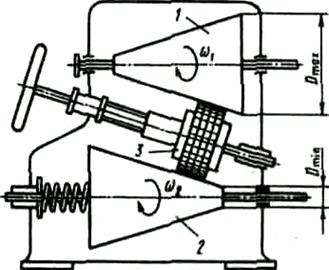
На рис. 85, г представлена схема двухконусного вариатора с параллельными осями. Изменение передаточного отношения происходит за счет перемещения с помощью винтового механизма промежуточного цилиндрического катка 3, зажатого между рабочими поверхностями конических катков 1 и 2.

Так как i_max=D_max/D_min, а i_min=D_min/D_max, то диапазон регулирования Д=i_max/i_min= .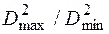

Материалы тел качения фрикционных передач должны обладать высокой износостойкостью и прочностью рабочих поверхностей, возможно большим коэффициентом трения скольжения, высоким модулем упругости (для уменьшения упругого скольжения). Максимальную нагрузочную способность имеют катки из закаленной стали типа ШХ15, которые могут работать в масляной ванне и всухую. Применяются в силовых передачах также чугунные катки и сочетания текстолитовых и стальных или чугунных катков. Кроме того, для изготовления катков или их облицовки (для повышения коэффициента трения) применяют кожу, резину, прорезиненную ткань, дерево, фибру и другие материалы. Катки из неметаллических материалов работают всухую.

При разных материалах тел качения ведущий каток делают из менее прочного материала во избежание повреждения катков в случае буксования передачи.