Характеристики дифференцирующей цепи и линии задержки.

Дифференцирующая цепь

Схема дифференцирующей цепи приведена на рис.22.

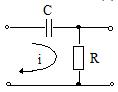
Рис.22 Схема дифференцирующей цепи

Изображение по Лапласу напряжений на элементах схемы 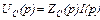, тогда с учетом (4.4) получим:

, .

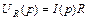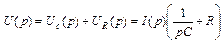По определению .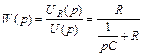

Умножив числитель и знаменатель на рС, получим: 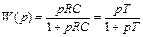, где T = RC - постоянная времени RC-цепи.

Этой передаточной функции соответствует дифференциальное уравнение, следующее из соотношения: 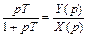, откуда .

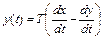Здесь .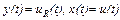

Основные характеристики дифференцирующей цепи:

ККП: ; ; ;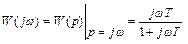

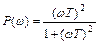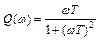АЧХ: ;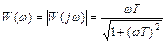

ЛАЧХ: ;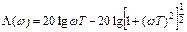

ФЧХ: ;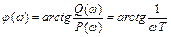

ПХ: ;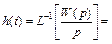

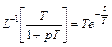ИХ: = .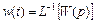

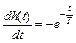На рис.23 приведены годограф ККП, ЛАЧХ, ЛФЧХ, ПХ и ИХ дифференцирующей цепи, а также кусочно-линейная аппроксимация ЛАЧХ.

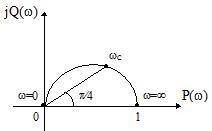
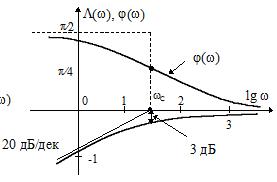
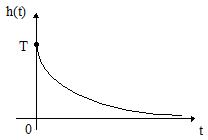
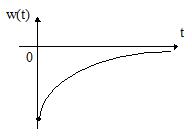
Рис.23 График годографа ККП, ЛАЧХ, ЛФЧХ, ПХ и ИХ дифференцирующей цепи

Линия задержки

Звено называется минимально-фазовым, если все нули и полюсы его передаточной функции имеют отрицательные или равные нулю вещественные (действительные) части.

Звено называется неминимально-фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.

Примером неминимально-фазового звена является линия задержки или звено запаздывания. Сигнал на выходе линии задержки связан с входным сигналом соотношением:

,

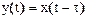где 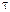- время задержки, откуда

.

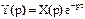По определению .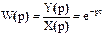

Полюсов эта функция не имеет, а единственный нуль определяется из уравнения 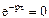, откуда .

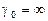Основные характеристики линии задержки:

ККП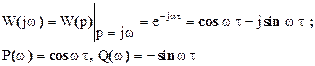

АЧХ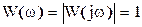

ЛАЧХ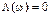

ФЧХ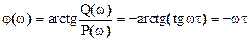

ПХ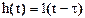

ИХ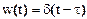

Из этих выражений видно, что АЧХ линии задержки не зависит от частоты, а ФЧХ линейна с отрицательным наклоном, пропорциональным времени задержки t.