Методы описания и представления синусоидального тока, ЭДС и напряжения
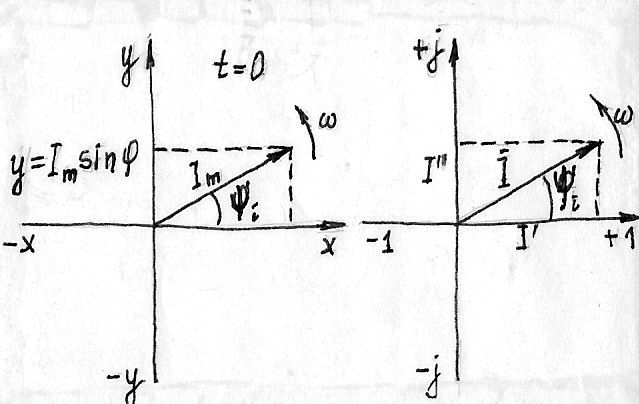 Представление синусоидального тока в виде вращающегося вектора:
Представление синусоидального тока в виде вращающегося вектора:
а) декартова плоскость;
б)комплексная плоскость.
Синусоидальные токи, ЭДС и напряжения можно описать с помощью тригонометрических функций, изобразить графически в виде временной диаграммы синусоиды и представить в виде вращающихся векторов на декартовой и комплексной плоскостях.
Как известно, синусоидальный ток может быть описан тригонометрической функцией:
i=Imsin(ωt+Ψ)
При представлении синусоидальных величин в виде вращающихся векторов на плоскости декартовых координат:
· Вектор, соответствующий в выбранном масштабе амплитудному значению синусоидальной величины (Em, um, Im), вращается с угловой частотой, равной угловой частоте ω против часовой стрелки;
· Начальная фаза отсчитывается от положительного направления оси абсцисс также против часовой стрелки;
· Проекции вращающихся векторов на ось ординат равны мгновенным значениям синусоидальных величин.
Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, называются векторной диаграммой.
Применение векторных диаграмм при анализе и исследовании цепей переменного тока позволяет наглядно представить рассматриваемые процессы, а также рассчитать цепь.
При этом для получения суммы или разности ЭДС, u, I используются правила сложения или вычитания векторов.
Недостатком таких расчетов является невысокая точность.
При представлении синусоидальных ЭДС, u, I в виде аналогичных вращающихся векторов, на комплексной плоскости позволяет выразить геометрические операции с векторами переменных токов и напряжений в алгебраической форме, что повышает точность расчётов и обеспечивает возможность применения для расчёта цепей синусоидального тока.
При изображении синусоидальных величин в виде вращающихся векторов на комплексной плоскости ось абсцисс заменяют осью действительных (вещественных) чисел, а ось ординат - осью мнимых чисел;
· Вращающийся вектор, соответствующий в выбранном масштабе действующему значению синусоидальной величины, изображают аналогично тому, как это производилось на плоскости декартовых координат;
· Вектор, обозначенный I, раскладывают на составляющие по оси действительных I` и оси мнимых I`` чисел;
·  Составляющую по мнимой оси выделяют множителем j
Составляющую по мнимой оси выделяют множителем j
j= - мнимая единица.
[В отличие от принятого в математике обозначения мнимой единицы через i в электротехнике применяют обозначение j , чтобы различать с обозначением мгновенного значения тока i ].
Алгебраическая форма записи:
i=I`+jI`` - комплекс тока.
Показательная форма записи:
i=IejΨ
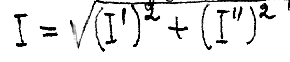 где I=> модуль комплекса тока.
где I=> модуль комплекса тока.
Ψ=> фаза комплекса тока
Ψ=arctg I``/I`
Тригонометрическая форма записи получается преобразованием показательной формы на основании формулы Эйлера:
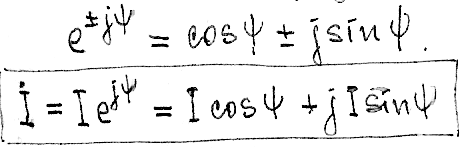
Кроме того, будут использоваться следствия из формулы Эйлера:
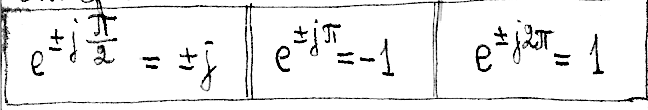
1.2.5 Закон Ома в комплексной форме для цепи с резистивным элементом.
| i |
| ur |
| uR |
| r |
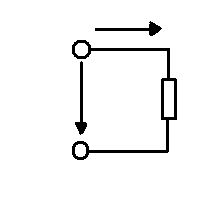
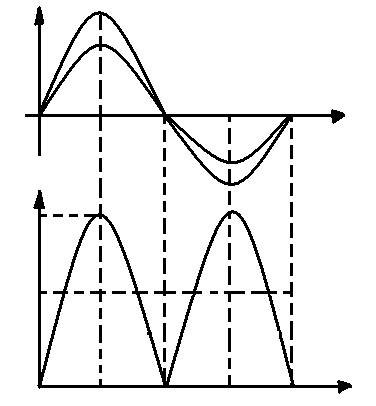
Рис.1.49. Цепь синусоидального тока с резистивным элементом: а) схема; б) временные графики мгновенных значений Ur, i, Pr .
Пусть на вход цепи с активным сопротивлением (резистивным элементом ) рис.1.49, а подано напряжение синусоидальной формы
UR = URM sin (ωt+ψU)
Необходимо установить, как изменяются ток і в цепи и мощность PR, выделяемая на сопротивления r. Согласно закону Ома для мгновенных значений u и i
I = UR/r = URM/r sin (ωt+ψU ) = IM sin (ωt+ψI)
где IM = URM/r - амплитуда тока. Для действующих значений I = UR/r
ψU = ψI = ψ т.е формы u и i совпадают.
Мгновенные значения мощности
PR=UR i=i2r
знака не из меняют, т.е всегда положительный.
Пусть ψ=0, тогда (см. рис 1.49.в)
PR = UR I = URM IM sin2ωt = URM IM ½ (1-cos2 ωt) =
= URM / 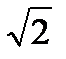 * IM /
* IM / 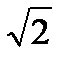 (1- cos2 ωt) = UR I - UR I cos2 ωt
(1- cos2 ωt) = UR I - UR I cos2 ωt
PR.MAX = 2URI
PR.CP=1/T 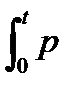 R dt = 1/T
R dt = 1/T 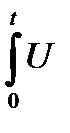 R I dt – 1/T
R I dt – 1/T 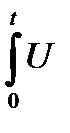 R I cos2 ωt dt =
R I cos2 ωt dt =
UR I - UR I / T sin (4 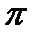 /T)t |t0
/T)t |t0  = UR I = I2 r
= UR I = I2 r
т.е средняя мощность равна произведению действующих значений напряжений u тока.
Изобразим рассматриваемые синусоидальные величины на комплексной плоскости, полагая ψU=ψI=ψ и t=0 (рис.1.50)
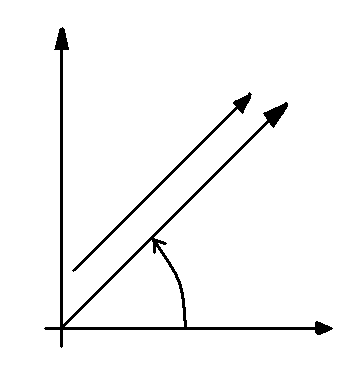 Рис.1.50 векторная диаграмма
Рис.1.50 векторная диаграмма
для цепи синусоидального тока
с резистивным элементом.
Напряжения ÙR = UR e jψ; ток İ = ŮR/r = UR/r e jψ = I e jψ ;
выражения İ = ŮR/r
представляет собой запись закона Ома в комплексной форме для цепи с резистивным элементом.
1.2.6. Закон Ома в комплексной форме для цепи с идеальной катушкой индуктивности.
Предположим, что в цепи с катушкой индуктивности активное сопротивление катушки rL=0 и активное сопротивление подводящих проводов rпр = 0. Такой случай является идеальным (рис.1.51а).
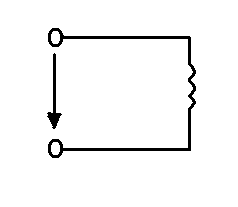
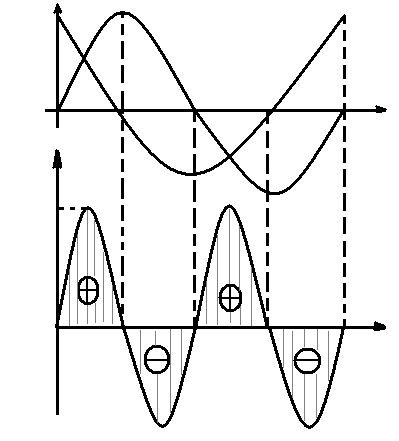
Рис. 1.51 Цепь синусоидального тока с идеальной катушкой индуктивности: а) схема; б) временные графики мгновения значений uL , i, pL.
Пусть в этой цепи протекает синусоидальный ток
I = IM sin (ωt+ψi)
тогда мгновенное напряжение катушке
uL = -eL = L di/dt = ω L IM cos (ωt+ψi) = ULM sin (ωt+ψi + 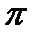 /2) (1.11)
/2) (1.11)
где ULM = ω L IM
Из (1.11) следует, что синусоида напряжения на идеальной катушке индуктивности опережает по фазе синусоида тока на угол сдвига фаз 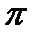 /2. (рис. 1.51б).
/2. (рис. 1.51б).
Изобразим рассматриваемые синусоидальные величины на комплексной плоскости, перейдя к действующим значениям (рис. 1.52):
Рис. 1.52 векторная диаграмма для цепи sin тока с идеальной катушкой индуктивности
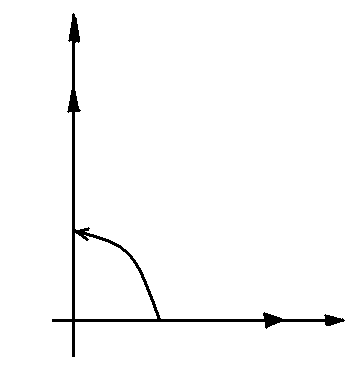
Ì = I e jψi ;
ÙL = UL e j (ψi+ 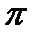 /2) = ω L I e jψi e j
/2) = ω L I e jψi e j 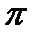 /2 = jω L I e jψi = j ω L Ì = j xL Ì , (1.12)
/2 = jω L I e jψi = j ω L Ì = j xL Ì , (1.12)
где xL = ωL -модуль активного сопротивления катушки [ c-1Oм*c = Oм]
j xL – комплекс индуктивного сопротивления.
На основании выражения (1.12) ранее сформулированное правило о фазовом соотношении тока и напряжения в цепи с идеальной катушкой индуктивности сводится к следующему:
-вектор напряжения на идеальной катушке индуктивности опережает по фазе вектор тока на угол сдвига фаз π/2.
Закон Ома в комплексной форме имеет вид
Ì = ÙL / j xL или для модулей: I = UL / xL.
Мгновенное значения при ψI = 0
pL =uL I = ULM IM sin (ωt+ 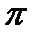 /2) sin ωt =
/2) sin ωt =
= ULM IM 1/2 [ cos 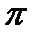 /2 –cos(2ωt +
/2 –cos(2ωt + 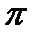 /2) ] =
/2) ] =
= - UL I cos (2ωt + 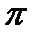 /2) = xL I2 sin ωt
/2) = xL I2 sin ωt
Следовательно, мгновенная мощность имеет амплитудное значениe xL I2 и изменяется с данной частотой 2ω (рис.1.51.б)
В первую четверть периода uL > 0 , I > 0, pL> 0, энергия источника переходит в энергию магнитного поля катушки индуктивности. Максимальное значение накопленной энергии
WL = ½ L I2m
Во вторую четверть периода uL < 0 , I > 0, pL  < 0, энергия магнитного поля катушки возвращается и источник. Cредняя мощность за период
< 0, энергия магнитного поля катушки возвращается и источник. Cредняя мощность за период
PL.CP = 1/T 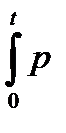 L dt = 0
L dt = 0
Таким образом, в цепи с идеальной катушкой индуктивности непрерывное колебание (обмен) энергия между источником и магнитным полем катушки без затрат энергии источника.
Амплитуда колебаний мощности в цепи с идеальной катушкой называется реактивной индуктивной мощностью;
эта мощность, обусловлена энергией магнитного поля индуктивности;
единица измерения – вар – вольт - ампер - реактивности.
QL = ULI = XLI2
1.2.7 Закон Ома в комплексной форме для цепи с идеальным конденсатором.
Идеальный конденсатор не имеет активных потерь. Предположим, что активное сопротивление конденсатора rS= 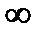 , а активное сопротивление подводящих проводов rпр=0.
, а активное сопротивление подводящих проводов rпр=0.
Цепь с идеальным конденсатором показана на рис. 1.53.а
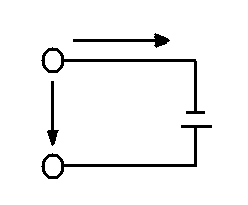

Рис. 1.53 Цепь синусоидального тока с идеальным контуром: а) схема; б) временные графики мгновенных значений uC, i, pC .
Пусть в этой цепи действует синусоидальное напряжение
uC =UCM sin (ωt+ψu)
Тогда мгновенным значением тока
I =C (duC/dt) = ω CUCM cos (ωt+ψu) = IM sin (ωt+ψu+ 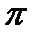 /2) (1.13)
/2) (1.13)
Где IM = ω CUCM = UCM / (1/ω C)
Из (1.13) следует, что синусоида емкостного тока опережает по фазе синусоиду напряжения на кондукторе на угол сдвига фаз π/2 (рис. 1.53.а ).
Изобразим рассматриваемые sin величины на комплексной плоскости, перейдя к действующим значением (рис. 1.54)
Рис. 1.54 векторная диаграмма sin тока 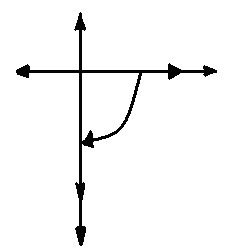
для цепи sin тока с идеальным конденсатором.
ÙC = UC e jψu
Ì = I e j(ψu+ 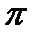 /2) = UC / (1/ω C) e jψu e j
/2) = UC / (1/ω C) e jψu e j 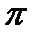 /2 =
/2 =
= j UC / xC e jψu = ÙC / -jxC
Для модулей : I = UC / xC
Где xC = 1/ ω C - модуль емкостного сопротивления конденсатора.
Выражения (1.14) представляет собой запись закона Ома в комплексной форме для цепи с идеальным конденсатором. На основании данного выражения ранее сформулированное правило о фазовом соотношении тока и напряжения в цепи с идеальным конденсатором сводится к следующему: -вектор тока в цепи с идеальным конденсатором опережает по фазе вектор напряжения на углом сдвига фаз π/2 . Mгновенное значение мощности при ψU = 0
pC = uC I = UCM IM sin ωt sin (ωt+ 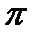 /2) = UCM IM ½ [ cos π/2 – cos(2 ωt+
/2) = UCM IM ½ [ cos π/2 – cos(2 ωt+ 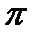 /2) ] = - UC I cos (2ωt+
/2) ] = - UC I cos (2ωt+ 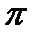 /2) = UC I sin 2ωt = xC I2 sin 2ωt .
/2) = UC I sin 2ωt = xC I2 sin 2ωt .
Следовательно, мгновенная мощность имеет амплитудное значения xC I2 и изменяется с двойной частотой 2ω (рис.1.53 а).
В первую четверть периода uL > 0 , I > 0, pL> 0, энергия источника переходит в энергию электрического поля конденсатора (конденсатор разряжается )! Max значение накопленной энергии WC = ½ CU2CM . Во вторую четверть периода nC > 0, I < 0, pC < 0 , энергия электрического поля возвращается в источник (конденсатор разряжается )!
Средняя мощность за период PС.CP = 1/T 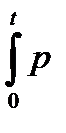 L dt = 0. Таким образом, в цепи с идеальным конденсатором происходит непрерывное колебание (обмен) энергии между источником и электрическим полем конденсатора без затрат энергии источника. Амплитуда колебаний в цепи с идеальным конденсатором называется реактивной емкостью (мощность, обусловленная энергией электрического поля емкости )
L dt = 0. Таким образом, в цепи с идеальным конденсатором происходит непрерывное колебание (обмен) энергии между источником и электрическим полем конденсатора без затрат энергии источника. Амплитуда колебаний в цепи с идеальным конденсатором называется реактивной емкостью (мощность, обусловленная энергией электрического поля емкости )
QС= UС I= XСI2
1.2.8 Законы Кирхгофа в комплексной форме для цепей синусоидального тока
Законы Кирхгофа как универсальные законы электрических цепей в цепях переменного тока справедлива для мгновенных значений ЭДС, токов и напряжений. Для цепей sin тока во многих случаях целесообразнее уравнения электрического состояния цепей по законам Кирхгофа записывають в векторной форме.
Первый закон Кирхгофа для цепей sin тока записывается и формулируется так
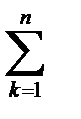 ÌK = 0
ÌK = 0
т.е геометрическая сумма векторов тока ветвей сходящихся в узле, равна нулю.
Узел цепи, в котором сходится токи Ì1, Ì2, Ì3 показана на рис. 1.55а, а векторная диаграмма на комплексной плоскости для токов этого узла на рис 1.55,б
Рис. 1.55 к пояснению I Закона Кирхгофа в комплексной форме а) узел эл. цепи б) векторная диаграмма токов данного узла на комплексной форме
Уравнение по I закону Кирхгофа для этого узла имеет вид Ì1 - Ì2 - Ì3 = 0 или
Ì1 = Ì2 + Ì3 т.е. вектор тока Ì1 равен векторной (геометрической) сумме векторов токов Ì2 и Ì3 (рис.1.55.б)
При представлении sin токов комплексными величинами I закона Кирхгофа формулируется так: алгебраическая сумма значений токов , сходящихся в узле , равно нулю.
Bторой закон Кирхгофа записывается и формулируется следующим образом:
-для замкнутого контура геометрическая сумма векторов эдс , действующих в контуре, равна геометрической сумме векторов напряжений его участков.
B комплексной форме :
-для замкнутого контура алгебраическая сумма комплексов эдс равна алгебраической сумме комплексов напряжений.
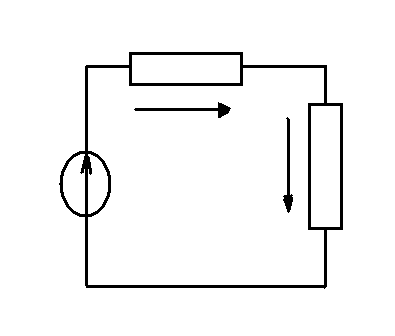
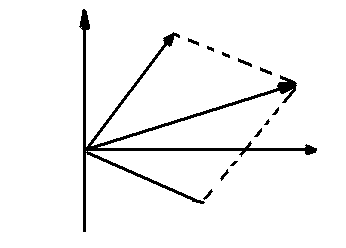
Рис.1.56 к пояснению второго закона Кирхгофа в комплексной форме: а) замкнутый контур электрической цепи; б) векторная диаграмма ЭДС и напряжений данного контура на комплексной плоскости. Уравнение по второму закону Кирхгофа для данной цепи (рис. 1.56.а) имеет вид (рис. 1.56б)
Лекция №6
1.2.9 Цепь синусоидального тока с реальной катушкой индуктивности
Рис 1.57 цепь sin тока с реальной катушкой
индуктивности
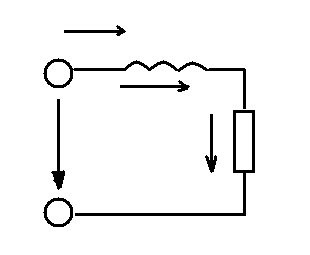
В реальной цепи активное сопротивление катушки и проводов учтено резистором r ( рис. 1.57)
Пусть ток в цепи изменяется по sin закону
I = IM sin (ωt+ψi)
Согласно второму закону Кирхгофа для мгновенных значений напряжения
U = UL + UR
Переходя к комплексам напряжений, получаем:
Ù = ÙR + ÙL = r Ì + j xL Ì =Ì (r + jx) = Ì Ż
Где Ż- r + jx комплекс полного сопротивления цепи Z= 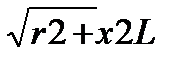 - его модуль
- его модуль
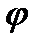 L = arctg xL/r - его фаза; Ż = Z ej
L = arctg xL/r - его фаза; Ż = Z ej 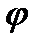 L показательная форма записи полного сопротивления.
L показательная форма записи полного сопротивления.
По закону Ома в комплексной форме Ì = Ù / Ż, или для модулей I = U / Z
Получаем где Ù = Ì Ż = I e jψi Z ej 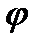 L =U e jψu, ψU = ψI + φL ; φL = ψU - ψI
L =U e jψu, ψU = ψI + φL ; φL = ψU - ψI
Переходя к мгновенным значениям u =UM sin (ω t+ ψi + φL)
Следовательно в цепи содержащей последовательное соединение L и r, синусоида напряжения на входе в цепи (т.е суммарного напряжения) опережает по фазе синусоиду тока на угол сдвига тока на угол сдвига фаз φL (комплекс суммарного напряжения опережает тока на угол сдвига фаз φL )
(рис. 1.58)
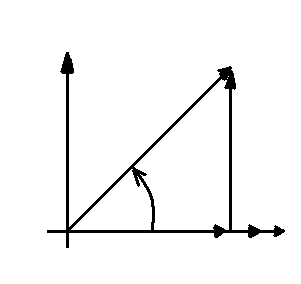
Рис. 1.58 векторная диаграмма с реальной катушкой индуктивности.
Векторная диаграмма строится следующим образом: по оси 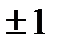 в выбранных масштабах откладывают вектор тока Ì (по условию ψi=0) совпадающий с ним по фазе вектор напряжения на резисторе r: ÙR =r Ì
в выбранных масштабах откладывают вектор тока Ì (по условию ψi=0) совпадающий с ним по фазе вектор напряжения на резисторе r: ÙR =r Ì
Из конца вектора ÙR параллельно оси 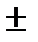 j вверх в том же масштабе, что и ÙR откладывают вектор напряжения на индуктивном элементе L: ÙR = j xL Ì
j вверх в том же масштабе, что и ÙR откладывают вектор напряжения на индуктивном элементе L: ÙR = j xL Ì
Из начало координат под углом φL откладывают отрезок, равный модулю суммарного напряжения Ù = Ì Ż т.е строят вектор напряжения Ù.
Его конец должен совпадать с концом вектора ÙL т.к по 2 закону Кирхгофа Ù = ÙR + ÙL
При выполнения условия совпадения конца вектора суммарного напряжения с концом последнего вектора напряжения участка цепи говорят, что многоугольник напряжений, действующих в цепи, замкнут
Tg φL = xL/r или cos φL = r/z
мгновенная мощность при ψi=0 (рис. 1.59)
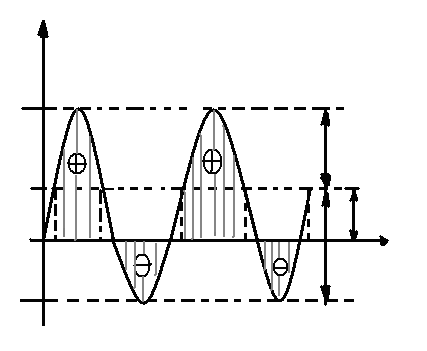
Рис 1.59 график изменения мгновенной мощности в цепи реальной катушкой индуктивности.
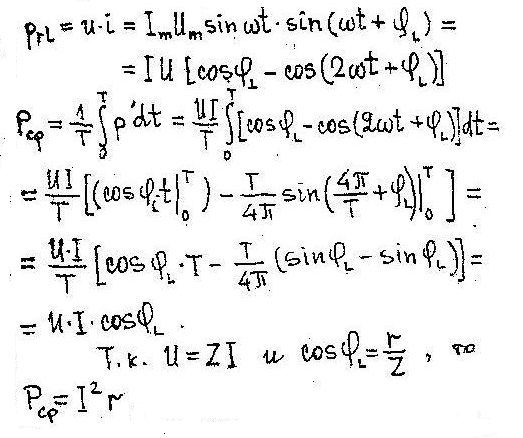
т.е среднее значение мощности в цепи с реальной катушкой индуктивности равно активной мощности ( выделяемой на резисторе r) .
Амплитуда колебания мощности относительно Рср называется полной мощностью цепи, В*А (это наибольшее значениe активной мощности которое может быть получено при данных значениях напряжения и тока):
S = U I [B A]
Pеактивная индуктивная мощность катушки.
QL = XL I2 = UL I
Из векторной диаграммы (рис. 1.58) следует:
Ur = U cosφL
UL=U sinφL
поэтому:
QL= UL I = U I cosφL = S cosφL
P = S cosφL
P = URI = U I cosφL = S cosφL
P2 + Q2 = (U I cosφL)2 + (U I sinφL)2 = (U I)2 = S2
S = 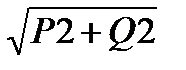
Еще раз подчеркнем что мощность Р является средней мощностью преобразования электроэнергии в другие виды энергии, а реактивная мощность Q характеризует амплитуду колебаний мощности при обмене энергии между источником и магнитным полем катушки.
Введем понятие коэффициента мощности cosφL = P / S.
Который характеризует соотношение между активной и реактивной (в данном случае – индуктивной ) мощностями, т.е показывает, какую часть полной мощности цепи составляет активная мощность. Представим активную и полную мощности в комплексной форме:
Ŝ = P + jQL = S cosφL + jS sinφL
Перейдем к показательной форме на основании подстановки Эйлера:
Ŝ = S e jφL Ŝ = U I e j (ψu -ψ I) = U e j ψu I e -j ψ I = U I
Следовательно для получение полной мощности в комплексной форме необходимо комплекс напряжения умножить на сопряженный комплекс тока:
Ŝ = U I = U e j ψu I e -j ψ I = S e jφL = P+ j Q
Лекция №7
1.3. Резонанс в цепях sin тока. Колебательный контур.
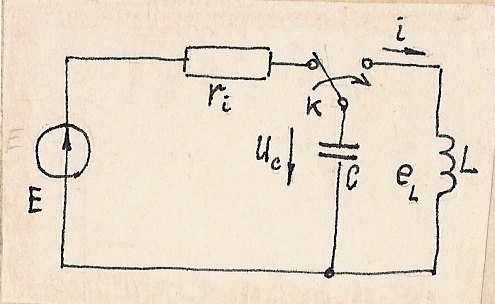
Рис1.68. К возникновению колебаний в идеальном LC-контуре
Предположим, конденсатор С (рис.1.58), подключенный через ключ К к источнику Е, зарядился до напряжения U(l)>0. Энергия запасенного в нем электрического поля: 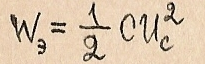
При переключении ключа К к заряженному конденсатору С подключается катушка индуктивности L и образуется замкнутый контур.
Ток в контуре нарастает постепенно, т.к. его увеличению противодействует ЭДС самоиндукции : 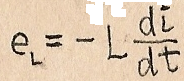
По мере возрастания тока в катушке запасается энергия магнитного поля :
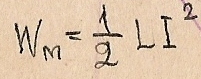
Когда конденсатор разрядится , ток в контуре поддерживает ЭДС самоиндукции до момента, пока энергия запасенного магнитного поля катушки не уменьшится до нуля.
Этот ток заряжает емкость до U(c)<0. описанный процесс повторяется. Замкнутый контур с элементами L и C называется Колебательным.
В идеальном колебательном контуре отсутствуют активные потери, поэтому в нем происходят незатухающие колебания.
В реальном контуре есть активные потери и поэтому возникающие колебания постепенно затухают.
При подключении колебательного контура к источнику гармония. ЭДС в нем при определенных условиях возникают резонансные явления.
Возможны два вида резонанса: при последовательном соединении элементов контура и источника – резонанс напряжений; при параллельном соединении элементов контура и источника – резонанс токов.
1.3.1. Последовательный колебательный контур. Резонанас напряжений.
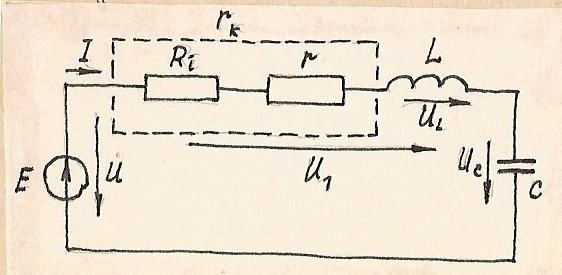
Рис.1.69. Последовательный колебательный контур.
Заменим последовательное соединенные сопротивления R(i) + r сопротивлением r(k)=R(i)+r.
Тогда комплекс полного сопротивления этой цепи:
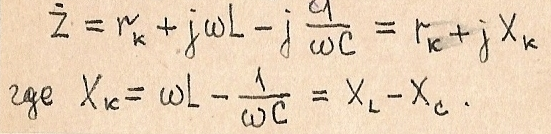
Рис.1.70. Зависимость реактивных сопротивлений от частоты
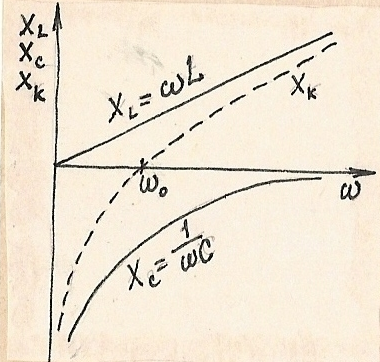
На частоте 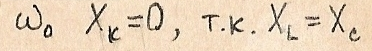
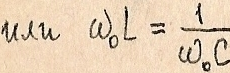
Частота резонанса: 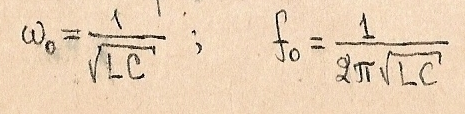
Характеристическое сопротивление контура: 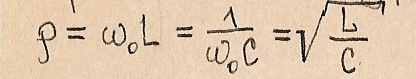
Добротность контура: 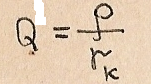
Чем меньше активное сопротивление контура r(k), тем выше его добротность.
С другой стороны : 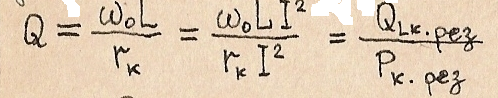
Добротность равна отношению (при резонансе) реактивной мощности в контуре (Q(lk)рез или Q(ck)рез) к активной мощности, поглощаемой контуром.
Полное сопротивление контура при резонансе Z=r(k), т.е. оно становится минимальным и чисто активным:
При этом ток в контуре при резонансе: 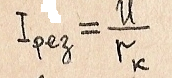
Не зависит от величин Х(l) и X(c), и если Р>r(k), то при резонансе ток в контуре резко возрастает.
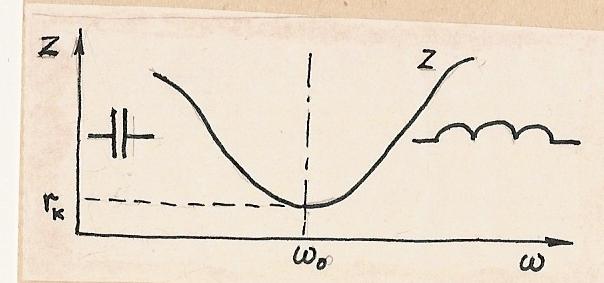
Рис.1.71. Зависимость модуля полного сопротивления последовательного контура опт частоты .
На частоте резонанса:  -
- 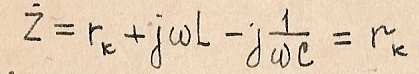
При 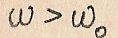 реактивное сопротивление контура носит индуктивный характер, а при -емкостной.
реактивное сопротивление контура носит индуктивный характер, а при -емкостной.
При резонансе в последовательном контуре напряжение на реактивных элементах U(l),U(c) в Q раз превышают напряжение источника U, поэтому резонанс в этом контуре называется резонансом напряжений:
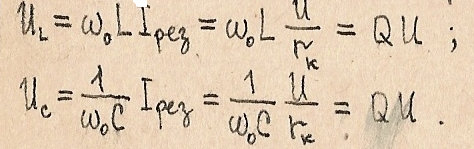
Физически это объясняется колебаниями реактивной энергии в контуре от L к C и обратно. Обмен энергией между источником и контуром не происходит. Ток в цепи обусловлен только активной мощностью.
Представим ток в контуре в колебательной форме:
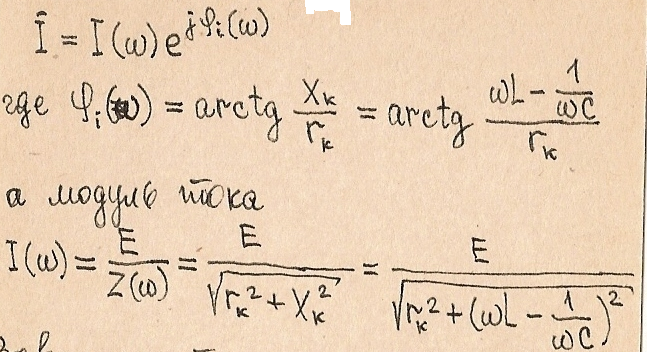
Зависимость модуля тока от частоты при постоянных L,C,r,E называется резонансной характеристикой (резонансной кривой).
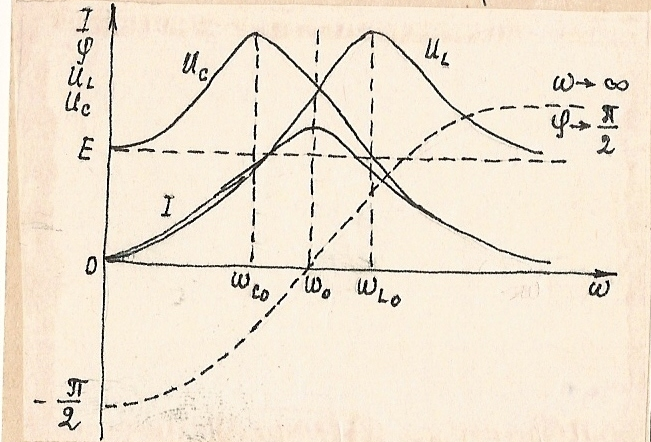
Рис.1.72. Резонансная кривая последовательного контура здесь показаны зависимости тока I, фазового сдвига тока относительно ЭДС Е, напряжений на катушке индуктивности U(l) и на конденсаторе U(c) от частоты ω.
Максимум напряжений на L и C достигается на частотах отличных от резонансной частоты ω◦L Действительно, 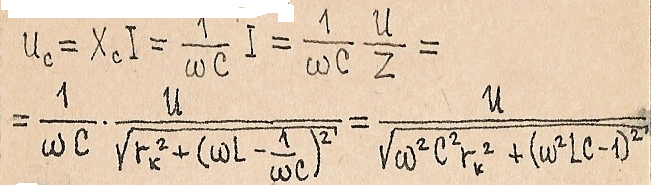
Наибольшее значение U(c) достигается ког7да знаменатель этого выражения минимален. Для определения экстремума приравняем к нулю производную от подкоренного выражения: 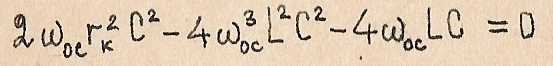
Отсюда определяем: 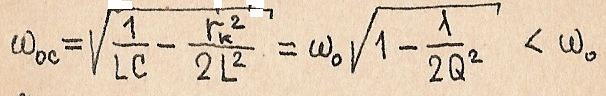
Аналогично определяем: 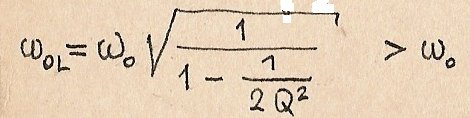
Рассмотрим обобщенную резонансную кривую контура. Пусть у- относительная величина, равная отношению модуля тока на любой частоте к его max значению
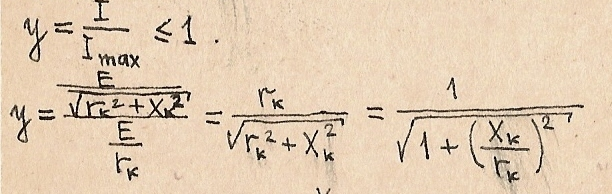
Отношение 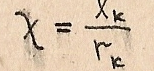 называется обобщенной расстройкой контура.
называется обобщенной расстройкой контура.
Тогда: 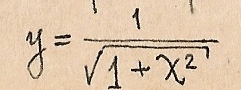
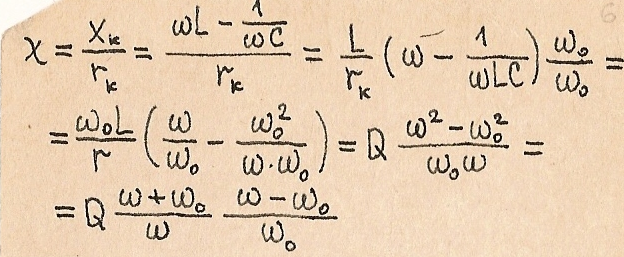
Если расстройка мала, т.е. 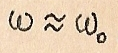 то
то 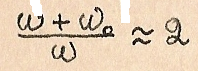
Обозначим 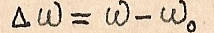 -абсолютная расстройка
-абсолютная расстройка
Тогда: 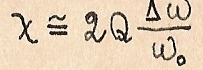
Где 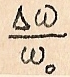 - относительная расстройка
- относительная расстройка
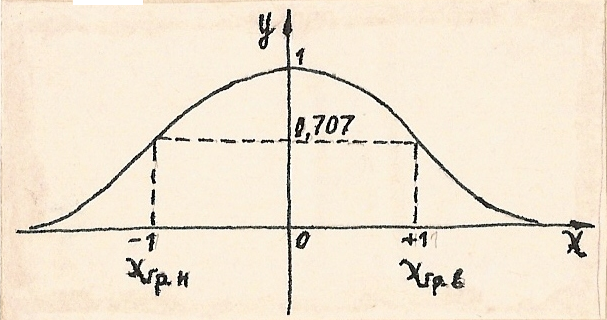
Рис.1.73. Обобщенная резонансная кривая контура:
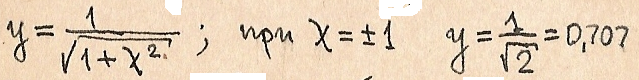
Значения обобщенной расстройки, при которых у уменьшается в 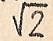 раз,
раз,
Так как 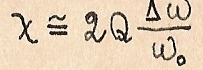 , то при λ=1
, то при λ=1 
Диапазон частот 2∆ω в котором 1>y>0,707I(ω) ток I(ω) уменьшается до уровня 0,707 I(ω◦) наз. Полосой пропускания контура . Чем больше Q, тем меньше 2∆ω.
Для регулировки резонансной частоты контура Сr.e. для его перестройки
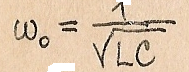
Необходимо изменить L или С.
Известно, что 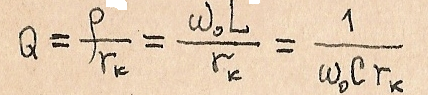
Отсюда видно, что при увеличении L добротность Q возрастает, а при увеличении С – падает.
1.3.2. Параллельный колебательный контур. Резонанс токов.
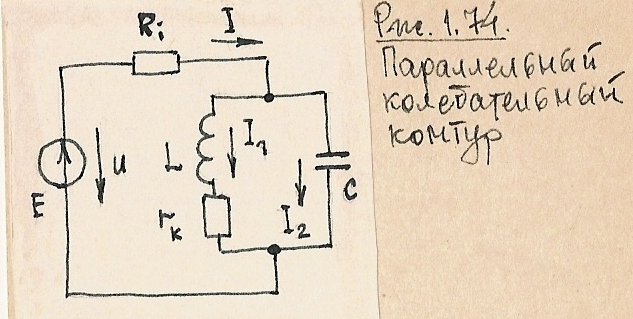
Параллельный колебательный контур (элементы L и С включены параллельно источнику ) показан на рис.1.74.
Комплекс полного сопротивления контура:
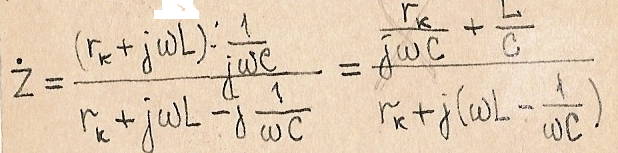
Для обеспечения резонансных свойств контура r(k) должно быть малым, поэтому слагаемым r(k)/jωC в числителе можно пренебречь
При резонансе 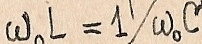 поэтому сопротивление параллельного контура на частоте резонанса
поэтому сопротивление параллельного контура на частоте резонанса 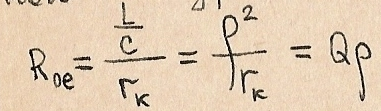
Возрастает до максимума и становится чисто активным, что подтверждается векторными диаграммами токов при 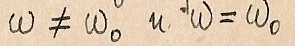
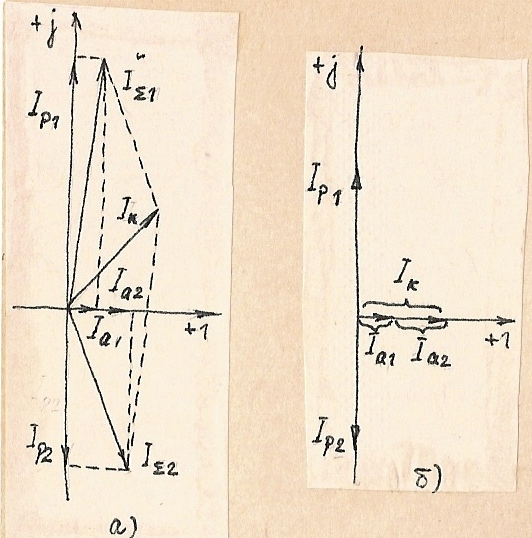
Рис.1.75. Векторные диаграммы токов для параллельного контура:
а) при отсутствии резонанса;
б) на частоте резонанса;
Активные составляющие токов I(a1),I(a2) в ветвях контура значительно меньше реактивных, т.к. проводимости значительно меньше реактивных.
При резонансе, когда 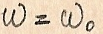 и
и 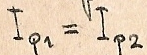 реактивные составляющие токов взаимно компенсируются и ток контура становится минимальным.
реактивные составляющие токов взаимно компенсируются и ток контура становится минимальным.
Зависимость Z(ω) для параллельного контура приведена на рис.1.76. На частоте 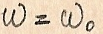 Z=R(oe). При
Z=R(oe). При 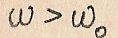 реактивное сопротивление контура носит емкостной характер, а при
реактивное сопротивление контура носит емкостной характер, а при  -индуктивный.
-индуктивный.
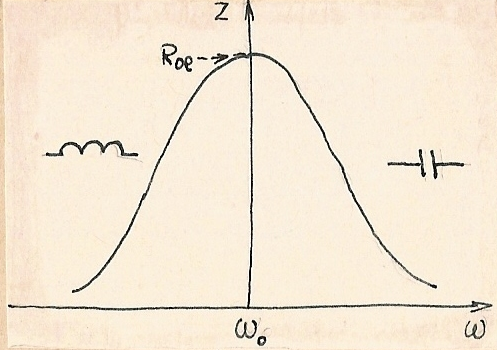
Рис.1.76. Зависимость модуля полного сопротивления параллельного контура опт частоты Z(ω).
При резонансе в параллельном контуре ток в реактивных элементах в Q раз превышает ток в цепи источника, поэтому резонанс в этом контуре называется резонансом токов.
Действительно, при 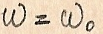 и
и 
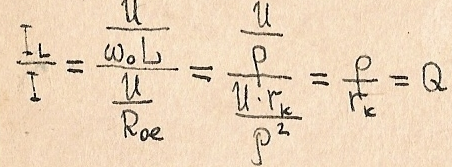
В энергетических цепях явления резонанса токов и напряжений недопустимы,
т.к. приводят к перегрузке элементов.
Колебательные контуры применяются в электронике и радиотехнике (в автогенераторах, радиоприемниках устройствах, избирательных фильтрах и т.д.).
Лекция №8
Дата добавления: 2015-06-17; просмотров: 2542;
