Нагрузка трансформатора.

Рассмотрим режим нагрузки трансформатора (рис. 1.83), когда вторичная обмотка замкнута на нагрузочное сопротивление Z_н и по ней протекает ток I₂.

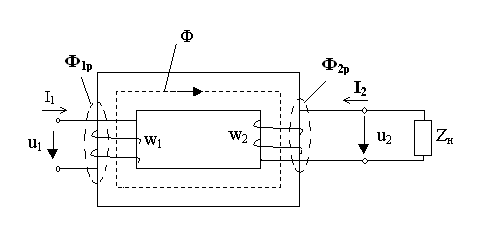
Рис. 1.83. Нагрузка трансформатора.

В этом случае можно указать следующие составляющие магнитного потока:

1. Основной поток Ф, сцепленный с первичной и вторичной обмотками.

2. Потоки рассеяния первичной и вторичной обмоток Ф_1р и Ф_2р, которые учитываются посредством введения понятий индуктивных сопротивлений рассеяния Х₁, Х₂.

Падения напряжения на активных сопротивлениях самих обмоток невелики, поэтому U₁≈E₁, U₂≈E₂.

Согласно закону полного тока магнитодвижущая сила (МДС) (это свойство тока возбуждать магнитное поле) в замкнутом магнитном контуре равна сумме падений магнитных напряжений на нем:

Hl=∑W_kI_k

где Н –напряженность магнитного поля, А/м.

l –длина средней магнитной линии сердечника.

W_k- число витков к-й катушки.

I_k – ток в к-й катушке.

Для режима х.х. трансформатора:

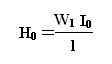
При работе трансформатора с нагрузкой:

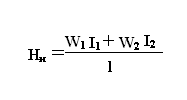
Т.к. первичное напряжение при х.х. и в режиме нагружения U₁=const, то Н₀=Н_н.

Следовательно,

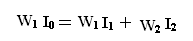
Разделив все члены этого уравнения на W₁, получим:

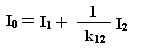
И режиме х.х. I₂=0, I₁=I₀.

В режиме нагружения во вторичной обмотке возникает ток I₂, который согласно закону Ленца препятствует причине, его вызвавшей.

Поэтому ток I₂ направлен так, чтобы размагнитить магнитопровод, т.е. навстречу I_1.

Введем понятие приведенного вторичного тока (ток вторичной обмотки, приведенных к первичной):

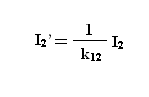
С учетом того, что направление I₂ противоположно направлению I₁ :

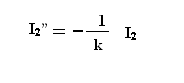
Тогда (1.15) можно записать так:

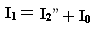
Следовательно, увеличение тока I₂ во вторичной цепи вызывает возрастание тока I₁ , потребляемого из сети первичной обмоткой.

Таким образом, трансформатор обладает свойством саморегулирования