Электрические цепи, содержащие соединения приемников
треугольником и звездой.
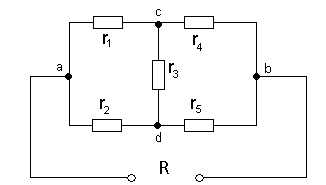
Рис.1.21. Схема эл. цепи, содержащей соединения сопротивлений треугольником и звездой.
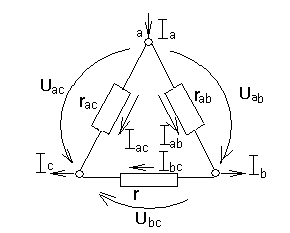

а) б)
Рис.1.22. Замена треугольника эквивалентной звездой.
Эквивалентное преобразование состоит в том, что после замены  в звезду
в звезду 
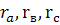 или наоборот токи
или наоборот токи 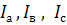 и напряжения
и напряжения  должны оставаться неизменными.
должны оставаться неизменными.
Для схемы (рис.1.22,а) по второму закону Кирхгофа
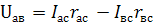
А по первому закону Кирхгофа для узла а:

Для узла в:
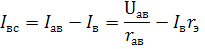
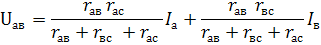
Для схемы (рис.1.22,б) по второму закону Кирхгофа
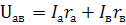
Из этих уравнений следует: 
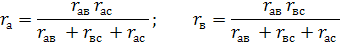
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>r</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>ас </m:t></m:r></m:sub></m:sSub></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Формулы обратной замены
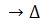
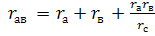

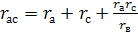
Расчет схемы рис.1.21
Заменим в схеме рис.1.21 треугольник резистором 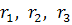 эквивалентной звездой
эквивалентной звездой 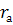 ,
, 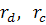 (рис.1.23).
(рис.1.23).

Рис.1.23. Эквивалентные преобразования схемы рис.1.21.
s w:val="28"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Далее схема свертывается изложенным методом.
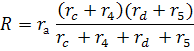
Дата добавления: 2015-06-17; просмотров: 910;
