ПРЕДСТАВЛЕНИЙ СИГНАЛОВ И ЦЕПЕЙ
9.1. Анализ цепей и устройств
Частотные характеристики электрических цепей и электронных устройств наглядно характеризуют их свойства в выбранном диапазоне частот.
 Применительно к частотным фильтрам, усилителям и преобразователям сигналов чаще всего используется их АЧХ, примеры рассмотрены в главе 6. На рис. 9.1 приведена АЧХ
Применительно к частотным фильтрам, усилителям и преобразователям сигналов чаще всего используется их АЧХ, примеры рассмотрены в главе 6. На рис. 9.1 приведена АЧХ 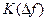 полосового фильтра,
полосового фильтра, 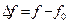 - абсолютная расстройка,
- абсолютная расстройка, 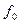 - центральная частота (частота настройки фильтра),
- центральная частота (частота настройки фильтра), 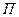 - полоса пропускания,
- полоса пропускания, 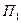 - полоса на уровне минимального коэффициента передачи
- полоса на уровне минимального коэффициента передачи 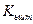 , а
, а 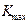 - максимальное значение ко-
- максимальное значение ко-
эффициента передачи Рис. 9.1
Как видно, АЧХ
может иметь неравномерность в полосах пропускания и удержания. Приведенное описание наглядно показывает, как фильтр пропускает или задерживает сигнал на соответствующих частотах, позволяет определить дополнительные числовые параметры фильтра, например, коэффициент прямоугольности.
На рис 9.2 показана частотная характеристика усилителя звуковых сигналов (например, в домашней стереоаппаратуре). Она должна быть достаточно равномерна в рабочей полосе частот от 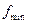 до
до 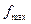 (кривая а на рис. 9.2). При усилении ре-
(кривая а на рис. 9.2). При усилении ре-
чевых сигналов 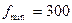 Гц и
Гц и 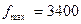 Гц, а для высококачественных музыкальных фонограмм соответственно
Гц, а для высококачественных музыкальных фонограмм соответственно 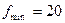 Гц и
Гц и 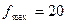 кГц. Органами регулировки тембра усилителя пользователь может искажать АЧХ усилителя, повышая усиление на нижних и верхних частотах (кривая б на рис. 9.2). В современных системах возможно изменение формы АЧХ на нескольких частотах с помощью устройства, называемого «эквалайзером», при этом форма АЧХ может отоблажаться на встроенном дисплее стереосистемы.
кГц. Органами регулировки тембра усилителя пользователь может искажать АЧХ усилителя, повышая усиление на нижних и верхних частотах (кривая б на рис. 9.2). В современных системах возможно изменение формы АЧХ на нескольких частотах с помощью устройства, называемого «эквалайзером», при этом форма АЧХ может отоблажаться на встроенном дисплее стереосистемы.
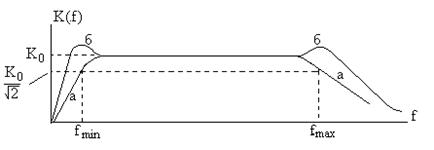
Рис. 9.2
При усилении звуковых сигналов форма ФЧХ существенного значения не имеет, так как человеческое ухо реагирует на звук энергетически, не учитывая тонкой структуры сигнала. Если же необходимо усиливать или фильтровать сигналы сложной структуры (например, телевизионные), то к ФЧХ предъявляются жесткие требования по прямолинейности, что обеспечивается специальными достаточно сложными устройствами – фазовыми корректорами..
9.2. Синтез цепей
При проектировании устройств обработки сигналов, прежде всего частотных фильтров, часто возникает задача их реализации с заданными АЧХ и, при необходимости, ФЧХ.
 Задание на синтез может определяться областью, в которую должна вписаться АЧХ проектируемого устройства, как показано на рис. 9.3.
Задание на синтез может определяться областью, в которую должна вписаться АЧХ проектируемого устройства, как показано на рис. 9.3.
Синтез цепей с заданными частотными свойствами является достаточно сложной и трудоемкой задачей, требу- Рис. 9.3
ющей применения
вычислительной техники или приведенных в литературе специальных таблиц. Сравнительно простые частотные фильтры можно синтезировать, например, с помощью программы MicroCAP (примеры приведены в главе 6).
9.3. Спектральный анализ сигналов
Анализ спектра сигнала позволяет сформулировать требования к частотным характеристикам устройств его обработки или выбрать для данного сигнала подходящее типовое устройство.
Например, пусть необходимо подобрать электронный осциллограф для исследования импульсных сигналов длительностью 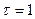 мкс. Ширина спектра сигнала равна
мкс. Ширина спектра сигнала равна 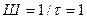 МГц, следовательно полоса пропускания входного усилителя осциллографа должна быть не менее нескольких мегагерц.
МГц, следовательно полоса пропускания входного усилителя осциллографа должна быть не менее нескольких мегагерц.
Для передачи по каналу связи телевизионного видеосигнала с шириной спектра 6,5 МГц необходимо использовать коаксиальный кабель со значительно большей полосой пропускания, а двухпроводная телефонная линия связи для этих целей не подойдет, так как ее полоса пропускания значительно меньше 6,5 МГц.
При проектировании радиоприемных устройств знание формы спектра принимаемого сигнала позволяет реализовать «согласованный фильтр», который должен пропускать сигнал в области его наиболее интенсивных спектральных компонент.
Измерение спектра наблюдаемого сигнала или отдельных его составляющих может быть необходимо в устройствах диагностики устройства, порождающего сигнал (например, двигателя автомобиля или самолета) По спектру речевого сигнала может проводиться идентификацию говорящего. Можно предложить и множество других вариантов применения спектрального анализа сигналов в технике, биомедицине и других областях.
В настоящее время широко применяется цифровая обработка различных сигналов. Она осуществляется на основе аналого-цифровых преобразователей сигналов (АЦП), цифровых вычислительных систем и цифро-аналогового преобразования (ЦАП) результата обработки. Структурная схема устройства цифровой обработки сигнала показана на рис. 9.4.
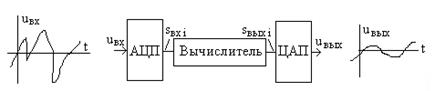
Рис. 9.4.
Входной обрабатываемый сигнал 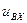 поступает на АЦП, который производит квантование (дискретизацию) сигнала по времени и уровню в моменты появления внутренних (или внешних) тактовых импульсов с частотой
поступает на АЦП, который производит квантование (дискретизацию) сигнала по времени и уровню в моменты появления внутренних (или внешних) тактовых импульсов с частотой 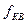 . В результате входной аналоговый (непрерывный во времени и по уровню) сигнал представляется дискретной последовательностью цифровых отсчетов
. В результате входной аналоговый (непрерывный во времени и по уровню) сигнал представляется дискретной последовательностью цифровых отсчетов 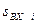 ,
, 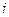 - текущий номер отсчета, поступающих на вычислитель с частотой
- текущий номер отсчета, поступающих на вычислитель с частотой 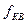 .
.
Частота квантования 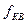 выбирается в два раза больше ширины спектра сигнала в соответствии с известной в радиотехнике теоремой Котельникова (как видно, и в этом случае необходимы спектральные представления).
выбирается в два раза больше ширины спектра сигнала в соответствии с известной в радиотехнике теоремой Котельникова (как видно, и в этом случае необходимы спектральные представления).
Вычислитель производит необходимую обработку (например, фильтрацию) поступающих отсчетов 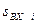 и формирует выходные отсчеты
и формирует выходные отсчеты 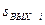 , которые поступают в ЦАП, на выходе которого появляется выходной аналоговый сигнал
, которые поступают в ЦАП, на выходе которого появляется выходной аналоговый сигнал 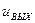 . При проектировании алгоритма обработки необходимо определять реализуемые им частотные характеристики. Рассмотренные преобразования сигнала проводятся, например, в звуковой карте (плате) персональной ЭВМ (ПЭВМ).
. При проектировании алгоритма обработки необходимо определять реализуемые им частотные характеристики. Рассмотренные преобразования сигнала проводятся, например, в звуковой карте (плате) персональной ЭВМ (ПЭВМ).
Результаты цифровой обработки могут использоваться и в цифровой форме (при этом в ЦАП необходимость отсутствует). Примером может служить спектральный анализ сигнала по поступившей последовательности (выборке) 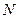 отсчетов. Он проводится с помощью цифрового алгоритма быстрого преобразования Фурье (БПФ) и результатом вычисления являются значения амплитуд (а при необходимости и начальных фаз) гармоник принятой реализации сигнала.
отсчетов. Он проводится с помощью цифрового алгоритма быстрого преобразования Фурье (БПФ) и результатом вычисления являются значения амплитуд (а при необходимости и начальных фаз) гармоник принятой реализации сигнала.
В современных музыкальных центрах и ПЭВМ при проигрывании фонограммы на экран выдается спектр амплитуд воспроизводимой реализации сигнала, после поступления следующей реализации их 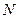 отсчетов процесс повторяется и выводится новая спектрограмма. Результаты спектрального анализа используются для создания цветомузыкальных эффектов.
отсчетов процесс повторяется и выводится новая спектрограмма. Результаты спектрального анализа используются для создания цветомузыкальных эффектов.
Для реализации цифровой обработки сигналов в реальном времени необходимы быстродействующие вычислители. Для этих целей электронная промышленность выпускает специальные сигнальные процессоры.
Спектральный анализ как встроенные функции заложен в целом ряде универсальных математических (MathCAD) и моделирующих (MicroCAP) программ, что свидетельствует о его высокой практической значимости в инженерной практи-
ке. Они будут рассмотрены в параграфе 9.5.
9.4. Прохождение сложного сигнала через
линейную цепь
В теории электрических цепей разработаны мощные методы анализа воздействия гармонического сигнала на линейную цепь (метод комплексных амплитуд).
Сложный сигнал можно представить в виде суммы гармоник и тогда имеется возможность на основе принципа наложения рассматривать воздействие на цепь каждой гармоники в отдельности с последующим сложением результатов (комплексных амплитуд).
Прохождение через цепь гармонического сигнала описывается комплексным коэффициентом передачи 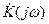 .
.
Для комплексной амплитуды 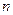 -й гармоники
-й гармоники 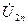 периодического сигнала
периодического сигнала 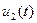 на выходе цепи получим
на выходе цепи получим
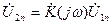 , (9.1)
, (9.1)
где 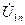 - комплексная амплитуда
- комплексная амплитуда 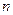 -й гармоники входного сигнала
-й гармоники входного сигнала 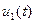 .
.
Для непериодического сигнала комплексная спектральная плотность 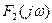 выходного сигнала
выходного сигнала 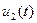 равна
равна
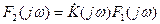 , (9.2)
, (9.2)
где 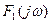 - сигнала комплексная спектральная плотность входного сигнала
- сигнала комплексная спектральная плотность входного сигнала 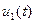 .
.
Рассмотрим четырехполюсник на рис. 9.5а при воздействии периодического сигнала, показанного на рис. 9.5б.
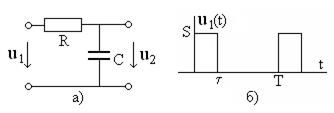
Рис. 9.5
Комплексный коэффициент передачи цепи рис. 9.5а равен
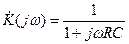 . (9.3)
. (9.3)
Комплексная амплитуда 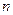 -й гармоники сигнала на рис. 9.5б определяется выражением (получите эти формулы самостоятельно)
-й гармоники сигнала на рис. 9.5б определяется выражением (получите эти формулы самостоятельно)
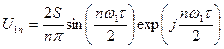 , (9.4)
, (9.4)
тогда для комплексной амплитуды 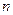 -й гармоники выходного сигнала получим
-й гармоники выходного сигнала получим
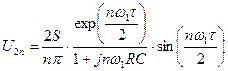 . (9.5)
. (9.5)
Рассмотрим пример расчета при 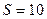 В,
В, 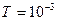 с,
с, 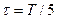 и
и 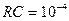 с. На рис. 9.6 показана программа расчета на языке MathCAD (повторите расчеты самостоятельно).
с. На рис. 9.6 показана программа расчета на языке MathCAD (повторите расчеты самостоятельно).
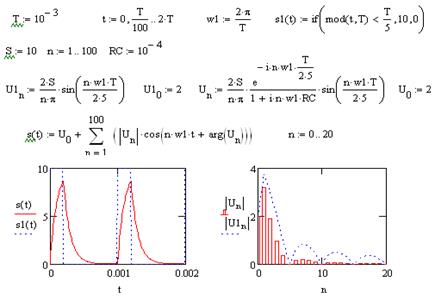
Рис. 9.6
На рис. 9.7 представлены результаты расчета выходного сигнала при малом 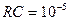 с, на рис. 9.7а приведены временные диаграммы, а на рис. 9.7б - спектры сигналов. Пунктирные линии соответствуют входному сигналу, а сплошные – выходному. На рис. 9.8 приведены аналогичные зависимости при
с, на рис. 9.7а приведены временные диаграммы, а на рис. 9.7б - спектры сигналов. Пунктирные линии соответствуют входному сигналу, а сплошные – выходному. На рис. 9.8 приведены аналогичные зависимости при 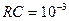 с, в тексте программы на рис. 9.6 приведены результаты при
с, в тексте программы на рис. 9.6 приведены результаты при 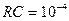 .
.
Цепь на рис. 9.5а является фильтром нижних частот, ее АЧХ показана на рис. 9.9, а полоса пропускания 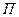 равна
равна
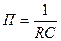 . (9.6)
. (9.6)
Как видно из рис. 9.6 – рис. 9.8, с ростом произведения 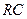 полоса пропускания фильтра уменьшается, подавляются высшие гармоники спектра сигнала, что приводит к «затягиванию» его фронта и среза и сглаживанию импульсов.
полоса пропускания фильтра уменьшается, подавляются высшие гармоники спектра сигнала, что приводит к «затягиванию» его фронта и среза и сглаживанию импульсов.
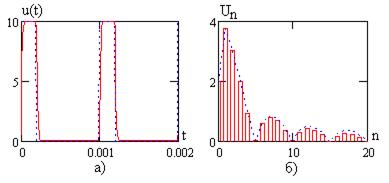
Рис. 9.7
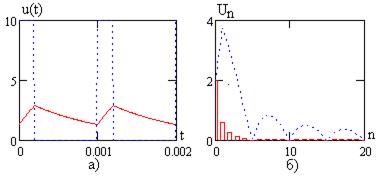
Рис. 9.8
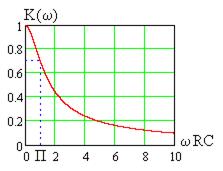
Рис. 9.9
9.5. Моделирование сигналов и цепей
Как уже отмечалось, в современных математических пакетах программ имеются встроенные функции спектрального анализа выборок отсчетов 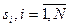 ,
, 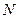 - объем выборки.
- объем выборки.
В программе MathCAD используются следующие спектральные функции.
Функция 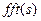 возвращает массив коэффициентов быстрого преобразования Фурье (БПФ) от заданной выборки объемом
возвращает массив коэффициентов быстрого преобразования Фурье (БПФ) от заданной выборки объемом 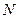 отсчетов анализируемой функции
отсчетов анализируемой функции 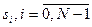 при условии, что
при условии, что
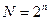 , (9.7)
, (9.7)
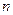 - целое число. Результатом является массив комплексных чисел
- целое число. Результатом является массив комплексных чисел 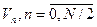 (всего
(всего 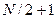 элементов), определяемых выражением
элементов), определяемых выражением
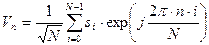 , (9.8)
, (9.8)
где 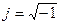 - мнимая единица. Программа, использующая функцию
- мнимая единица. Программа, использующая функцию 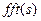 , приведена на рис. 9.10. В ней формируется прямоугольный импульс (показан на графике), выборка из
, приведена на рис. 9.10. В ней формируется прямоугольный импульс (показан на графике), выборка из 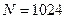 отсчетов, по которой и вычисляется функция
отсчетов, по которой и вычисляется функция 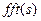 .
.
Полученные спектры амплитуд и фаз представлены на рис. 9.9. Как видно, амплитуды гармоник не соответствуют результатам расчета на основе ряда Фурье.
По полученным с помощью функции 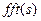 величинам
величинам 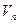 амплитуды
амплитуды 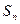 и начальные фазы
и начальные фазы 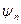 гармоник определяются выражениями
гармоник определяются выражениями
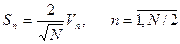 , (9.9)
, (9.9)
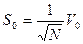 , (9.10)
, (9.10)
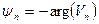 . (9.11)
. (9.11)
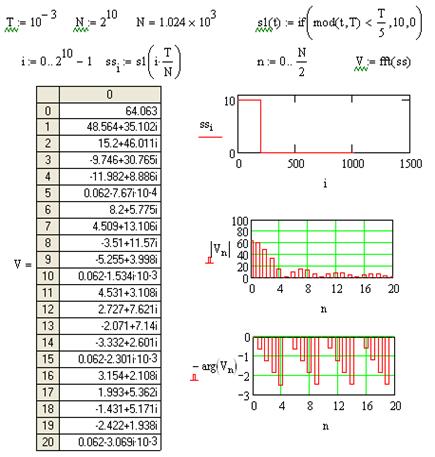
Рис.9.10
Обратное преобразование Фурье (суммирование ряда Фурье) выполняется функцией 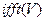 в соответствии с выражением
в соответствии с выражением
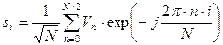 , (9.12)
, (9.12)
Эту функцию необходимо использовать только с результатами, даваемыми функцией 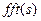 , а не с правильными комплексными амплитудами гармоник сигнала,
, а не с правильными комплексными амплитудами гармоник сигнала,
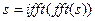 , (913)
, (913)
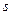 - выборка отсчетов сигнала.
- выборка отсчетов сигнала.
Функция 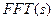 (в MathCADе строчные и прописные символы различны) реализует вычисления БПФ в соответствии с выражением
(в MathCADе строчные и прописные символы различны) реализует вычисления БПФ в соответствии с выражением
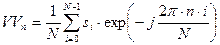 , (9.14)
, (9.14)
а функция 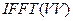 - соответственно
- соответственно
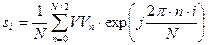 . (9.15)
. (9.15)
При этом амплитуды и начальные фазы гармоник сигнала будут равны:
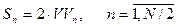 , (9.16)
, (9.16)
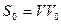 , (9.17)
, (9.17)
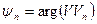 . (9.18)
. (9.18)
Таким образом, программа MathCAD позволяет проводить расчеты спектров сигналов, частотных характеристик цепей и получать временные реализации процессов на выходе электри-
ческих цепей.
Спектральный анализ сигналов можно проводить с использованием программ схемотехнического моделирования, например, MicroCAP.
В пакете предусмотрены следующие функции спектрального анализа.
Функция HARM(v(1)) определяет амплитуды гармоник напряжения v(1) (или другого напряжения или тока), отображая в режиме Transient Analysis соответствующий спектр амплитуд.
Функция FFT(v(1)) реализует БПФ напряжения v(1) и отличается от HARM(v(1)) тем, что амплитуды гармоник умножаются на 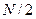 , а постоянной составляющей – на
, а постоянной составляющей – на 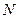 .
.
Функция PHASE(V) определяет фазы гармоник 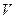 , вычисленных с помощью функции FFT.
, вычисленных с помощью функции FFT.
 На рис. 9.11 показана модель простейшей RC цепи, на которую воздействует импульсный источник напряжения вида рис.9.4б с периодом повторения
На рис. 9.11 показана модель простейшей RC цепи, на которую воздействует импульсный источник напряжения вида рис.9.4б с периодом повторения 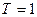 мс и длительно-
мс и длительно-
Рис. 9.11 стью импульса 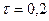 мс.
мс.
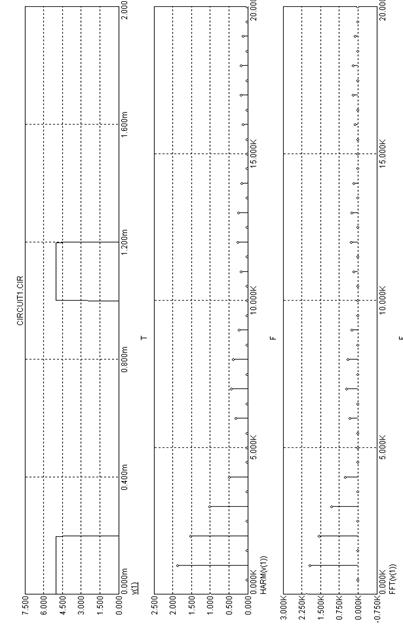
На рис. 9.12 приведены результаты моделирования входного сигнала и его спектров с использованием функций HARM(v(1)) и FFT(v(1)). Для спектрального анализа могут быть использованы обе функции, однако физические результаты дает функция HARM(v(1)).
На рис. 9.13 приведены входной и выходной сигналы цепи рис. 9.10 (верхний график), а затем их спектры амплитуд. Как видно, рассматриваемый фильтр нижних частот подавляет высшие гармоники в спектре выходного сигнала, что приводит к его сглаживанию во временной области.
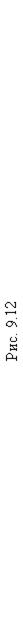
Дата добавления: 2015-06-17; просмотров: 1113;
