Нала во времени.

Вычислим аргументы обеих частей выражения (7.30),

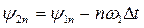, (7.37)

то есть начальные фазы гармоник сигнала при временной задержке уменьшаются на величину 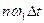, которая зависит от номера гармоники, периода сигнала (частоты его первой гармоники) и величины задержки .

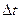Для доказательства теоремы смещения запишем

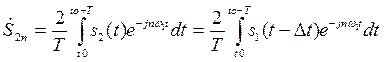. (7.38)

Проведем замену переменных 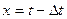, тогда получим

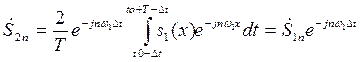. (7.39)

На спектральные характеристики влияют свойства симметрии сигнала.

Рассмотрим четные функции времени, удовлетворяющие условию 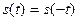. В этом случае амплитуда квадратурной составляющей 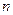-й гармоники равна нулю

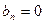, (7.40)

комплексная амплитуда 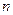-й гармоники 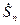является действительным числом,

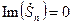, (7.41)

а начальная фаза равна 0 или 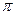в зависимости от знака .

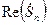Для нечетной функции, удовлетворяющей условию 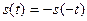, амплитуда синфазной составляющей 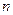-й гармоники равна нулю

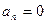, (7.42)

комплексная амплитуда 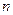-й гармоники 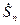является мнимымчислом,

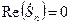, (7.43)

а начальная фаза равна 0 или 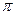в зависимости от знака .

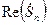Эти свойства иллюстрирует пример четного сигнала на рис. 7.2, для которого имеет место равенство (7.19). Его фазовый спектр со значениями 0 или 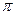показан на рис. 7.3б.

Рассмотрим комплексные спектры двух сигналов 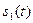(рис. 7.11а) и 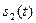(рис. 7.11б), и их сумму 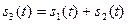(рис. 7.11в).

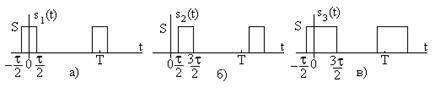
Рис. 7.11.

Сигнал 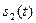получен из 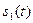сдвигом во времени на

величину 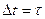, оба являются последовательностями прямоугольных импульсов длительностью импульса 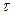. Сигнал 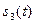оказывается последовательностью прямоугольных импульсов длительностью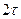

Комплексная амплитуда 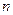-й гармоники 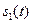определена ранее (7.31) и равна

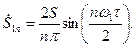(7.44)

По теореме смещения можно найти комплексную амплитуду 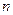-й гармоники сигнала 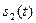в виде

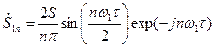. (7.45)

Тогда согласно свойству линейности комплексная амплитуда 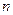-й гармоники сигнала 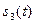равна

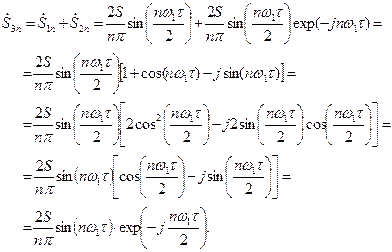(7.46)

С другой стороны, при прямом вычислении (проведите расчеты самостоятельно) комплексная амплитуда 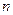-й гармоники сигнал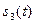а равна

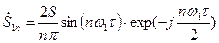, (7.47)

что полностью совпадает с (7.46).

7.8. Мощность периодического сигнала

Пусть имеется сигнал 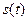(ток или напряжение) в сопротивлении 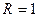Ом, тогда средняя мощность сигнала равна

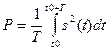. (7.48)

Эту же величину можно выразить через гармоники сигнала с помощью равенства (теоремы) Парсеваля в виде

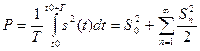. (7.49)

С помощью спектральных характеристик можно определить действующее значение 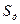сигнала в виде

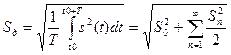. (7.50)

7.9. Ширина спектра

Как видно по графикам спектров амплитуд рассмотренных сигналов, в целом наблюдается тенденция уменьшения

амплитуд гармоник с ростом их номера (частоты). Графики на рис. 7.5 показывают, что форма сигнала определяется сравнительно небольшим числом гармоник. Все это свидетельствует

о том, что для представления (даже достаточно точного) сигнала необходимо учитывать ограниченное число гармоник, которые занимают конечный интервал частот.

Мощность сигнала определяется выражением (7.39). Для рассматриваемых видеосигналов наиболее интенсивные гармоники имеют номера от 1 до некоторой величины N, при этом их суммарная мощность равна

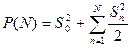. (7.51)

Как видно, с ростом 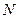мощность 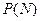увеличивается, и при 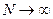стремится к полной мощности .

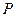Тогда можно определить число гармоник 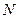, при котором мощность 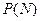будет равна величине 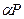, с помощью

выражения

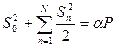. (7.52)

В результате можно определить ширину спектра 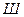в виде

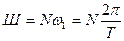. (7.53)

В качестве примера рассмотрим последовательность прямоугольных импульсов, показанную на рис. 7.2 со спектром амплитуд, показанном на рис. 7.3а. (скважность импульсов 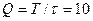) Зависимость нормированной мощности 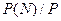от числа учитываемых гармоник показана на рис. 7.12. Как видно, функция 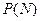является неубывающей и достигает уровня 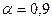при 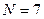( 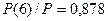, 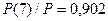), тогда ширина спектра сигнала определяется выражением (7.44).

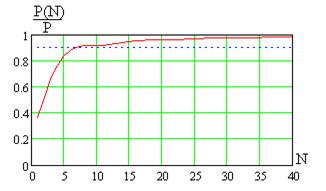
Рис. 7.12

Этот же график в области значений от 0,9 до 1 показан на рис. 7.13. С ростом 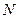кривая очень медленно приближается к 1 и достигает значения 0,99 уже при .

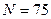В инженерной практике рассмотренный расчет ширины спектра проводится редко, а используется ее инженерная оценка. Для импульсных сигналов с длительностью 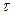(на-

пример, рис. 7.2) ширина спектра определяется выражением

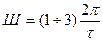(рад/с) или 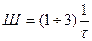(Гц) (7.54)

(сравните эти величины со значениями нулей огибающей спектра амплитуд).

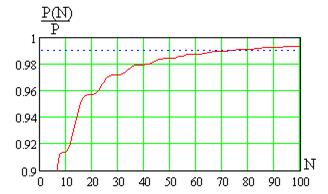
Рис. 7.13

Множитель от 1 до 3 косвенно характеризует долю мощности сигнала, заключенную в полосе пропускания (единица примерно соответствует 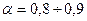, а тройка - величине 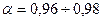, эти значения зависят от формы импульса).

Оценки ширины спектра можно выразить через число гармоник,

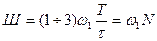, (7.55)

где 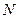требуемое число гармоник, равное

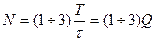. (7.56)

На практике чаще всего используются соотношения с единичным множителем вида

В рассмотренном примере сигнала на рис. 7.2 скважность 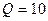и для обеспечения 90% мощности необходимо учитывать 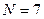гармоник (рис. 7.12), по оценке (7.58) требуется учитывать 10 гармоник.

7.10. Задания для самостоятельного решения

Задание 7.1. Определите и постройте графики спектров амплитуд и фаз сигналов вида:

,

,

,

,

.

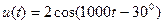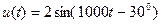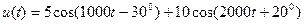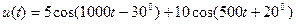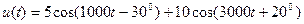Задание 7.2. Определите спектры амплитуд и фаз сигналов, показанных на рис. 7.14, постройте их графики. Проведите расчет ширины спектра пр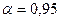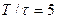и , и 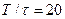, сравните полученные результаты.

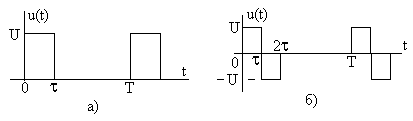
Рис. 7.14

Задание 7.3. С помощью теоремы смещения проведите расчет спектров амплитуд и фаз сигнала, показанного на рис. 7.14а, воспользовавшись результатами, полученными для сигнала на рис.7.2.

Задание 7.4. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.15, постройте их графики. Сравните спектр амплитуд со спектром гармонического сигнала, проанализируйте результаты.

Вычислите ширину спектра сигнала при 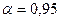. Чем обусловлены наблюдаемые различия в ширине спектра для сигналов, показанных на рис. 7.14а и рис. 7.15? Как в полученных результатах проявляются свойства симметрии сигнала?

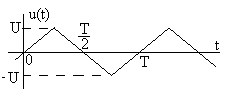
Рис. 7.15

Задание 7.5. Определите спектры амплитуд и фаз сигналjd, показанного на рис.7.16, постройте их графики.

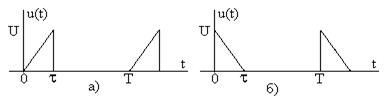
Рис. 7.16

Задание 7.6. Определите спектры амплитуд и фаз сигнала, показанного на рис.7.17, постройте их графики.

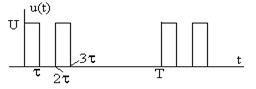
Рис. 7.17

Проведите тот же расчет, представив сигнал на рис. 7.17 в виде суммы двух импульсных последовательностей, показанных на рис. 7.18, и используя свойство линейности.

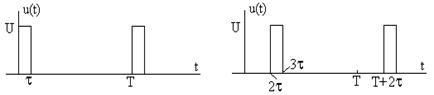
Рис. 7.18