ос күштің баламалығы туралы теоремалар

1-теорема.Денеге әсерін сақтай отырып, қос күшті өзінің әсер ету жазықтығында жататын моменті берілген қос күш моментіне тең, басқа күшпен алмастыруға болады.

Қатты дененің С және D нүктелерінде (5.4-сурет) иіні һ₁-ге тең (Ғ_, Ғ^,) қос күші түсірілген делік. Теореманы дәлелдеу үшін, дененің кез-келген Е және L нүктелерінен бір-бірінен һ₂ қашықтығында орналасқан екі параллель түзулерді Ғ және Ғ^, күштерінің әсер ету сызықтарымен А және В нүктелерінде қиылысқанша созайық. Ғ және Ғ^, күштерін әсер ету сызықтарының бойымен А және В нүктелеріне көшірейік. Үшінші аксиомадан шығатын салдар бойынша Ғ және Ғ^, күштерінің денеге әсері өзгермейді. Енді Ғ күшін АВ және АL, Ғ^, күшін АВ және ВЕ бағыттарында P, Q және P^/, Q^/ құраушыларына жіктейміз, яғни Ғ =P+Q, Ғ^/ =P^/+Q^/. Ғ және Ғ^, күштерінің модульдері өзара тең және бағыттары параллель екендігінен P= P ^/ және Q= Q^/ болады. Q және Q^/ күштерін бір түзудің бойымен қарама-қарсы бағытталып теңескен күштер жүйесін құрайтындықтан үшінші аксиома бойынша алып тастаймыз да, Р және Р^/ күштерін өздерінің әсер ету сызықтарының бойында жатқан L және E нүктелеріне көшіреміз. Соның нәтижесінде берілген (Ғ_, Ғ^,) қос күш (Р, Р^/) қос күшімен алмасады.

Осы екі қос күштің моменттері тең екендігін дәлелдеу үшін, Вариньон теоремасын қолданамыз:

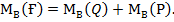
Күш моменттерінің модулі:

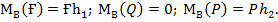
Олай болса

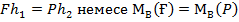
Сонымен, денеге әсер ететін (Ғ_, Ғ^,) қос күшін моменті берілген қос күш моментіне тең басқа (Р, Р^/) өос күшімен алмастыруға болатынын дәлелдедік.

Дәлелденген теоремадан қос күштің мынадай қасиеттерін атап кетуге болады:

1. Қос күштің денеге әсерін өзгертпей, өзінің әсер ету жазықтықтығында кез-келген орынға көшіруге болады.

2. Берілген жұптың моментін сақтай отырып қос күштің денеге әсерін өзгертпей. Жұпты құрайтын күштердің модулін және иінін өзгертуге болады.

Қос күштің осы қасиеттерінен бір жазықтықта орналасқан екі жұп, моменттерініңшамасы мен дененің бұрылу бағыты бірдей болғанда бір-біріне баламалы болатынын көруге болады.

Жоғарыда дәлелденген теоремалар қос күштің денеге әсері оның моментімен сипатталатынын көрсетеді.

Берілген жазықтықта жататын қос күшті оның моментімен берген жеткілікті, жұп күшінің шамасы мен иіні және жұптың әсер ету жазықтығының қай жерде орналасқаны өзекті мәселеге жатпайды. Сондықтан есеп шығарған кезде суретте көбінесе жұп күштерін бейнелемей-ақ, қос күшті оның денені айналдыру бағытымен бағытталған доғалық нұсқамамен көрсетеді. Мысалы, 5.5-суретте денеге әсер ететін Ғ күші мен моменті m қос күш көрсетілген.

2-теорема.Қос күшті өзінің әсер ету жазықтығынан оған параллель тасымалдағаннан қос күштің денеге әсері өзгермейді.

Қатты денеге Н₁ жазықтығында жататын иіні АВ-ға тең (Ғ_, Ғ^,) қос күші әсер етеді делік (5.6-сурет) Н₁-ге параллель жүргізілген Н₂ жазықтығында ұзындығы АВ-ға тең және оған параллель СД кесіндісін алайық. С жәнеД нүктелерінде модульдері берілген жұп күштеріне тең және параллель теңескен 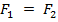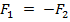^/; күштерін түсіреміз. Н₁ және Н₂ жазықтықтарында орналасқан қос күштердің иіндерін АВ=СД деп аламыз. Параллель күштерді қосу ережесі бойынша модульдері өзара тең және бірыңғай параллель бағытталған Ғ және Ғ₂ күштерінің тең әсер етуші R күші оған параллель және АД кесіндісінің ортасы О нүктесі арқылы Ғ және Ғ₂ күштерінің әсер ету жағына қарай бағытталады. R күшінің модулі R=2Ғ. Модульдері өзара тең және бірыңғай Ғ және Ғ₂ параллель күтерінің тең әсер етуші R күші оларға параллель және ВС кесіндісінің ортасы О нүтесі арқылы осы күштердің бағытымен бағыттас болады. Тең әсер етуші R күшінің модулі R=2Ғ.

5.6-суретте АВСД фигурасы параллелограмм болғандықтан, АД және ВС диагональдары қиылысу О нүктесінде қақ бөлінеді. О нүктесіне түсірілген модульдері өзара тең және қарама-қарсы бағытталған R және R^/ күштерін теңескен күштер жүйесі болғандықтан алып тастауға болады. Соның нәтижесінде Н₁ жазықтығында жататын (Ғ_1, Ғ₁^,) қос күші Н₂ жазықтығында жататын дәл осындай (Ғ_1, Ғ₁^,) қос күшімен алмастырылады.

Осы жерде мынадай ұқсастықты атап кеткен жөн. Қатты денеге әсер ететін күш модулімен, әсер ету сызығымен және әсер ету сызығының бойындағы мүмкін болатын дене қозғалысының бағытымен анықталады. Күштің түсу нүктесін әсер ету сызығының бойымен кез келген нүктеге көшіруге болады. Қатты денеге әсер ететін қос күш оның моментінің модулімен, әсер ету жазықтығымен және айналу бағытымен анықталады. Қос күшті әсер ету жазықтығында кез келген орынға көшіруге болады. Қатты дененің қос күш әсерінен қандай қозғалыста болатыны динамика бөлімінде зерттеледі.