ОЦЕНКА ТОЧНОСТИ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЙ

Цель работы -обработать данные прямых и косвенных измерений физических величин.

Теоретические основы лабораторной работы

В методике данной лабораторной работы использованы теоретические основы оценки погрешности прямых и косвенных измерений, представленные в разделе Обработка результатов измерений в физическом эксперименте. Кроме этого в методике эксперимента используются законы и соотношения теории постоянного тока, что позволяет проводить измерения не только механических, но и электрических физических величин.

. В соответствии с законом Ома для однородного (с точки зрения отсутствия сторонних сил) участка цепи, сила тока I, текущего по металлическому проводнику определяется по формуле

I = 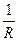U

Коэффициент пропорциональности в законе Ома 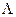= 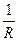называется электрической проводимостью проводника. Физическая величина R – сопротивление проводника.

Сопротивление однородного цилиндрического проводника R зависит от его формы, размеров, а также свойств материала, из которого он изготовлен

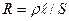(1.1)

здесь: U - падение напряжения на проводнике, 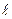- длина проводника; S - площадь его поперечного сечения; r - удельное сопротивление.

Удельное сопротивление характеризует способность вещества проводить электрический ток и зависит от химической природы вещества и условий, в которых находится проводник.

Из формулы (1) очевидно, что

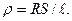
Площадь поперечного сечения S рассчитывается по формуле 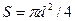с использованием измеренного значения диаметра d. Сопротивление R = U/ I вычисляется по измеренным значениям напряжения U и тока I в цепи согласно закону Ома.

Таким образом, значение удельного сопротивления можно вычислить по формуле

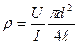(1.2)

Каждую из физических величин, входящих в формулу (1.2) можно измерить непосредственно соответствующими приборами (прямые измерения). Величина удельного сопротивления непосредственно не измеряется, а вычисляется по формуле (косвенные измерения).

Величины 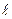, d, U и I измеряются соответствующими приборами с определенной точностью. В общем случае результат любого измерения величины х представляют в виде

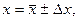
где 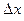- погрешность или ошибка в измерениях х.

Измерения длины 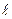и диаметра d проволоки проводится с использованием маркированных шкал линейки, штангенциркуля и микрометра. Погрешность измерения линейкой определяется как половина цены наименьшего деления. Погрешность измерения штангенциркулем и микрометром указана на приборах.

Вероятно, что диаметр не одинаков по всей длине проволоки. Если измерения проводятся штангенциркулем или более грубо линейкой, то почувствовать незначительные изменения диаметра проволоки невозможно, так как погрешность указанных приборов достаточно велика. В этом случае величину d следует воспринимать, как результат однократного измерения со средней величиной 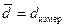и с поправкой Dd, принятой за точность прибора.

Измеряя диаметр более точным прибором, например микрометром, получим серию результатов: 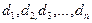, где n - число измерений. Как величина случайная диаметр варьирует около некоторого среднего значения, которое определяется как среднее арифметическое:

.

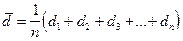Величина средней абсолютной погрешности прямых измерений диаметра проволоки

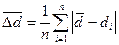(1.3)

В случае, если она меньше точности используемого прибора, то за величину абсолютной ошибки следует принять погрешность прибора.

Измерения величины тока I и напряжения U проводят с помощью электроизмерительных приборов (амперметра и вольтметра). Точность этих приборов характеризуют приведенной погрешностью

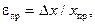
где х_пр - наибольшее значение электрической величины(I или U), которое может быть измерено по шкале прибора.

Приведенная погрешность, измеренная в процентах, определяет класс точности прибора (указан на шкале).

Абсолютная погрешность физической величины, измеренной данным прибором в любом месте шкалы

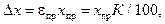(1.4)

где К - класс точности прибора.

Какова же будет средняя абсолютная погрешность косвенного определения удельного сопротивления 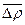по результатам прямых измерений величин, входящих в формулу (2)?

Среднее значение удельного сопротивления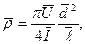

Относительная погрешность косвенного измерения удельного сопротивления

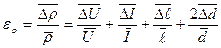(1.5)

Средняя абсолютная погрешность косвенного измерения удельного сопротивления

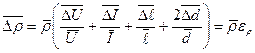(1.6)

Погрешности в определении r, определенные формулами (5) и (1.6), представляют собой верхний предел систематических и случайных ошибок. Но погрешности, рассчитанные на основании указанных правил, могут быть неоправданно завышенными.

Считается, что если погрешности прямых измерений каждой из определяемых величин (в нашем случае I, U, 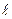и d) независимы, случайны и подчиняются нормальному закону распределения, то более реалистичной (и меньшей) оценкой окончательной погрешности результата измерения является средняя квадратичная ошибка s.

В нашем случае при прямых однократных измерениях I, U и 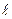за среднюю квадратичную ошибку принимается погрешность прибора. Результаты прямых многократных измерений диаметра проволоки будут иметь среднюю квадратичную ошибку среднего значения

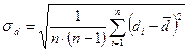(1.7)

При косвенных измерениях средняя квадратичная погрешность измерения 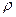вычисляется по формуле:

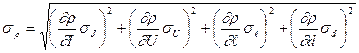(1.8)

где 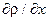- частная производная функции r(I, U, 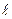, d) по каждой из переменных, рассчитанная по средним значениям прямых измерений:

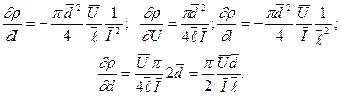
(1.9)

В результате подстановки выражений (1.9) в уравнение (1.8) получим

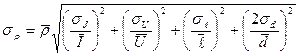(1.10)

Электрическая схема

Для определения удельного сопротивления отрезка проволоки используется простейшая электрическая цепь (см. рисунок 1.1), которая состоит из источника тока e, амперметра A, вольтметра V и исследуемого участка ВС.