Периодический режим в однородной линии
При периодическом режиме под действием приложенного гармонического напряжения в любой точке линии напряжение и ток изменяются гармонически с частотой источника.
Обозначим комплексные действующие значения напряжения и тока на расстоянии x от начала линии через U = U(x) и I = I(x)
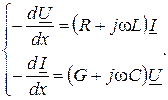 (13.4)
(13.4)
Так как комплексные величины U и I не зависят от времени t и являются только функциями расстояния x, то в уравнении (13.4) частные производные заменены обыкновенными.
Продифференцировав систему (13.4) по расстоянию x, получим отдельные уравнения относительно тока и напряжения
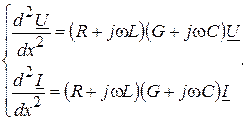 (13.5)
(13.5)
Введем обозначение
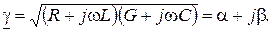 (13.6)
(13.6)
Величина g называется коэффициентом распространения волны. Тогда
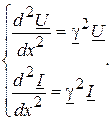 (13.7)
(13.7)
В результате получили однородные линейные дифференциальные уравнения второго порядка одного вида.
Решение первого из них имеет вид:
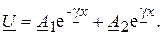 (13.8)
(13.8)
Ток I проще всего находится подстановкой последнего уравнения в первое уравнение системы (13.4).
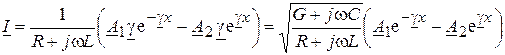
или
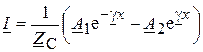 , (13.9)
, (13.9)
где 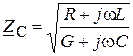 (13.10)
(13.10)
носит название волнового сопротивления линии.
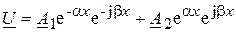 (13.11)
(13.11)
Мгновенное значение напряжения в точке x равно мнимой части выражения 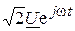 .
.
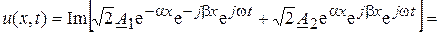
 (13.12)
(13.12)
где y1 и y2 – аргументы комплексных чисел A1 и A2.
Таким образом, мгновенное значение напряжения в любой точке имеет две составляющие.
Рассмотрим первую из них.
Если считать точку x фиксированной и рассматривать изменение напряжения в данной точке в зависимости от времени, то первая составляющая в выражении (13.12) представляет собой гармоническую функцию с постоянной амплитудой.
Если же считать момент t фиксированным и рассматривать изменение мгновенного напряжения вдоль линии (т.е. в зависимости от расстояния x), то получим затухающую гармоническую волну напряжения, амплитуда которой 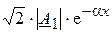 убывает с ростом х, т.е. по мере удаления от начала линии.
убывает с ростом х, т.е. по мере удаления от начала линии.
Величина a, характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом затухания, а величина b, характеризующая изменение фазы на единицу длины линии, называется коэффициентом фазы.
Убывание амплитуды волны вдоль линии обусловлено потерями в линии, а изменение фазы – конечной скоростью распространения электромагнитных колебаний.
На рис. 13.2 изображены волны напряжения, соответствующие двум следующим друг за другом моментами времени t1 и t2.
Расстояние между двумя ближайшими точками, взятое в направлении распространения волны, фазы колебаний напряжения различаются на 2p, называется длиной волны – l
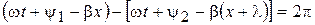 ,
,
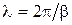 . (13.13)
. (13.13)
С течением времени волна перемещается от начала линии к ее концу. Она называется прямой или падающей волной.
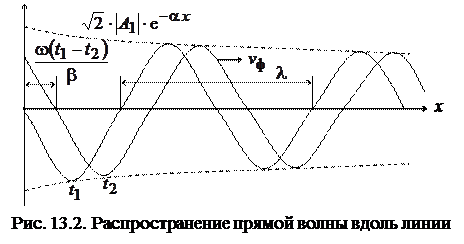 |
Дата добавления: 2015-06-17; просмотров: 845;
