Функции и способы их задания.

Пусть X и Y некоторые множества.

Определение 2.1.Функцией называется отношение (соответствие) f между множествами X и Y, при котором каждому элементу x 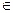X соответствует единственный элемент y 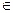Y. Множество X называют областью определения функции и обозначают D(f), а множество {f(x)} 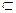Y – областью или множеством значения функции и обозначают E(f).

Определение 2.2.Переменную x 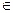D(f)называют независимой переменной или аргументом, а y 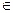E(f) называют зависимой переменной или функцией.

Определение 2.3.Если X и Y – числовые множества, то y=f(x) называется числовой функцией.

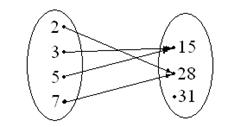Пример 2.4.Пусть даны два множества X={2;3;5;7}, Y={15;18;31}. Установим между ними такое соответствие: элемент x 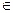X является делителем элемента y 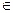Y. Тогда каждому элементу множества X соответствует только один элемент множества Y: 2 28; 3 15; 5 15; 7 28. Следовательно, задана функция.

Существуют три способа задания функции: аналитический, графический и табличный.

Если указана совокупность операций, которые нужно произвести над аргументом x, чтобы получить значение функции, то говорят, что функция задана аналитическим выражением.

Примером могут служить функции y=x²-5x+1, x 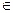[0,1], y=x²+7x-1, x 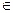( 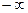; 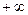). Они заданы на различных множествах.

Функция может задаваться на различных числовых множествах различными аналитическими выражениями, например

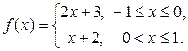
Эта функция определена [-1;1]. Для вычисления значения функции нужно выяснить, каким аналитическим выражением следует воспользоваться для заданного конкретного значения аргумента.

Определение 2.5.Множество из n элементов {a₁, a₂, …, a_n}, для каждого из которых установлено, какой является 1-м, 2-м, …, n-м, называется упорядоченной n-кой (a₁, a₂, …, a_n).

Определение 2.6.Множество упорядоченных пар действительных чисел, т.е. {(x;y) | x 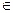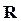, y 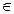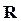}, называется числовой плоскостью. Обозначают ее .

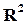Способ задания функции с помощью графика на координатной плоскости называется графическим.

При табличном способе задания функции приводится таблица, в которой даются значения функции для конечного множества значений аргумента.