Свойства вероятности
Свойство 7.1. Вероятность невозможного события равна 0: Р(Ø)=0.
Свойство 7.2. Вероятность достоверного события равна 1: Р(Ω)=1.
Свойство 7.3. Для любого события А верно, что 0 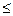 Р(А)
Р(А) 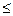 1.
1.
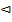 Р(А)=
Р(А)= 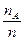 . Т.к. 0
. Т.к. 0 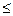
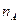
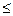 n, то 0
n, то 0 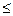
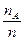
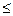 1, следовательно 0
1, следовательно 0 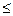 Р(А)
Р(А) 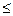 1.
1. 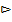
Свойство 7.4. (теорема сложения вероятностей) Если события А и В несовместимы, то вероятность их суммы равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).
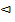 Р(А+В)=
Р(А+В)= 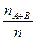 =
= 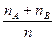 =
= 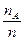 +
+ 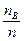 = Р(А)+Р(В).
= Р(А)+Р(В). 
Свойство 7.5. (обобщённая теорема сложения вероятностей)
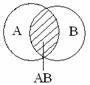 Р(А
Р(А 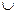 В)= Р(А)+Р(В)-Р(АВ).
В)= Р(А)+Р(В)-Р(АВ).
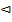 Р(А
Р(А 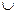 В)=
В)= 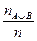 =
= 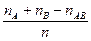 =
= 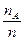 +
+ 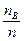 -
- 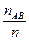 = =Р(А)+Р(В)-Р(АВ).
= =Р(А)+Р(В)-Р(АВ). 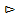
Свойство 7.6. (теорема сложения k слагаемых) Если события 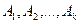 попарно несовместимы, то Р(
попарно несовместимы, то Р( 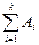 )=
)= 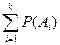 .
.
Свойство 7.7. Если событие А влечёт В (А 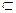 В), то Р(А)
В), то Р(А) 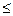 Р(В).
Р(В).
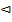 В=А+(В\А), Р(В)= Р(А)+Р(В\А)
В=А+(В\А), Р(В)= Р(А)+Р(В\А) 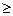 Р(А).
Р(А). 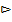
Свойство 7.8. Если событие А влечёт В (А 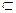 В), Р(В\А)=Р(В)-Р(А)
В), Р(В\А)=Р(В)-Р(А)
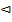 из предыдущего свойства
из предыдущего свойства 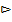
Свойство 7.9. Вероятность события, противоположного событию A вычисляется по формуле: Р(Ā)=1-Р(А). A +Ā= Ω.
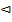 Ā = Ω\ A, Р(Ā)=Р(Ω) - Р(A) = 1 - Р(A), т.к. A
Ā = Ω\ A, Р(Ā)=Р(Ω) - Р(A) = 1 - Р(A), т.к. A 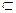 Ω.
Ω. 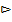
Свойство 7.10. Если события H1,H2,…,Hk образуют полную группу, то
Р(H1)+P(H2)+…+ Р(Hk)=1.
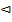 по определению полной группы H1+ H2+… +Hk=Ω, тогда по свойству 6 Р(
по определению полной группы H1+ H2+… +Hk=Ω, тогда по свойству 6 Р( 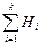 )=(
)=( 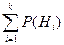 )= Р(Ω)=1.
)= Р(Ω)=1. 
Дата добавления: 2015-06-17; просмотров: 998;
