Геометрические вероятности
I. Геометрическая вероятность на прямой.
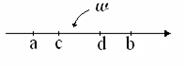 Пусть на числовой оси имеется отрезок [a,b] и на него наудачу бросается точка. Вероятность того, что эта точка попадёт на [c,d]
Пусть на числовой оси имеется отрезок [a,b] и на него наудачу бросается точка. Вероятность того, что эта точка попадёт на [c,d] 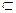 [a,b], вычисляется по формуле:
[a,b], вычисляется по формуле:
Р{ω 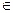 [c,d]}=
[c,d]}= 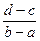 – геометрическая вероятность на прямой.
– геометрическая вероятность на прямой.
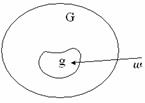
II. Геометрическая вероятность на плоскости.
Пусть на плоскости фигура g составляет часть фигуры G. Вероятность того, что наудачу брошенная в фигуру G точка попадёт в фигуру g 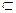 G находится по формуле:
G находится по формуле:
Р{ ω 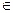 g}=
g}= 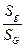 – геометрическая вероятность на плоскости.
– геометрическая вероятность на плоскости.
Здесь 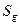 и
и 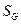 – площади фигур g и G соответственно.
– площади фигур g и G соответственно.
III. Геометрическая вероятность в пространстве.
Пусть в пространстве ( 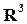 ) имеется фигура d, составляющая часть фигуры D. Вероятность того, что наудачу брошенная в фигуру D точка попадёт в фигуру d, определяется по формуле:
) имеется фигура d, составляющая часть фигуры D. Вероятность того, что наудачу брошенная в фигуру D точка попадёт в фигуру d, определяется по формуле:
Р {ω 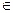 d}=
d}= 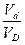 - геометрическая вероятность в пространстве.
- геометрическая вероятность в пространстве.
Здесь 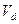 и
и 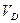 – объёмы фигур d и D соответственно.
– объёмы фигур d и D соответственно.
Замечание 6.1. Геометрические вероятности позволяют устранить недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом элементарных исходов.
Пример 6.2.(задача о встрече) Два студента условились встретиться в определённом месте между 12 и 1 ч дня. Пришедший первым ждёт второго ¼ часа, после чего уходит. Найти вероятность того, что встреча состоится, если между 12 и 1 ч дня каждый студент наудачу выбирает момент своего прихода.
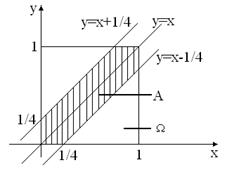
 Пусть x– момент прихода первого студента (необязательно, чтобы он пришёл первым), а y – момент прихода второго. Тогда Ω={(x,y)| x,y
Пусть x– момент прихода первого студента (необязательно, чтобы он пришёл первым), а y – момент прихода второго. Тогда Ω={(x,y)| x,y 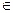 [0,1]}, А=={(x,y)| |x-y|
[0,1]}, А=={(x,y)| |x-y| 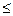
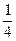 }.
}.
1) x 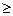 y, x - y =
y, x - y = 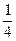 , y = x -
, y = x - 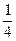 ;
;
2) x<y, y - x = 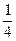 , y = x +
, y = x + 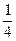 ;
;
P(A)= 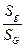 =1-
=1- 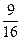 =
= 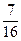
Дата добавления: 2015-06-17; просмотров: 994;
