Модели ректоров с неидеальной структурой потока

В теории реакторов разработаны модели, позволяющие учесть неидеальность потока. Эти модели тоже являются приближенными, однако они более точно описывают реальный процесс, чем модели идеального смешения или вытеснения.

Математические модели реальных реакторов могут быть построены на основе двух подходов.

1) Основан на мысленной замене реального реактора той или иной комбинацией идеальных аппаратов.

2) При составлении математического описания стремятся учесть все реальные физические явления, происходящие в аппарате и внести их в уравнение модели.

При первом подходе математическая модель представляет собой систему уравнений, объединяющих математические описания нескольких идеальных реаторов. Число уравнений может быть велико, но по структуре они остаются такими же простыми, как и уравнения идеальных моделей.

При втором подходе число уравнений может быть меньше, но они более сложные и следовательно сложные методы их решения.

Большинство производственных реакторов работает в режиме ча­стичного или локального перемешивания реагентов с продуктами реакции, т. е. реальный реактор занимает некоторое промежуточ­ное положение между реакторами полного смешения и идеального вытеснения. Такие реакторы достаточно точно описываются так на­зываемой диффузионной моделью.

Диффузионная модель. Эта модель математически выражается уравнениями, в которых учтено изменение концентрации не только вследствие химического превращения (как при идеальном вытес­нении), но и в результате некоторого перемешивания реагентов и продуктов реакции за счет молекулярной или турбулентной диффу­зии. Диффузионная модель может быть описана моделью идеаль­ного вытеснения с введением членов, учитывающих соответствую­щее перемешивание фаз в реальном аппарате.

Радиальное перемешивание сглаживает температурные и кон­центрационные поля в горизонтальном (элементарном) слое и вы­равнивает время пребывания отдельных частиц. Таким образом, ра­диальное перемешивание всегда полезно и оно мало влияет на мо­дель реактора. Поэтому уравнение диффузионной модели обычно записывают в однопараметрическом виде, учитывая только про­дольный перенос. Для необратимой химической реакции п-го по­рядка при установившемся (стационарном) режиме оно имеет вид

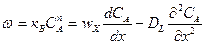
где D_L— коэффициент продольного перемешивания, равный эффек­тивному коэффициенту диффузии.

Его удобно представить в безразмер­ном виде, введя новую переменную l—x/L, где L— длина реактора., тогда x=lL, dx = Ldl. С учетом соотношения

L/ω, 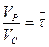и выражения 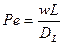где Ре – диффузионный критерий Пекле

в безразмерном виде уравнение запишется как

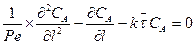
Уравнение решается с определенными граничными усло­виями и, как правило, с использованием ЭВМ. Оно охватывает весь диапазон реальных реакторов, работающих без застойных зон и байпасирования реагентов. Если Ре = 0 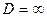, уравнение преобразуется в модель полного смешения; при 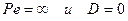— в модель идеального вытеснения.

Для реакции первого порядка решение дифференциального уравнения дает следу­ющий результат:

,

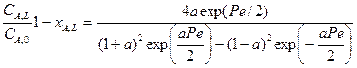где

Характер изменения степени пре­вращения по высоте реактора при различных числах Пекле (рис. 1) подтверждает это положение.

Рис.1. Зависимость изменения степени превращения вещества х по высоте изотермического реакто­ра при различных значениях кри­терия Ре

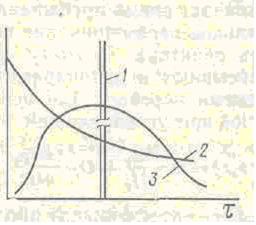
Рис.2 . Кривые отклика на импульсное возмущение в реакторах различного типа:

1 — идеального вытеснения; 2 — полного смеше­ния; 3 — произвольного режима

Вывод функций распределения времени пребывания для реакторов, описываемых однопараметрической диффузионной моделью основан на расчете концентрации индикатора на выходе из реак­тора. Для этого необходимо решить дифференциальное уравнение диффузионной модели в нестационарном режиме без учета химиче­ской реакции