Service Properties Defined from Tests

The properties of a transformer operating under load can be defined from the tests directly conducted on it. If we cause the transformer to carry a load and then change the load amount, the meter readings will indicate the changes both in voltage across the secondary ter­minals and transformer efficiency. But full-load tests result in a large consumption of power, which grows with the size of a trans­former, and call for cumbersome devices such as rheostats, induc­tors, and capacitors needed to specify its performance at resistive, inductive, and capacitive loads. Besides, the direct tests on loaded transformers give very inaccurate results.

Operating characteristics of a transformer can be estimated from the data obtained in short-circuit and open-circuit tests. These tests call for a small amount of power, eliminate the need for bulky equipment, and provide much more accurate measurement results than direct tests.

The open-circuit test uses the meters which indicate the primary and secondary voltages, V₁ and V₂, open-circuit current I₀, and power input P₀ absorbed in the core to compensate for the core loss, i.e. P₀ = P_c.

In the short-circuit test the measured quantities include the short-circuit voltage V_sc, primary current equal to the rated current, power P_sc received by the transformer to offset the copper loss in the wind­ings at the rated load, i.e. P_sc = P_w, resistance R_sc, reactance X_sc, and impedance Z_sc of the short-circuited transformer, and also the percentages of impedance voltage v_sc, and its active component v_a and reactive component v_x.

The data obtained from short-circuit and open-circuit tests allow us to estimate the secondary voltage and transformer efficiency at any load.

The percentage drop of the secondary voltage at any load is dv = [(V₂₀ — V₂)/V₂₀] x 100 = β (v_a cos φ₂ + v_sc sin φ₂), where β = I/Ii is the load factor, I is the current at the given load, and φ₂ is the phase shift between the secondary voltage and current.

The secondary load voltage is V₂ = V₂₀ (1 — dv/100), where V₂₀ is the open-circuit voltage.

Thus, the secondary voltage depends both on the magnitude and the load character.

Where the load is inductive in character, the voltage decreases with an increased load, and to a greater extent than when the trans­former carries a purely resistive load. At a capacitive load, the voltage grows with the load. Specifying the values of β and φ₂, we can determine dv and V₂ at any load carried by the transformer without subjecting it to load tests.

The efficiency of a transformer is the ratio of the power output P₂ to the power input P₁ supplied by a power source, η= P₂/P₁. The input P₁ is always higher than the output P₂ because a certain amount of energy destined for transformation is lost as heat. The total power losses are equal to the sum of the core loss P_c and copper loss in the windings. P_w. So, the power input can be defined as P₁ = P₂+P_C + P_w.

The useful power taken off a single-phase transformer is P₂ == F₂I₂ cos φ₂ and that supplied by a three-phase transformer is P₂ = 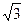V₂I₂ cosφ₂.

Consequently, the efficiency of a single-phase and a three-phase transformer can be written as

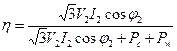
The efficiency of a transformer is the highest at the load for which the core loss is equal to the copper loss. The percentage efficiency of modern transformers is very high and reaches 95 to 99.5%.

Given the values of power input and power output, it is possible to estimate the power losses in the transformer at each specified value of the output.

The core losses in a transformer depend on the grade of steel used for the core, the current frequency, and on the flux density in the core. As the frequency and the flux density remain invariable during transformer operation, the core losses are also independent of the load and remain invariable.

The copper losses I²R are load losses in the windings, which appear as heat when current flows in conductors. They are proportional to the square of the load current. Thus, at half load the currents in the winding will be equal to one half the rated value and load losses to one fourth the losses at full load. Specifying the values of φ₂, we can estimate the transformer efficiency at any load.