Autotransformers

The autotransformer is a device in which parts of one winding are common to both the primary and the secondary made from conductors of a different cross section and wound on the common

steel core. In a step-down autotransformer, for example, the two windings electrically connected in series form a common HV wind­ing. One of the two windings that is a part of the HV winding serves as a LV winding. So, unlike an ordinary transformer, an auto­transformer has both inductive and conductive coupling between its windings.

The circuit diagram of a step-down autotransformer is shown in Fig. 6.7. As seen, the primary (HV) winding comprises all the w₁ turns between the terminals A and X, and the secondary (LV) winding has w₂ turns between the tap and terminal X.

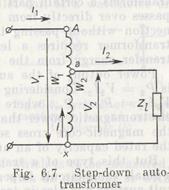At no-load, when I₂=0, if the voltage drop across the primary impedance is left out of consideration, the equilibrium emf equations for the primary and second­ary can be written in the form: V₁ = E₁ = 4.44w₁fΦ_m and V₂ = E₂ = 4.44w₂fΦ_m. The transformation ratio here is V_1/V₂ = w₁/w₂ = n.

If the secondary supplies a certain load, the current I₂ flows in the second­ary circuit. Neglecting the energy loss, the power drawn by the autotransformer from the supply circuit can be taken equal to the power delivered to the secondary circuit, P = V₁I₁ = V₂I₂. whence I₁/I₂ = w₂!w_x=1/n.

Thus, the basic relations for an ordinary transformer are also valid for an autotransformer.

In the common section a-X, the primary current I₁ and the second­ary current I₂ flow in opposite directions. If we disregard the open-circuit current whose value is very small, we may assume that the currents I₁ and I₂ are out of phase by 180° and the current I₁₂ in the common section a-X is equal to the difference between I₂ and I₁: I₁₂ = I₂ - I₁ =I/₂ (1 – 1/n).

In a step-down autotransformer the current I₁₂ flows in the same direction as I₂. In a step-up autotransformer, I₁₂ is opposite in direction to I₂.

The advantages of the autotransformer over an ordinary trans­former of the same capacity are a smaller amount of the winding wire and steel used, a lower power loss, a higher efficiency, and a lower variations in voltage with changes of the load on the device.

The autotransformer requires a smaller mass of wire than an ordinary transformer of the same capacity that carries current of the same density. The thing is that the latter has two windings of which the primary comprises w₂ turns of wire of one cross section and the secondary w₂ turns of wire of another cross section for the current I₁ and I₂ respectively. The autotransformer also has two

windings A–a and a–X, the conductors of which differ in cross section. But the first winding comprises w₁ – w₂ turns of wire designed for current I₁ and the second consists of w₂ turns of wire intended to carry the current difference I₁₂ = I₂ – I₁.

The core of the autotransformer is also smaller in cross section and mass than that of an ordinary transformer. What accounts for this fact is that the latter transforms energy from the primary to the secondary due to electromagnetic induction. The former actually transforms a certain part of the energy output; the remaining part passes over directly from the primary by way of an electrical con­nection without passing through the secondary. Hence, the auto­transformer requires a less amount of electromagnetic power to transfer energy from the primary to the secondary.

Power output of the autotransformer supplying a resistive load is P₂ = V₂I₂. Considering that I₂ = I₁ +I/₁₂, we get P₂ = V₂I₁ + V₂I₁₂ = P_e + P_m, where P_e is the electric power and P_m is the electromagnetic power that determines the required magnetic flux, the magnetic-core cross section, and its mass. This power P_m is the rated capacity of an autotransformer.

But this type of a transformer presents substantial drawbacks: a small short-circuit impedance which results in a heavy short-cir­cuit current and also in transformation of energies that only slightly differ in voltages because the high voltage difference between the electrically connected primary and the secondary renders this device unsafe. The electrical connection also makes it impossible to employ the autotransformer to supply power to a load with a grounded pole, such as a rectifier unit.

The merits of an autotransformer show up more vividly when it operates at a transformation ratio n as close to unity as possible. This explains why this device is used to transform energy at n = 1 to 2.

Three-phase autotransformers employed in three-phase networks usually have their windings connected in star.