Временной анализ линеаризованных цепей

Важным следствием линеаризации является то, что анализ реакции цепи на приращения относительно режима покоя - это задача при нулевых начальных условиях.

При нулевых начальных условиях применение одностороннего преобразования Лапласа

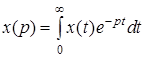
приводит к замене операции дифференцирования и интегрирования по времени к операции умножения или деления на переменную р:

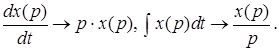(2.12)

В результате дифференциальное уравнение, определяющее связь “вход-выход” цепи, трансформируется в алгебраическое в функции от р:

y(p)=x(p)·K(p), (2.13)

где 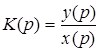- передаточная функция цепи.

Переход от изображения реакции цепи к оригиналу (обратному преобразованию Лапласа L^-1[у(р)] ) может быть проведен на основании интеграла свертки.

В теории преобразования Лапласа доказано, что, если y(p)=A(p)·B(p), а A(t), B(t) - оригиналы А(р) и В(р),

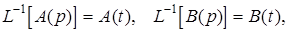
то имеет место равенство, которое и называется интегралом свертки

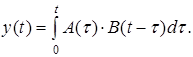(2.14)

На основании интеграла свертки можно, зная реакцию цепи на некоторый тестовый сигнал, определить реакцию цепи на любой сигнал. В качестве тестового сигнала может, например, выступать дельта-функция d (t) - импульс бесконечно большой амплитуды и бесконечно малой длительности. По определению дельта-функции площадь под кривой d (t) равна единице:

.

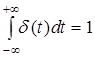Хотя дельта-функция является математической абстракцией, ее введение позволяет во многих случаях упростить анализ.

Поскольку изображение по Лапласу дельта-функции

,

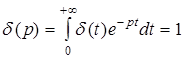то реакция цепи на дельта-функцию есть оригинал передаточной функции и называется импульсной характеристикой цепи:

K(t)=L^-1[K(p)].

Для произвольного сигнала x(t) имеем

y(p)=x(p)·K(p)

и на основании (2.14) получим

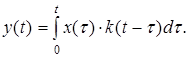(2.15)

Соотношение (2.15.) означает, что, зная импульсную характеристику цепи k(t), можно определить реакцию цепи на любой сигнал x(t).

Реакция цепи на единичное ступенчатое воздействие x(t)=1=1(t)(t³0) называется переходной характеристикой цепи h(t).

Поскольку изображение по Лапласу единичной функции

,

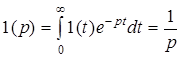то реакция системы на единичное воздействие будет равна

h(p)=1(p)·K(p) = ,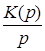

тогда переходная характеристика

.

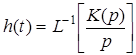Для произвольного сигнала x(t) реакция цепи

y(p)=x(p)·K(p).

Проведем очевидное преобразование этого выражения:

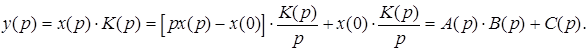
На основании свойств преобразования Лапласа оригиналы

.

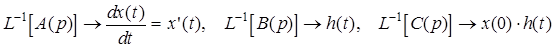Тогда на основании интеграла свертки и свойства линейности преобразования Лапласа получим

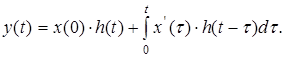(2.16)

Соотношение (2.16.) называется интегралом Дюамеля и позволяет по известной переходной характеристике цепи h(t) определить реакцию на любой сигнал.