Донорная примесь

Материал этой примеси выбирается таким, чтобы разрешенные уровни ее электронов находились вблизи “дна” зоны проводимости (рис. 3.2). За счет значительно меньшего удаления от зоны проводимости вероятность перехода электронов примеси в зону проводимости уже при комнатной температуре резко увеличивается по сравнению с электронами валентной зоны (см. пунктир). Свободные носители в зоне проводимости в основном будут обусловлены электронами примеси, а их число намного больше дырок в валентной зоне. Такой полупроводник называется электронным, или п-типа. Электроны называются основными носителями, а дырки - неосновными, причем имеет место неравенство

n_n >> p_n. (3.3)

Рис. 3.2. Донорная примесь

В отличие от электронов, уходящих из валентной зоны, электроны примеси, перешедшие в зону проводимости, дырок не образуют, поскольку при малой концентрации примеси расстояние между ее атомами настолько велико, что переход электрона от одного атома примеси на освободившийся уровень у другого атома становится невозможным, поэтому атом примеси, потерявший электрон, становится положительно заряженным ионом, не способным передвигаться в твердом теле.

Концентрация носителей в примесном полупроводнике подчиняется закону

n_n× p_n=n_i². (3.4)

Соотношение (3.4) означает, что увеличение объема примеси, с одной стороны, приводит к увеличению основных носителей, но, с другой стороны, возрастает и вероятность их рекомбинации, когда электрон из зоны проводимости возвращается на свободные уровни примеси, деионизируя ее атомы. В результате этих процессов и наступает равновесие, определяемое соотношением (3.4).

Поскольку уже при комнатной температуре практически все атомы примеси становятся ионизированными, число основных носителей от температуры практически не зависит (n_n»const).

Согласно соотношению (3.4)

,

а это означает, что число неосновных носителей очень сильно зависит от температуры из-за аналогичной зависимости от температуры числа собственных носителей n_i .

Для того, чтобы оценить сложность технологического процесса введения примеси, рассмотрим следующий пример.

Количество атомов в 1 грамме вещества (число Авогадро) составляет примерно N_i=6× 10²³. Число свободных носителей в собственном полупроводнике равно n_i»2× 10¹⁰ (кремний). Допустим, что введена донорная примесь, число атомов которой составляет 10^-3 % от общего числа атомов исходного полупроводника, то есть N_q = 6× 10²³× 10 ^-5=6× 10¹⁸. Все эти атомы будут ионизированы, что приведет к образованию свободных электронов n_n=6× 10¹⁸. Таким образом, введение одной тысячной процента примеси приведет к увеличению электропроводности в раз!

Очевидно, что для получения исходного чистого полупроводника, управления примесной проводимостью применяются сложнейшие технологии, какими стало обладать человечество лишь во второй половине ХХ века.

При повышении температуры число свободных электронов, образовавшихся при ионизации примеси, остается практически неизменным, а число электронов, переходящих из валентной зоны, как это было и в собственном полупроводнике, экспоненциально нарастает. Поскольку число атомов исходного полупроводника на несколько порядков превышает число атомов примеси, число “собственных” электронов в зоне проводимости становится много больше электронов от примеси. В полупроводнике снова устанавливается практическое равенство свободных электронов и дырок (см. 3.1),: примесный характер проводимости практически исчезает. Такой полупроводник называется вырожденным. Поскольку примесный характер проводимости является для многих приборов главным условием функционирования, критическая температура, при которой происходит вырождение, является важнейшей характеристикой полупроводника, определяющей его температурный “потолок” нормальной работы. Поэтому вместо германия (критическая температура »80°С) в настоящее время в основном используется кремний (более150°С), а также арсенид галлия (более 200°С).

Важное значение в теории электропроводности полупроводника играет такое понятие, как уровень Ферми (j_F).

Уровень Ферми - это сумма химического потенциала, обеспечивающего диффузию носителей в объеме твердого тела и электрического потенциала, обеспечивающего дрейф носителей. Движение носителей (электропроводность) возможно лишь при наличии градиента или химического, или электрического потенциала. В равновесном состоянии, когда направленного движения носителей в твердом теле нет, градиент уровня Ферми равен нулю, то есть j_F=const.

Это значит, что уровень Ферми располагается горизонтально. Уровень Ферми является функцией концентрации свободных носителей

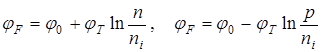, (3.5)

где j₀ - потенциал середины запрещенной зоны.

Для собственного полупроводника, у которого согласно (3.1) n=n_i

j_F = j₀,

то есть уровень Ферми расположен в середине запрещенной зоны.

Для электронного полупроводника согласно (3.3) и (3.4) n_n>n_i и

j_F > j₀,

то есть уровень Ферми перемещается выше середины запрещенной зоны.