Двутавровые и коробчатые сечения.

Двутавровые и коробчатые сечения рассчитываются как тавровые (рис. 44, 45).

Уширения нижней полки условно отбрасываем, поскольку работа растянутого бетона не учитывается.

10.3. Прочность сечения элемента наклонного к
продольной оси.

Опыты показывают, что вблизи опор изгибаемого элемента в результате совместного действия поперечной силы и изгибающего момента могут возникнуть наклонные трещины, причем наклон их зависит от характера армирования элемента, размеров поперечного сечения, прочностных характеристик бетона и арматуры.

Из курса сопротивления материалов известно, что изгибающий момент М вызывает в материале балки нормальные напряжения σ, а поперечная сила Q – касательные (скалывающие) напряжения τ; при этом на наклонных площадках действуют главные растягивающие и главные сжимающие напряжения (рис. 46).

При достижении главными растягивающими напряжениями величины предельного сопротивления бетона растяжению R_bt происходит образование наклонной трещины (стадия I-а) (рис. 36). Части элемента, находящиеся, справа и слева от наклонной трещины стремятся взаимно повернуться вокруг точки, расположенной в сжатой зоне сечения над трещиной. Такому повороту препятствует арматура, пересекаемая наклонной трещиной (продольная арматура, поперечные стержни, отогнутая арматура). После образования трещин напряженно-деформированное состояние соответствует стадии 2. При дальнейшем возрастании нагрузки происходит разрушение элемента по наклонному сечению (стадия 3).

При этом может быть преодолено сопротивление растянутой продольной арматуры или (чаще) нарушена ее анкеровка (причина→изгибающий момент М), или при надежной анкеровке продольной арматуры сдвиг по сечению поперечной силы Q.

В настоящее время отгибы используются главным образом в вязаных каркасах, при строительстве из монолитного железобетона.

Основное армирование наклонных сечений выполняется поперечными стержнями в сварных каркасах.

Условие прочности:

.

()

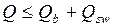Проверка необходимости расчета прочности по наклонному сечению производится из условия:

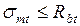, где σ_mt – главные растягивающие напряжения.

.

()

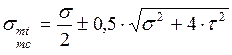Приближенно 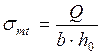, отсюда: 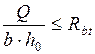, то есть вся поперечная сила воспринимается бетоном без армирования. СНиП предусматривает коэффициент 0,5.

,

()

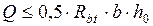при соблюдении этого условия поперечная арматура не рассчитывается, а ставится по конструктивным требованиям.

При 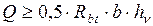- поперечная арматура ставится по расчету.

Конструктивные требования к поперечной арматуре:

1) Диаметр поперечных стержней назначается по условию свариваемости с продольной арматурой;

2) Шаг S_w: при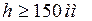

- для арматуры назначаемой по расчету: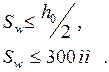

- для арматуры назначаемой конструктивно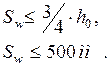

Усилие в поперечных стержнях, пересекаемых, наклонной трещиной:

.

()

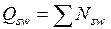Условие прочности:

,

()

,

()

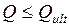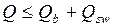где 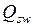- поперечная сила воспринимаемая поперечной арматурой; 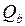- поперечная сила воспринимаемая бетоном в наклонном сечении.

Площадь поперечной арматуры в сечении:

,

()

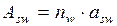где 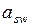- площадь поперечного стержня; 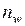- число поперечных стержней в сечении.

Поперечная сила воспринимаемая бетоном в наклонном сечении:

()

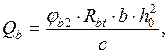
где φ_b2 – коэффициент, принимаемый равным 1,5.

Поперечная сила воспринимаемая поперечной арматурой в наклонном сечении:

.

()

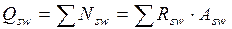Введем понятие 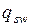- усилие в поперечной арматуре на единицу длины элемента.

;

()

,

()

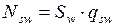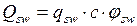где 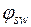- коэффициент, принимаемый равным 0,75.

Уравнение несущей способности сечения по поперечной силе:

()

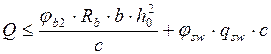
Проекция опасного сечения.

Опасное сечение – это сечение минимальной несущей способности с проекцией с₀.

Для нахождения с₀ необходимо взять первую производную по переменной с от 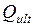и приравнять ее к нулю.

,

()

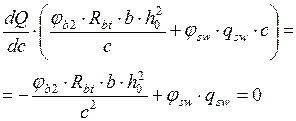отсюда:

()

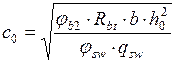
где 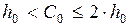; 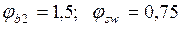- для обычного тяжелого бетона.

.

()

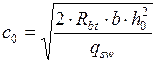При 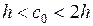принимают ;

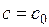при 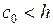принимают ;

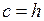при 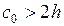принимают .

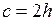Полученную величину проекции наклонного сечения с подставляем в формулу несущей способности сечения и определяем :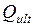

()

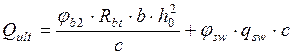
При 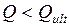- несущая способность не обеспечена, необходима корректировка сечения. Для этого увеличивают диаметр поперечных стержней или уменьшают их шаг.

Порядок расчета:

Известно: .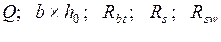

1. Расчет элемента по бетонной полосе между наклонными сечениями

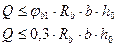.(вывод?)

2. Проверка необходимости расчета поперечной арматуры:

При 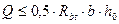- конструктивно;

При 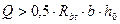- по расчету.

3. Принимаем диаметр и шаг поперечных стержней по конструктивным требованиям:

;

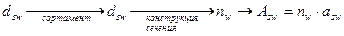- зная ;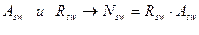

- зная .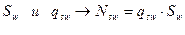

Отсюда: .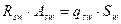

4. Определяем необходимую интенсивность поперечного армирования:

.

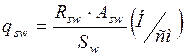5. Определяем С₀:

.

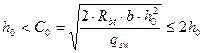6. Устанавливаем несущую способность сечения по общей формуле:

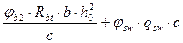и сравниваем с Q.

7. При необходимости проводим корректировку армирования: (увеличение диаметра 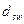и уменьшение шага ).

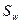10.4. Анкеровка продольной арматуры на опорах и обрыв
арматурных стержней в пролете.

Продольная арматура доводится до опоры полностью (рис. 51,а) или частично обрывается в пролете (рис. 51,б).

В обоих случаях необходимо учитывать следующие конструктивные требования по размещению продольной арматуры:

1) До опоры доводится не менее 30% арматуры, но в каждом углу сечения обязательно должен быть стержень;

2) Продольная арматура доводимая до опоры заводится за грань опоры не менее, чем на 10d ( 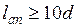) при классах арматура А400 или А500 и не менее, чем на 15d при классе арматуры А300, где d –диаметр продольной арматуры;

3) На длине 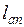должно быть поставлено не менее одного поперечного стержня;

4) Обрыв стержней в пролете выполняется согласно эпюры материалов.

Эпюра материалов – это графическое изображение величины изгибающих моментов внутренних усилии (несущей способности изгибаемого элемента) в каждом сечении по длине его пролета.

В соответствии с уменьшением изгибающего момента часть стержней можно оборвать.

Требуемый размер w должен приниматься не менее 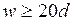, где d – диаметр обрываемо арматуры.

Для построения эпюры материалов вычисляются предельные изгибающие моменты, которые могут быть восприняты сечениями элемента 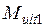и :

()

()

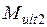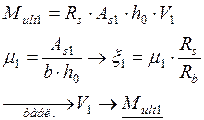
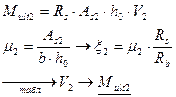
Эпюра моментов – исходный материал для построения эпюры материалов. Она не должна выходить за контуры эпюры материалов.