Контактная разность потенциалов и толщина слоя объемного заряда

Рассмотрим явления в контакте металл – полупроводник при отсутствии поверхностных состояний. Возьмем контакт электронного полупроводника (n-типа ) и металла в предположении, что работа выхода электрона из полупро­водника Ф_П меньше работы выхода электрона из металла Ф_М, то есть Ф_П < Ф_М.

На рисунке 1а показана зонная энергетическая диаграмма металла (Me) и полупроводника (п/п) не находящихся в контакте друг с другом. Термодинамическая работа выхода – это расстояние от уровня вакуума Е₀ до уровня Ферми в металле F_М или в полупроводнике F_М:

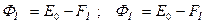. (1)

Если металл и полупроводник привести в непосредственный контакт (рис.1б), то электроны будут переходить преимущественно из полупроводника в металл, так как уровень Ферми в полупроводнике в момент соединения с металлом лежит выше, чем в металле, F_П > F_М. При этом металл заряжается отрицательно, а полупроводник – положительно. Направленный поток электронов проходит над потенциальным барьером, который возникает в приконтактной области полупроводника (рис. 1в). Этот поток электронов будет иметь место до тех пор, пока уровни Ферми F_П и F_М не выровняются, после чего установится динамическое равновесие (токи j_П и j_М будут равны друг другу). Между металлом и полупроводником возникает контактная разность потенциалов:

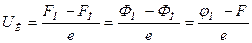, (2)

где е – абсолютная величина заряда электрона.

Здесь при выводе этой формулы разность уровней F_П - F_М берется из рис. 1а или рис. 1б, так как после установления равновесия (рис. 1в) F_П = F_М . Величина j_М – это высота потенциального барьера со стороны металла, она имеет смысл работы выхода электронов из металла в полупроводник, равной расстоянию от уровня Ферми до зоны проводимости на границе. Величина F = E_C – F_П в глубине проводника, рис. 1в. При этом имеет место следующее равенство:

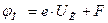. (3)

Итак, в приконтактной области полупроводника возникает слой положи­тельного объемного заряда толщиной L, рис. 1в. Из этого слоя все электроны ушли в металл. В физике полупроводников доказывается, что толщина этого слоя

, (4)

где ε – диэлектрическая проницаемость полупроводника, ε₀ – электрическая постоянная, n₀ – концентрация свободных электронов в глубине полупроводника (т.е. при x > L).

Рис. 1. Зонная энергетическая диаграмма контакта металл – полупроводник (Me – п/п)

а) Me и п/п далеко друг от друга;

б) момент соприкосновения Me и п/п;

в) после установления термодинамического равновесия

Рис. 2. Зонная диаграмма контакта металл-полупроводник

а) при положительном напряжении;

б) при отрицательном напряжении

Величина L обычно составляет 10÷100 нм. Концентрация свободных электронов в металле значительно больше, чем в полупроводнике, поэтому толщина отрицательного слоя объёмного заряда в металле ничтожно мала и она не дает вклада в контактную разность потенциалов. Толщина слоя объёмного заряда L называется длиной экранирования Дебая. Этот слой экранирует внут­реннюю часть полупроводника от проникновения туда контактного поля.

Рассмотрим условие динамического равновесия при контакте металла и полупроводника, рис. 1в. Ток термоэлектронной эмиссии электронов из металла в полупроводник над потенциальным барьером высотой j_М дается уравнением Ричардсона-Дэшмена:

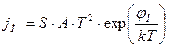, (5)

где А – постоянная, Т – абсолютная температура, k – постоянная Больцмана, S – площадь контакта.

Обратный ток термоэлектронной эмиссии электронов из полупроводника в металл j_П равен, см. рис. 1в:

, (6)

где величина eU_К + F играет роль работы выхода электрона из полупроводника в металл. При динамическом равновесии j_М = j_П. Этот же вывод следует и из уравнения (3).